Министерство образования и науки РФ
ФГБОУ ВПО «Волгоградский государственный технический университет»
Факультет технологии конструкционных материалов
Кафедра «Технология материалов»
Примеры выполнения основных статистических расчетов в металлургии
Методические указания к практическим занятиям работы по специальности 150105.65 «Металловедение
и термическая обработка металлов» и магистерской подготовке
по программе 150100 «Металлургия»
ВОЛГОГРАД
2011
УДК 669.012.2
Р е ц е н з е н т:
канд. техн. наук доцент Приходьков К.В.
Печатается по решению редакционно-издательского совета
Волгоградского государственного технического университета
Примеры выполнения основных статистических расчетов в металлургии: метод. указания к практическим занятиям /Сост. А.В.Крохалев, С.С. Сычева, Е.А. Косова / ВолгГТУ. – Волгоград, 2011. – 16с.
Методические указания содержат примеры статистических расчетов, применяемых в металлургии и последовательность необходимых для их выполнения расчетов и графических построений.
Методические указания к практическим занятиям предназначены для студентов очной и очно-заочной формы обучения специальности 150105 «Металловедение и термическая обработка металлов»
© Волгоградский государственный
технический университет, 2011
Цель занятий
Целью практических занятий является закрепление теоретического материала изученного на лекциях и наработка практических навыков выполнения статистических расчетов, наиболее часто встречающихся при решении задач разработки, исследования и контроля технологических процессов металлургического производства.
Содержание занятий
Изучение существующих методик выполнения статистических расчетов.
Изучение особенностей конкретного расчетного задания и выбор необходимой методики расчета.
Проведение расчета и формулирование выводов.
3. Методика выполнения расчетных заданий
Выданное преподавателем индивидуальное задание записывается в тетради с лекциями. Далее выполняются все необходимые расчеты, причем на каждом этапе расчета сначала приводится расчетная формула с расшифровкой всех входящих в неё величин, а лишь затем производится подстановка в формулу всех необходимых значений из условий задания или из ранее произведенных расчетов, и приводится результат вычислений. Необходимые графические построения проводятся на миллиметровой бумаге, с указанием названия осей и их градуировкой. Масштаб градуировки осей должен обеспечивать достаточную для практики точность определения численных значений статистических величин.
ПРИМЕРЫ СТАТИСТИЧЕСКИХ РАСЧЕТОВ И ПОСЛЕДОВАТЕЛЬНОСТЬ НЕОБХОДИМЫХ ДЛЯ ИХ ВЫПОЛНЕНИЯ РАСЧЕТОВ И ГРАФИЧЕСКИХ ПОСТРОЕНИЙ
4.1 Вычисление среднего, дисперсии и доверительного интервала среднего
Задача: От партии деталей отобрали 5 представителей и замерили их твердость. Результаты измерений приведены в таблице 1. Необходимо определить среднее значение твердости и его доверительный интервал при уровне значимости α=0,05.
Таблица 1 – Результаты измерения твердости
Номер образца |
1 |
2 |
3 |
4 |
5 |
HRC |
45 |
48 |
49 |
47 |
45 |
Решение. Для определения среднего значения твердости и его доверительного интервала при уровне значимости α=0,05 воспользуемся следующей формулой
где
- математическое ожидание;
-
выборочное среднее;
-
выборочная дисперсия;
n - число опытов;
-
табличное значение критерия Стьюдента
(t
- критерия).
Определим выборочное среднее по формуле
,
.
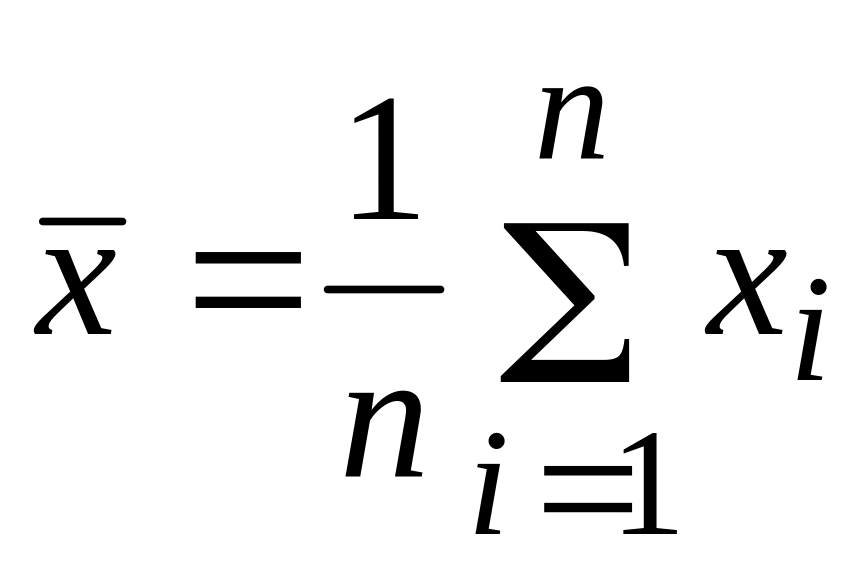Для определения выборочной дисперсии воспользуемся следующей формулой:
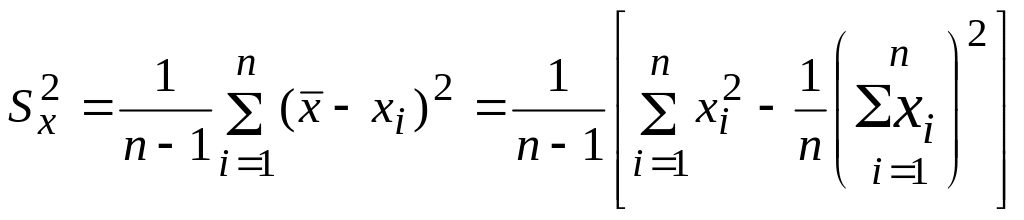
и
для расчета
определим
значения
и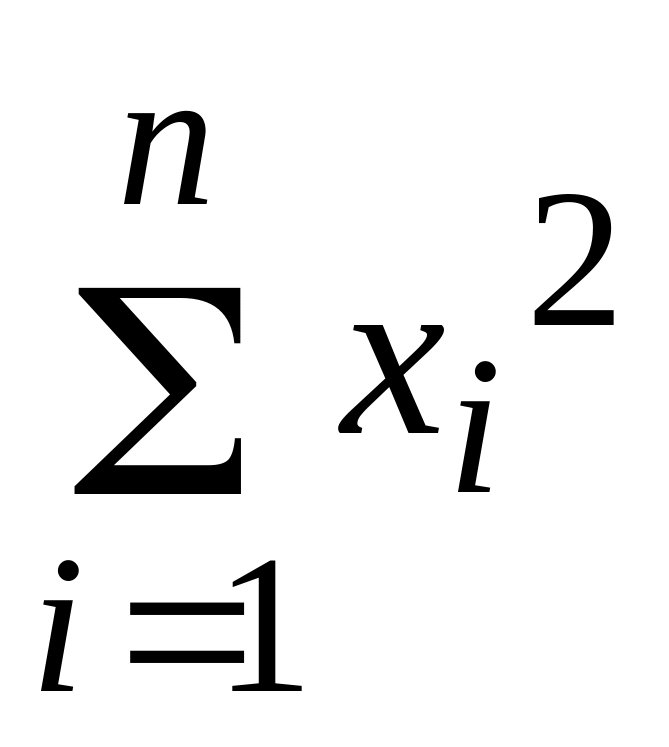
,
сведя расчет в таблицу 2.
Таблица 2 – Результаты расчета
№ опыта |
|
|
1 2 3 4 5 |
45 48 49 47 45 |
2025 2304 2401 2209 2025 |
|
=234 |
=10964 |
Тогда
,
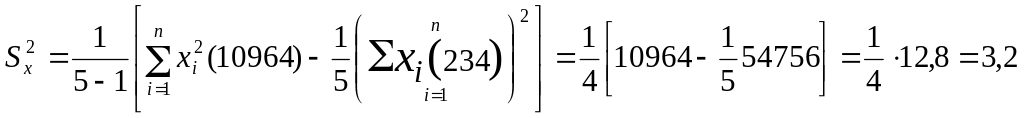отсюда выборочная дисперсия равна
=
=
1,78.
Определим критерий Стьюдента (t - критерий).
,
где f - число степеней свободы
В нашем случае f = n-1=4, тогда по таблице 1 приложения:
Подставив расчетные данные в формулу для вычисления математического ожидания, получим следующее значение
Вывод.
Определили, что среднее значение
твердости (HRC)и
его доверительный интервал при уровне
значимости α=0,05 равно 46,8
2,22.