Вычитание комплексных чисел
Разностью двух комплексных чисел x1 + iy1 и x2 + iy2 называется такое комплексное число, которое будучи сложено с x2 + iy2, даёт в сумме x1 + iy1.
(x1 + iy1) – (x2 + iy2) = (x1 – x2) + i (y1 – y2) (2)
И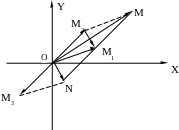
з
формул 1 и 2 следует, что сложение и
вычитание комплексных чисел, изображённых
векторами, производится по правилам
сложения и вычитания векторов.
,
,
,
(x1
+ x2) + i (y1 + y2),
3
= - (x2
+ iy2)
,
,
= (x1
- x2)
+ i (y1
- y2),
=
.
Аналогично, можно показать, что комплексные числа можно умножать на вещественные числа так же, как векторы на скаляры.
Умножение комплексных чисел
Произведением комплексных чисел х1 +iу1 и х2 +iу2 называется такое комплексное число, которое получается при перемножении этих чисел как двучленов по правилам алгебры.
(х1 +iу1)(х2 +iу2) = х1х2 + iх1у2 +iх2у1 + i2у1у2;
(х1 +iу1)(х2 +iу2) = (х1х2 – у1у2) + i(х1у2 + х2у1).
При перемножении сопряженных чисел х1 +iу1 и х2 –iу2 получаем число вещественное:
(х1 +iу1)(х1
–iу1) =
;
(х1 +iу1)(х1
–iу1) =
.
Произведение сопряженных комплексных чисел равно сумме квадратов модулей каждого из них.
Деление комплексных чисел
Деление комплексных чисел определяется как действие обратное умножению:
z1 = х1 +iу1;
z2 = х2 +iу2;
= z3 ; z3
= x3 + iy3.
= x3
+ iy3
; x1 +
iy1 =
(x2 +
iy2)(x3
+ iy3);
x1 + iy1 = (x2 x3 – y2y3) + i(x2y3 + y2x3);
Решая систему уравнений, получим:
x3 =
; y3 =
тогда z3 =
+ i
.
Следовательно, умножив делимое и делитель на число, сопряженное делителю, получим в делителе действительное число. Затем разделим на это действительное число действительную и мнимую части делимого, получим частное.
Для контроля усвоения задать вопрос: Выполнить действия над комплексными числами:.
(2а – 3bi) + (–a – bi) + (4a + 2bi) – (2a – 5bi). Ответ: 3a + 3bi
(5 + 2i)(2 + 3i). Ответ: 4 + 19i
.
Ответ:
Вывод: Комплексные числа, заданные в алгебраической форме, можно складывать, умножать и делить по правилам алгебры действительных чисел, имея в виду значение квадрата мнимой единицы: i2=-1.
2. Умножение и деление комплексных чисел в тригонометрической форме
Над комплексными числами, заданными в тригонометрической форме, рассмотрим следующие действия:
Умножение комплексных чисел
При умножении комплексных чисел, заданных в тригонометрической форме имеем: z1 = r1 (cos 1 + i sin 1) ; z2 = r2 (cos 2 + i sin 2);
z1 z2 = r1 (cos 1 + i sin 1) z2 (cos 2 + i sin 2) =
= r1 r2 (cos 1 cos 2 + + i sin 1 cos 2 + i cos 1 sin 2 + i2 sin 1 sin 2) =
= r1 r2 (cos 1 cos 2 – sin 1 sin 2) + i (sin 1 cos 2 + sin 2 cos 1) =
= r1 r2 cos (1 + 2) + i sin (1 + 2);
z1 z2 = r1 r2 cos (1 + 2) + i sin (1 + 2).
Произведение двух комплексных чисел есть такое комплексное число, модуль которого равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.
Деление комплексных чисел
При делении комплексных чисел, заданных в тригонометрической форме имеем: z1 = r1 (cos 1 + i sin 1); z2 = r2 (cos 2 + i sin 2);
=
= =
=
=
Частное двух комплексных чисел есть такое комплексное число, модуль которого равен частному модулей делимого и делителя, а аргумент частного равен разности аргументов делимого и делителя.
Пример для контроля усвоения: Даны два комплексных числа:
z1 = 6 (cos 450 + i sin 450), z2=2 (cos 150 + i sin 150).
Требуется
найти: z1
z2 и
.
Ответы: z1 z2 = 12 (cos 600 + isin 600); = 3 (cos 300 + i sin 300).
Вывод: Умножение (деление) комплексных чисел в тригонометрической форме сводится к перемножению (делению) их модулей и сложению (вычитанию) аргументов.