Лекции / ЛЕКЦИЯ5_09

5 ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ. ЯВЛЕНИЕ ВЗАИМНОЙ ИНДУКЦИИ.

ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕ ИНДУКТИВНО СВЯЗАННЫХ ЭЛЕМЕНТОВ. МЕТОДЫ РАСЧЁТА ИНДУКТИВНО СВЯЗАННЫХ ЦЕПЕЙ

(Сост. Никонов А.В.)

Фильтры применяются для выделения или подавления определенных коле-

баний, разделения частотных каналов, формирования спектра сигналов. Электри-

ческим фильтром называется четырёхполюсник, пропускающий без ослабления или с малым ослаблением колебания определенных частот и пропускающий с большим ослаблением колебания других частот.

Полоса частот, в которой ослабление мало, называется полосой пропуска-

ния. Полоса частот, в которой ослабление велико, называется полосой непро-

пускания (задерживания). Между этими полосами находится переходная область.

По расположению на шкале частот полосы пропусканияразличают сле-

дующие фильтры:

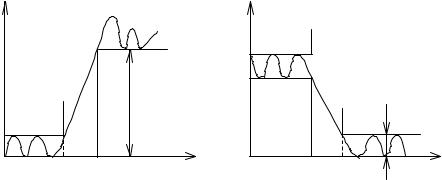
а) нижних частот (ФНЧ), в которых полоса пропускания располагается на шкале частот от ω = 0 до некоторой граничной частоты ω= ωСР, а полоса не-

пропускания (задерживания) – от частоты ω = ωСР до бесконечно больших частот

(рисунок 5.1, а);

Рисунок 5.1 – Электрические фильтры

б) верхних частот (ФВЧ) с полосой пропускания от частоты ω= ωСР до

бесконечно больших частот и полосой непропускания от частоты ω = 0 до ω =

ωСР (рисунок 5.1, б);

д) заграждающие (фильтр-пробка, режекторные), в которых между поло-

сами пропускания 0 – ωСРН и ωСРВ – µ находится полоса непропусканияωСРН –

ωСРВ (рисунок 5.1, д);

е) многополосные, имеющие несколько полос пропускания.

На рисунке 5.1 показаны также условные графические обозначения фильтров каждого типа в соответствии с ГОСТ. В соответствии с используемой элементной

базой к настоящему моменту выделились несколько классов фильтров. Историче-

ски первыми (и все еще наиболее широко применяемыми) являются пассивные фильтры, содержащие элементы L и С. Они носят название LC-фильтров.

Во многих случаях на практике требовалась крайне высокаяизбирательность

(различие ослаблений в полосах пропускания и непропусканияв десятки тысяч раз). Это привело к появлению фильтров с механическими резонаторами: кварце-

вых, магнито-стрикционных, электромеханических.

Самые значительные достижения в области теории и проектирования фильтров связаны с успехами микроэлектроники. Требования микроминиатюризации аппа-

ратуры заставили отказаться от использования индуктивностей, которые

имеют большие габаритные размеры, особенно на низких частотах, и не поддаются исполнению в микроминиатюрном виде. Появились активные RС-фильтры, со-

стоящие из резисторов, конденсаторов и активных приборов(например, транзи-

сторов). Эти фильтры могут быть выполнены в виде микромодульной конструкции или интегральной схемы. Применение активных RС-фильтров ограничивается пока сравнительно небольшим диапазоном частот до нескольких мегагерц.

Разработка цифровых систем и достижения в области цифровых вычислитель-

ных машин стимулировали созданиефильтров на базе элементов цифровой и

вычислительной техники – цифровых фильтров.

ТРЕБОВАНИЯ К ЭЛЕКТРИЧЕСКИМ ХАРАКТЕРИС

ФИЛЬТРОВ. Избирательность фильтра (степень разграничения полос пропус-

кания и непропускания) определяется крутизной характеристики рабочего ос-

лабления. Чем больше крутизна этой характеристики и чем сильнее ослабление в полосе пропускания, тем лучше избирательность фильтра и, следовательно, меньше уровень помех от подавляемых колебаний.

Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик:

а) рабочее ослабление в полосе пропусканияне должно превышать некото-

рого максимального допустимого значенияАP MAX, а в полосе непропускания не

должно быть ниже некоторого минимально допустимого значенияАP MIN. Изо-

бражение этих требований графически показанона рисунке 5.2, а. На этом рисунке

wСР и wЗ – граничные частоты полос пропускания и непропускания.

б) фазочастотная характеристика фильтра (допустимые отклонения от ли-

нейного закона);

в) нелинейные искажения(обусловленные, например, наличием магнитного сердечника в катушках индуктивности).

Могут предъявляться требования и к другим характеристикам и параметрам фильтра.

Идеальные частотные характеристики фильтра заведомо нереализуем. ы

Частотные характеристики реальных фильтров могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра.

Перед тем как перейти к конкретным электрическим фильтрам, необходимо сделать два замечания.

Во-первых, в теории фильтровпринято иметь дело не с обычной угловой частотой w, а с нормированной частотой Ω = w/wН,

где wН – нормирующая частота. Обычно в качестве нормирующей частоты вы-

бирают граничную частоту полосы пропусканияwСР, так что Ω = wСР /wН = wСР

/wСР = 1 .

Во-вторых, имеет смысл подробно изучать только фильтры нижних час-

тот, так как остальные типы фильтров (верхних частот, полосовые и заграждаю-

щие) могут быть легко получены из ФНЧс помощью замены переменной (часто-

ты) или, как принято говорить, с помощью преобразования частоты.

Фильтры типа k и m. Фильтром типа k называются лестничные схемы с

Рисунок 5.3 – Фильтр типа k (Г-образная схема)

Характеристика собственного ослабления А фильтра (рисунок 5.3,6) равна нулю в диапазоне

с

частот 0≤Ω≤1 и монотонно растет по закону Ас= ArchΩ при изменении частоты от 1 до ¥ . Характери-

стические сопротивления фильтра и в полосе пропускания являются активными, но изменяются с ростом частоты по законам (рисунок 5.3, в):

Из двух Г-образных фильтров можно образовать симметричные Т-

образные и П-образные фильтры.

Фильтры типа k обладают двумя существенными недостатками.

Во-первых, они имеют малую крутизну характеристики ослабления АС, что требует использования при построении реальных фильтров очень большого числа Г-

, Т- или П-образных схем.

Во-вторых, частотная зависимость характеристических сопротивлений в

полосе пропускания не позволяет удовлетворительно согласовать фильтр с на-

грузкой и генератором. Это приводит к потерям энергии за счет ее отражения и, как следствие, рабочее ослабление фильтра в полосе пропускания значительно отлича-

ется от нуля, особенно на краях полосы пропускания, где рассогласование наиболь-

шее.

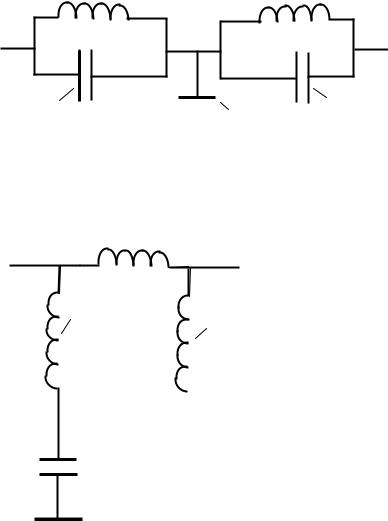
Чтобы избежать этих недостатков, используют фильтры типа т (рисунок

5.4), которые дают всплески ослабленияАС на частоте резонанса контуровWµ.

Своё название фильтры получили из-за того, что значения элементов фильтра типа

m определяются значениями фильтра типаk и параметра m = W ¥2 - 1 / W¥ .

Фильтры типа m:

а) обладают меньшей частотной зависимостью характеристических сопро-

тивлений в полосе пропускания, и

б) лучше согласуются с генератором и нагрузкой.

Wµ Wµ

2mL

Рисунок 5.4 – Фильтры типа m

Но фильтры типа т:

в) имеют в полосе непропускания глубокий спад ослабления АС.

Обычно используют каскадное соединение фильтров типат и k. Фильтры типа k увеличивают ослабление в полосе непропускания, а фильтры типат поднимают крутизну характеристики ослабления вблизи частоты среза.

Ввиду того, что фильтры типа т лучше согласуются с генератором и на-

грузкой, их ставят по краям, а звенья типа k – в середине составного фильтра.

5.1 ЯВЛЕНИЕ ВЗАИМНОЙ ИНДУКЦИИ

При протекании тока i1 (рисунок 5.5) в катушке индуктивности L1 в окру-

жающем пространстве, согласно закону электромагнитной индукции, создается

магнитный поток Ф11.

Рисунок 5.5 – Магнитная связь катушек индуктивности

Если какая-либо часть этого потокаФ12 пронизывает витки другой ка-

тушки с L2, то в последней наводится ЭДС взаимной индукци,иопределяемая законом Максвелла-Фарадея:

где М12 – коэффициент взаимной индуктивности катушек L1 и L2.

Единица измерения взаимной индуктивности – Генри (Гн).

Знак «–» в уравнении () определяется согласно правилу Ленца направлением индукционного тока, который имеет такую ориентацию, чтобы создаваемый им магнитный поток препятствовал тому изменению магнитного потока Ф12, ко-

торое этот ток вызывает.

Напряжение взаимоиндукции на зажимах катушки индуктивности L2:

Если напряжение u приложено к катушке индуктивности L1, то под дейст-

вием тока i2 в катушке L1 также будет наведена ЭДС взаимной индукции:

В соответствии с принципом взаимности для линейных цепей М12 = М21.

Рассмотренная выше индуктивная связь носит односторонний характ:ер

ток i1 вызывает ЭДС взаимоиндукции еМ2 или ток i2 вызывает ЭДС eM1. (В слу-

чае замыкания катушки L2 на конечное сопротивление R (рисунок 5.5) в последней под воздействием uМ2 потечет индукционный ток i2, который, в свою очередь, вызо-

вет в первой катушке L1 ЭДС взаимоиндукции еМ1.)

Таким образом, установится двухсторонняя индуктивная связь катушек

L1 и L2. При этом каждая из катушек L1, и L2 будет пронизываться двумя маг-

нитными потоками: самоиндукции, вызванным собственным током, и взаи-

моиндукции, вызванным током другой катушки.

Следовательно, в катушке L1 индуцируется ЭДС

а в катушке L2 ЭДС:

Взаимное направление потоков само- и взаимоиндукции зависит как от на-

правления токов в катушках, так и от их взаимного расположени.яСледова-

тельно, для определения вида включенияL1 и L2 на схеме достаточно опреде-

То есть, если катушки включаются таким образом, что потоки само- и

Если же потоки само- и взаимоиндукции вычитаются, то такое включение

принято называть встречным.

Рисунок 5.6 – Согласное и встречное включение катушек индуктивности

характеризуют одностороннюю связь между катушками L1 и L2.

Магнитные потоки Ф12, Ф21, Ф11 и Ф22 можно выразить через параметры катушек L1 и L2, М12, М21 и токи il, i2 с помощью формул:

Φ11 = L1i1/w1; Φ12 = M12i1/w 2 ; Φ21 = M21i2 /w1; Φ22 = L2i2 /w 2 , ()

где w1, w2 – число витков катушек L1 и L2 соответственно.

После подстановки данных формул в предыдущие, получим для коэффици-

ента связи:

k = M/L1L2 , ()

где М12 = М21 = М.

Значение k изменяется в пределах от 0 (отсутствие связи) до 1 (сильная связь).