Лекции / ЛЕКЦИЯ3_09

ЛЕКЦИЯ 3. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА. БАЛАНС МОЩНОСТИ. ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИ. ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ В ПАССИВНЫХ ЦЕПЯХ

(Сост. Никонов А.В.)

3.1 Метод эквивалентного генератора

Метод эквивалентного генератора используется в случае, когда необходимо

найти ток, напряжение или мощность в одной ветви.

При этом удобно всю остальную часть цепи, к которой подключена данная

ветвь, рассматривать в виде двухполюсника.

Двухполюсник называют активным, если он содержит источники элек-

трической энергии, и пассивным – в противном случае. На рисунках активный

двухполюсник обозначен буквой А, а пассивный – П.

Различают две модификации метода эквивалентного генератора: МЕТОД ЭКВИВАЛЕНТНОГО ИСТОЧНИКА НАПРЯЖЕНИЯи МЕТОД ЭКВИВАЛЕНТНОГО ИСТОЧНИКА ТОКА.

Метод эквивалентного источника напряжения. Этот метод базируется на

теореме Тевенина, согласно которой ток в любой ветви линейнойэлектриче-

ской цепи не изменится, если активный двухполюсник, к которому подклю-

чена данная ветвь, заменить эквивалентным источником (генератором) на-

пряжения с задающими напряжением, равным напряжению холостого хода на зажимах разомкнутой ветви, и внутренним сопротивлением, равным эквива-

лентному входному сопротивлению пассивного двухполюсникасо стороны

разомкнутой ветви (рисунок 3.1).

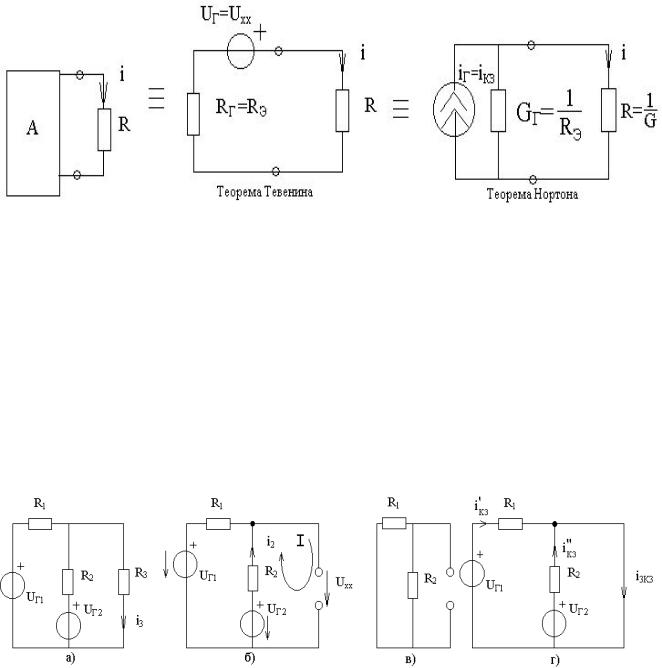
Рисунок 3.1 – Суть теорем Тевенина и Нортона

После замены активного двухполюсника эквивалентным источником на ри-

сунке 3.1, в соответствии с этой схемой имеем:

где RЭ – можно найти либо экспериментальным, либо расчетным путем.

Пример. Найти ток в сопротивленииR3 (рисунок 3.2а) методом эквивалентного источ-

ника напряжения.

Рисунок 3.2 – Применение метода эквивалентного источника напряжения Разомкнем ветвь с R3 и определим uхх по ЗНК для 1-го контура:

а) uхх + R2i2 – uг2 = 0. Отсюда uхх = uг2 – R2i2, где i2 = (uг2 – uг1)/(R1 + R2).

б) Эквивалентное сопротивление RЭ пассивного двухполюсника определяется из схемы на рисунке 3.2в: RЭ = R1R2/(R1 + R2).

в) Подставив uхх и RЭ в уравнение для i, найдем: i3 = uхх/(R3 + RЭ).

Метод эквивалентного источника тока. В основе этого метода лежиттео-

рема Нортона, согласно которой ток в любой ветви линейнойэлектрической

цепи не изменится, если активный двухполюсник, к которому подключена данная ветвь, заменить эквивалентным источником тока с задающим током,

равным току короткого замыкания этой ветви, и внутренней проводимостью,

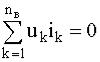
равной эквивалентной входной проводимости со стороны разомкнутой ветви

(см. рисунок 3.1).

Пример. Найти ток в резистивном элементеR3 (рисунок 3.2а) методом эквивалентного источника тока.

Замкнем ветвь с R3 (рисунок 3.2 г) и найдем ток i3кз, методом наложения: i3кз = i'3кз + i''3кз = uг1/R1 + uг2/R2 .

Эквивалентную проводимость определим согласно схеме на рис. 3.2в: Gэ = 1/R1 + 1/R2 = (R1 + R2)/R1R2 = 1/Rэ .

Подставив значения Rэ и i3кз в выражение для i, получим искомое значение тока i3.

Очевидно, что методы эквивалентного источника как напряжения, так и тока, дают один и тот же результат. Применение того или иного метода оп-

ределяется удобством и простотой нахождения uХХ или iКЗ.

3.2 Баланс мощности

Одной из наиболее общих теорем теории электрических цепей являетсятео-

рема Телледжена. Рассматривая произвольную электрическую цепь, содержа-

щую nВ ветвей и nУ узлов, для согласованных направлений напряжений и токов ветвей теорема Телледжена гласит: сумма произведений напряжений uК и то-

ков iК всех ветвей цепи, удовлетворяющих законам Кирхгофа, равна нулю:

Поскольку теорема Телледжена следует непосредственно из законов Кирх-

гофа, то она справедлива для любых электрических цепей: линейных и нели-

нейных, активных и пассивных, цепей – параметры которых изменяются во

времени (параметрических цепей).

Из теоремы Телледжена вытекает ряд следствий, важнейшим из которых яв-

ляется БАЛАНС МОЩНОСТИ. Так какпроизведение uКiК представляет собой

БАЛАНС МОЩНОСТИ можно сформулировать следующим образом: сумма мощностей, отдаваемых независимыми источниками, равняется сумме мощностей, потребляемых остальными ветвями электрической цепи.

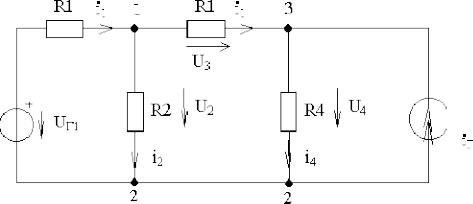
Пример. Составить баланс мощности для цепи, изображенной на рисунке 3.3.

Рисунок 3.3 – Иллюстрация к составлению баланса мощности

1Сумма мощностей, развиваемых источниками напряжения и тока Рист = uг1i1 + u32iг.

2Потребляемая мощность с учетом закона Ома: Рпот = u1i1 + u2i2 + u3i3 + u4i4 = R1i2 +

+R2i22 + R3i32 + R4i42. В соответствии с балансом мощностей Рист = Рпот.

При определении Рист произведение uГi берется со знаком «+», если направ-

ления задающего напряжения uГ и тока i направлены навстречу друг другу, и со знаком «–» в противном случае. Аналогичное правило знаков для источников то-

ка: если напряжение на зажимах источника направлено навстречу задающему то-

ку iГ берется знак «+», а если напряжение совпадает с током – знак «–».

Баланс мощности выражает не что иное, как закон сохранения энергии в электрической цепи.

Одной из важнейших практических задач является оптимальная передача

электрической энергии от активного к пассивному двухполюснику. Оптимум

обычно понимается в смысле получения максимальной мощности в нагрузке

RН.

Для цепи постоянного токаактивный и пассивный двухполюсники можно

заменить эквивалентной схемой, изображенной на рисунке 3.4.

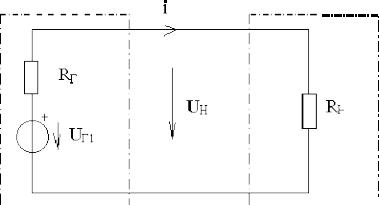
Рисунок 3.4 – Активный и пассивный двухполюсники

Мощность p определим:

Напряжение на нагрузке uН = uГ – iRГ.

Максимум мощности будет достигаться при RН = RГ, при этом ток в цепи принимает значение iО = uГ/(2RГ), а мощность рН max = uГ2/(4RГ).

Коэффициент полезного действия системы передачи определяется равенст-

вом:

При i = iО и pН = pН max имеем h =0,5 (50 %). На рисунке 3.5 представлены зависимости рИСТ, рН и h от тока i.

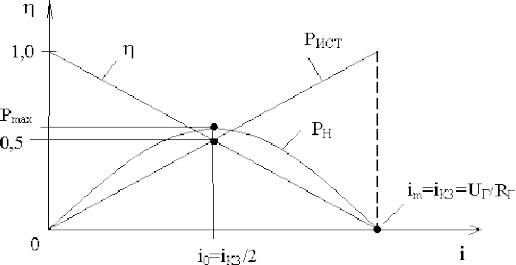
Рисунок 3.5 – Зависимости мощностей, выделяющихся на источнике и на-

грузке при RН = RГ

3.3 ПРЕДСТАВЛЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ

Электрические цепи могут находиться под воздействиемпостоянных или

переменных напряжений и токов. Среди этих воздействий важнейшую роль иг-

рают гармонические колебания.

Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного

сигнала.

Исследование режима гармонических колебаний важно си методической точки зрения, поскольку анализ электрических цепей при негармонических

воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармониче-

ских воздействиях можно распространить и на цепи при периодических несину-

соидальных, а также непериодических воздействиях.

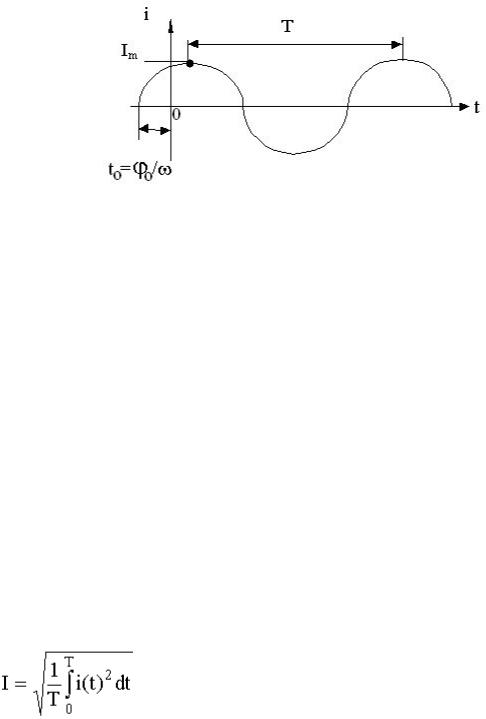
Гармоническое колебание i(t) (рисунок 3.6) характеризуется следующими

основными параметрами:

–амплитудой Im;

–угловой частотой w = 2pf;

–начальной фазой j0.

Начальная фаза j0 = wt0 так как (или t0 = j0/w).

Рисунок 3.6 – Гармонический сигнал

Аналитически гармонические колебания можно определить уравнением:

Для питания различных электроэнергетических установок в СССР принята промышленная частота f = 50 Гц. В качестве источников гармонических колеба-

ний промышленной частоты используются электромашинные генераторы различ-

ного типа. Для получения гармонических сигналов более высоких частот обычно используются ламповые и полупроводниковые генераторы.

Важными параметрами гармонических колебаний являются ихдействую-

щее и среднее значения.

Действующее значение гармонического тока:

После интегрирования получим для действующего значения тока:

Аналогично определяется действующее значение напряжения: U » 0,707Um.

Действующие значения токов и напряженийназывают еще их средне-

квадратичными значениями.

Среднее значение гармонического тока:

. ()

Для гармонического тока IСР = 0. Этот результат понятен, если учесть, что урав-

нение определяет площадь, ограниченную кривой i(t) за период Т.

Гармонические колебания можно представить различными способами:

–функциями времени (временные диаграммы);

–вращающимися векторами (векторные диаграммы);

–комплексными числами;

–амплитудными и фазовыми спектрами.

Тот или иной способ представления применяется в зависимости от характера решаемых задач.

1 ВРЕМЕННОЕ ПРЕДСТАВЛЕНИЕ гармонических колебаний наглядно,

однако его использование в задачах анализа цепей затруднительно, так как тре-

(ИЛЛЮСТРАЦИЯГАРМОНИЧЕСКИХ КОЛЕБАНИЙ).

2 Более удобно ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ гармонических колеба-

ний, при котором каждому колебанию ставится в соответствие вращающий-

ся вектор определенной длины с заданной начальной фазой.

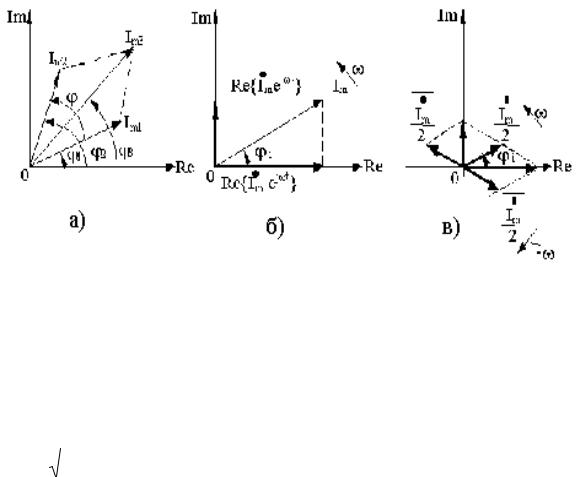
На рисунке 3.7а показано векторное представление двух колебаний i1 и i2:

Рисунок 3.7 – Представление гармонических колебаний

Их сумму i3 можно найти по формулам суммирования векторов:

Величина j = j2 – j1 называется фазовым сдвигом между колебаниями i1 и i2.

Совокупность векторов, изображающих гармонические колебания в электрической цепи, называют ВЕКТОРНОЙ ДИАГРАММОЙ. Векторные диаграммы можно строить как для амплитудных, так и для действующих значе-

ний токов и напряжений.

3 Наиболее распространенными являются представления гармонических ко-

лебаний с помощью КОМПЛЕКСНЫХ ЧИСЕЛ. Эти представления лежат в ос-

нове символического метода расчета электрических цепей – метода комплекс-

ных амплитуд.

Представим ток i на комплексной плоскости. Для этого изобразим вектор

Im на комплексной плоскости с учетом начальной фазы j (рисунок 3.7б).

Будем вращать этот вектор в положительном направлении(против ча-

совой стрелки) с угловой частотой w.

Тогда в любой момент времени положение вращающегося вектора опре-

делится комплексной величиной(комплексным гармоническим колебани-

ем):

Первая часть слагаемого отражает проекцию вращающегося вектора на вещественную ось, а вторая часть – на мнимую ось. Оценив второе слагаемое,

приходим к выводу: синусоидальный ток i на комплексной плоскости пред-

ставляется в форме проекции на мнимую ось вращающегося вектора: