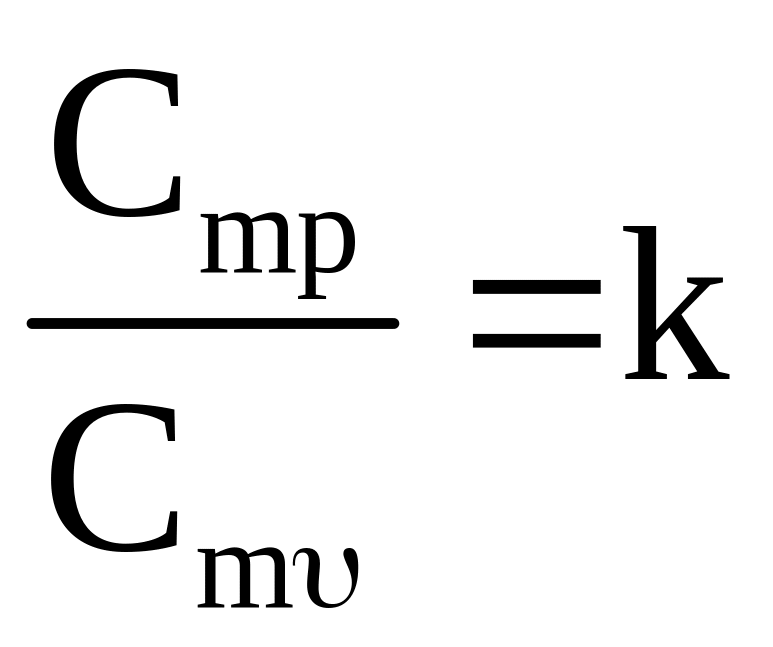Лекція №2. Параметри стану ідеального газу

При термодинамічних розрахунках використовують такі теплові властивості робочих тіл, як :

– теплоємність С, кДж/кг·гр, кДж/нм³ гр, кДж/кмоль·гр;

– теплота q, кДж/кг, ккал/кг;

– робота l, кДж/кг, ккал/кг;

– внутрішня енергія U, кДж/кг, ккал/кг;

– ентальпія i, кДж/кг, ккал/кг;

– ентропія S, кДж/кг гр, ккал/кг·гр;

– теплота випаровування і конденсації r , кДж/кг, ккал/кг;

– теплота згорання палива , кДж/кг, кДж/нм³, ккал/кг, ккал/ нм³.

Усі вказані величини віднесені до 1 кг, або 1 м³ робочого тіла, і тому мають назву питомих характеристик.

Питома середня теплоємність робочого тіла (РТ) – кількість теплоти, що необхідна для зміни температури 1кг (масова) С_m, або 1м³ (об’ємна) , робочого тіла на 1ºС від t₁ до t₂. Залежно від виду термодинамічного процесу, в якому відбувається зміна температури, в розрахунках використовують ізохорну С_mυ, ізобарну С_mр і політропну С_mп теплоємності.

Теплоємність збільшується із підвищенням температури робочого тіла. У зв’язку з цим необхідно розрізняти середню С_m та істинну С теплоємність.

Я кщо величину теплоємності визначають за довідковою літературою як середнє значення у діапазоні зміни температури РТ від t₁ до t₂, наприклад, згідно із залежністю

,

де a i b – довідкові сталі для заданого газу, то визначувана величина С_m є середньою питомою теплоємністю у діапазоні змін температури від t₁ до t₂.

Якщо ж теплоємність визначається при певному значенні температури t робочого тіла за умови, що Δt=t₂– t₁→0, відповідно до довідкових залежностей

C = a + bt + сt²,

то в якості С маємо істинну питому теплоємність. У теплотехнічних розрахунках нелінійні залежності теплоємності від температури з достатньою точністю можна замінити на лінійні виду С = a + b·t, що наведені у довідковій літературі ( додаток А).

Теплоємність ідеальних газів залежить не тільки від їх температури, а й від їх атомності і виду процесу.

Теплоємність реальних газів залежить від виду газу, характеру процесу, температури і тиску.

Технічні розрахунки виконують в основному за величиною середньої теплоємності.

Для приблизних розрахунків при невисокій температурі значення середніх теплоємностей С_m газів приймають незалежно від температури згідно з даними таблиць 2 і 3 за величиною мольних середніх теплоємностей μС_m.

Таблиця 2

Гази	Мольна теплоємність μСm, кДж/кмоль·гр
	Ізохорна μСυ	Ізобарна μСр
Одноатомні (Аr, Не, Сl…)	12,56	20,93
Двохатомні (N2, О2, СО…)	20,93	29,31
Трьох- і багатоатомні (СО2, Н2О, SО2…)	29,31	37,68

Основні співвідношення між указаними теплоємностями та деякі залежності для визначення кількості теплоти наведені в таблиці 3.

Якщо розрахунки q виконуються через об’ємну середню теплоємність , то питома кількість теплоти q’ буде віднесена до 1м³ і має розмірність кДж/ м³.

В адіабатному процесі теплообмін відсутній і кількість теплоти у такому процесі рівна нулю, q_S =0. Таким чином, теплота є функція процесу.

Для m (кг) робочого тіла кількість теплоти розраховується згідно із залежністю

Q = m· q = mC_m(t₂ – t₁), кДж,

де q – питома кількість теплоти, віднесена до 1 кг РТ , кДж/кг.

Для об’єму V, м³, кількість теплоти визначається через її питому кількість q, віднесену до 1 м³ робочого тіла

, кДж.

Якщо об’єм РТ (V) виразити через його масу, то

, кДж,

де m = Vρ, кг; ρ – густина робочого тіла при відомих значеннях тиску Р і температури Т робочого тіла, кг/м³.

Якщо підставити секундні витрати робочого тіла m_c (кг/с), то будуть одержані секундні витрати теплоти, що мають розмірність кДж/с = кВт,

, кДж/с (кВт).

де q – питома кількість теплоти, необхідної для зміни температури 1кг робочого тіла від t₁ до t₂ при ізохорному q_υ, ізобарному q_р та політропному q_п процесах, у кДж/кг.

Теплота – це енергія, яку робоче тіло отримує або віддає в процесах теплообміну без здійснення роботи. При Q > 0 теплота отримується, t₂ > t₁, а якщо Q < 0 – то віддається і t₂ < t₁. При t₁ = t₂ кількість теплоти Q = 0.

При теплообміні між кількома РТ або РТ і навколишнім середовищем кількість теплоти, що віддається більш нагрітим тілом, Q₁ дорівнює кількості теплоти, яку отримує холодніше тіло, Q₂

Q₁ = Q₂; Q₁ – Q₂ = 0.

Таблиця 3

№ з/п	Вид теплоємності	Од. вимірювання	Ізохорна Сmυ	Ізобарна Сmр	ППолітропна Сmп	Об’ємна середня	Масова середня Сm
1	2	3	4	5	6	7	8
1	Мольна середня μСm		, k – показник адіабати		Сmр – Сmυ = R R – постійна газова стала		μСm=Сm·μ
2	Об’ємна середня = μСm/22,4						= Сm·ρ
3	Масова середня Сm= μСm/μ		μСmр – μСmυ = Rμ,			Сm= ·υ	–
4	ізохорна, υ= const, Сmυ		–		qυ = Сmυ· (t2–t1),
5	ізобарна, Р= const, Сmр		Сmр = Сmυ ·k	qр = Сmр· (t2–t1),
6	політропна, n= const, Сmп		Сmп=	qп = Сmп· (t2–t1),

Залежність називається рівнянням теплового балансу. Воно покладено в основу всіх розрахунків, повязаних із передачею теплоти від одного робочого тіла до другого.

К ількість теплоти, що виділяється при повному спалюванні палива, називається теплотою згорання палива . За відсутності конденсації водяної пари, що входить до складу продуктів згорання, теплота згорання 1нм³ природного газу становить 36000–37000 кДж/нм³. Величина теплоти згорання збільшується за наявності у складі палива важких вуглеводнів. Теплота згорання використовується при визначенні витрат палива B, нм³, згідно з формулою (11) за відомою величиною кількості теплоти Q, кДж, що витрачається для здійснення будь-якого термодинамічного процесу, нм³/год:

де – ККД перетворення теплоти згорання палива у теплоту робочого тіла, дол.од.

Робота є однією з форм передачі енергії при здійсненні термодинамічних процесів, у ході яких змінюється об’єм робочого тіла. При підведенні теплоти Q і розширенні РТ робота додатня, що ставиться за мету для більшості термодинамічних процесів. При зменшенні об’єму V і стискуванні РТ – робота від’ємна, що означає витрати зовнішньої роботи.

В еличина роботи, пропорціональна тиску Р, зміні об’єму РТ, обчислюється за формулою

l кДж/кг,

де l – робота в термодинамічному процесі зміни питомого об’єму робочого тіла від υ₁ до υ₂, м³/кг;

Р – тиск у процесі, кПа.

Для маси m, кг, робота визначається за формулою

кДж .

Для одержання максимальної роботи необхідно підвищувати тиск РТ і вибирати робочі тіла із значним питомим об’ємом (малою густиною). Формули, що застосовуються для визначення величини роботи, залежать від виду термо -

динамічного процесу і наведені у таблиці 5. Робота є функцією процесу.

Внутрішня енергія U, на відміну від роботи, залежить не від виду процесу, а є функцією термодинамічних параметрів, U= f (Р, υ, Т).

Для ідеального газу U= f (Т), оскільки сили міжмолекулярної взаємодії для ідеального газу відсутні.

Відповідно до сучасних фізичних поглядів внутрішня енергія є сумою кінетичної і потенціальної енергії молекул РТ. Температура Т визначає кінетичну енергію руху молекул, а від Р і υ залежить потенціальна енергія міжмолекулярної взаємодії.

Автор понять „внутрішня енергія” й „ентропія”, німецький фізик Р.Клаузис називав внутрішню енергію U „теплом, що міститься у робочому тілі”, проти поставляючи йому Q – „тепло, яке передається до робочого тіла”. Змінити внутрішню енергію робочого тіла можна при його взаємодії з іншими тілами або навколишнім середовищем. При цьому обмін масами РТ відсутній. Внутрішня енергія змінюється за рахунок підведення або відведення теплоти, здійснення над РТ роботи чи одночасно шляхом обміну і теплотою, і роботою. До сталого стану робочого тіла з певною внутрішньою енергією можна прийти, по-різному комбінуючи кількість теплоти і роботи, що передається до робочого тіла, залишаючи постійною лише їх суму.

Зміна внутрішньої енергії ΔU_п-к у термодинамічних процесах визначається як різниця внутрішніх енергій у кінцевій і початковій точках процесу

ΔU_к-п = U_к – U_п = С_mυ(Т_к – Т_п).

Величина внутрішньої енергії для ідеального газу з температурою t не- залежно від виду процесу обчислюється за формулою

U = С_mυ·t, кДж/кг,

де t – температура ідеального газу, °C; С_mυ – ізохорна середня масова теплоємність газу , кДж/кг·гр.

Поняття “ентальпія” було введене в термодинаміку Гіббсом як повна енергія робочого тіла, що складається із внутрішньої енергії U і потенціальної енергії рυ

і = U+ рυ = U + RT, кДж/кг.

Ентальпія має розмірність енергії і є функцією стану, оскільки залежить від параметрів стану робочого тіла (Р, υ, Т).

Для ідеальних газів силами міжмолекулярної взаємодії нехтують, тому ентальпія ідеального газу залежить тільки від температури і = f(Т) і визна-чається за залежністю

і = С_mр ·Т, кДж/кг,

де Т – температура робочого тіла за шкалою Кельвіна, ⁰К.

При виконанні практичних розрахунків із водяною парою температуру приймають за шкалою Цельсія й умовно вважають, що при температурі t = 0°C величина ентальпії РТ матиме нульове значення, і = 0. Це пояснюється переходом води у тверду фазу при t = 0 °C.

У теплотехнічних розрахунках, як правило, необхідно знати зміну ентальпії Δі = і_к – і_п, а не її абсолютне значення, а тому початок відліку (°К чи °C) для кінцевого результату (Δі) не має значення.

Для будь-якого термодинамічного процесу зміна ентальпії може бути записаною у диференціальній формі

dі = dU + d(рυ) = dU + рdυ + υdр.

Оскільки dq = dU + dl, а dl = рdυ, то

dі = dq + υdр,

а для ізобарного процесу, dр = 0

dі = dq,

Δі = q = і_к – і_п = С_mр(Т_к –Т_п),

де і_п, і_к – ентальпія відповідно у початковій та кінцевій точках ізобарного процесу, кДж/кг.

Ентропія була введена у термодинаміку теоретично, бо не існує інструментальних методів її вимірювання. Введення ентропії дало можливість установити зв’язок між температурою робочого тіла та кількістю теплоти і пояснити деякі фізичні явища. Наприклад, як пояснити, чому при фазових переходах реальних РТ підвищення теплоти не приводить до зміни температури тіла?

Якщо до ідеального робочого тіла спочатку підвести деяку кількість теп-

лоти Δq₁, а потім віддати деяку меншу кількість теплоти Δq₂ холодильнику, то в результаті буде виконана робота, на яку буде витрачена теплота Δq₀ = |Δq₁| – |Δq₂|. Теплота і температури нагрівача та холодильника для ідеального теплового двигуна зв’язані залежністю

Δq₁/Т₁ = Δq₂/Т₂, або Δq₁/Т₁– Δq₂/Т₂ = 0,

де знак «–»перед Δq₂ свідчить про те, що теплота віднімається від робочого тіла. Таким чином, у термодинамічних процесах ідеального теплового двигуна сталою є не кількість теплоти, одержаної Δq₁ чи втраченої Δq₂ РТ, а інша величина – теплота, що бере участь у процесі, поділена на температуру. При підведенні до РТ теплоти Δq ця величина змінюється на величину ΔS, що визначається як

ΔS = Δq/Т, кДж/кггр.

Величину „S” Клаузис назвав ентропією. Вона характеризує стан робочого тіла, як і Р, υ, Т.

Для будь-якого зворотного ідеального циклу зміна ентропії (інтеграл Клаузиса) буде рівним нулю

.

Із рівняння видно, що для зворотного термодинамічного процесу кількість теплоти, підведеної до РТ, визначається залежністю

Q = Т ·ΔS, кДж/кггр,

де ΔS – зміна ентропії, що може бути визначена за формулою

ΔS = С_mυ ln(Т_к/Т_п) +R ln(υ_к/υ_п), кДж/кггр

де індекси к і п означають відповідно початок та кінець процесу.

Реальні технічні процеси не є зворотними. Для повернення РТ у вихідний стан і повторного здійснення циклу необхідно витратити зовнішню роботу. І якщо теплота Δq₁ передається від гарячого джерела до робочого тіла при температурі Т₁ і не відновлюється, ентропія РТ або системи після такого процесу збільшується на величину Δq₁/Т₁.

Таким чином, у незворотних реальних технічних процесах ізольованої системи ентропія буде збільшуватись і зміна ентропії буде більшою за кількість теплоти, що підводиться до робочого тіла, поділену на абсолютну температуру тіла

ΔS > Δq/Т.

Енергія системи при цьому зменшується за рахунок її розсіювання. Працездатність системи падає на величину

Δl =Т₂ ΔS.

Таким чином, у всіх реальних незворотних процесах розширення робочого тіла, одержання роботи, передачі теплоти, тертя, дифузії тощо збільшується ентропія. Це плата за одержання роботи чи теплоти. Ентропія ізольованої системи збільшується до такого стану, коли ентропія досягне максимального значення, а сама система прийде в стан термодинамічної рівноваги, коли в ній припиняться всі незворотні процеси.

Якщо в початковій точці процесу прийняти нормальні умови (Т_п=273 °К, ρ_п= 101,3 кПа, υ_п=1/ρ_п , ρ_п = μ/22,4), то величину ентропії для будь-якого стану

робочого тіла з параметрами Р_к , υ_к , Т_к можна визначити за формулою

S_к =С_mυln(Т_к/273) +Rln(υ_к/υ_п) =С_mυln(Т_к/273) +Rln(Р_п/Р_к), кДж/кггр.