7.6.Вероятность попадания нормально распределенной случайной величины на заданный участок. Функция Лапласа.

Вычислим для случайной величины X, подчиненной нормальному закону, вероятность попадания на заданный участок (α,β).

Известно, что

Сделаем замену переменной

Получим

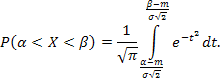
Известно, что интеграл не выражается через элементарные функции. Поэтому для его вычисления пользуются таблицами специальной функции, так называемой функций Лапласа или интеграла вероятностей

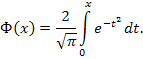
С помощью функции Лапласа может быть найдена вероятность попадания на участок:

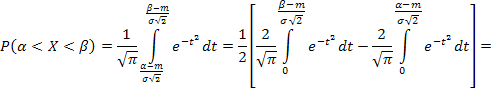
На практике часто пользуются другими формулами функции Лапласа, например, . Функция Ф₀(x) обычно называется нормированной функцией Лапласа. Найдем вероятность попадания нормально распределенной случайной величины на участок ( ), используя нормированную функцию Лапласа

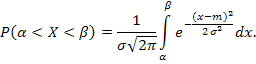
Сделаем следующую замену переменной

Функции Ф(х) и Ф₀(х)имеют следующую связь

Функция Лапласа имеет следующие свойства:

1. Ф₀(0) = 0

Это объясняется тем, что пределы интегрирования при х = 0 совпадают.

2. Ф(∞) = 1.

В самом деле,

3. Функция Лапласа есть нечетная функция своего аргумента, т.е.:

Ф(-х) = -Ф(х),

Ф₀(х) = -Ф₀(х).

В самом деле

Положим t = -U, получим

Таблицы функции Лапласа приводятся в книгах по теории вероятностей, математической статистике и многих справочных изданиях по математике.

Часто на практике решается задача определения вероятности попадания нормально распределенной случайной величины X, на участок длины 2l, симметричной относительно математического ожидания или центра рассеивания т.

Таким образом, формула для вероятности попадания нормально распределенной случайной величины X на участок, симметричней относительно математического ожидания, имеет вид

Аналогично можно показать, что

Если теперь положить l=kσ, то

Найдем значения этой вероятности для k = 1,2,3.

Этот результат означает, что примерно 68,3% всех значений нормально распределенной случайной величины лежит в интервале (m – σ, m + σ)

Более 95% всех значении нормально распределенной случайной величины лежит в интервале (m - 2σ, m+2σ).

Наконец,

Это значит, что практически все значения (99.7%) нормально распределенной случайном величины находятся в интервале трех сигм. Это важное свойство нормально распределенной случайной величины, называемое «правилом 3-х сигм», часто используется в практических приложениях теории вероятностей.

Выразим функцию распределения F(x) случайной величины X, подчиненной нормальному закону распределения, через функцию Лапласа.

Имеем

Если воспользоваться функцией Ф₀(х), то

7.7. Распределения, связанные с нормальным

В математической статистике широко используется для проверки гипотез и оценки неизвестных параметров распределения целый ряд статистических критериев, построенных на основе распределений . Для этих распределений имеются стандартные таблицы во многих учебниках и руководствах.

Нормированное нормальное распределение (z).

Если X нормально распределенная случайная величина с параметрами т и σ, то величина также распределена нормально с параметрами m_z = 0 и σ_z = 1. Плотность распределения и функция распределения величин Z имеют вид:

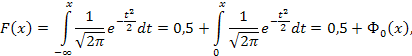
где x = Z – текущая переменная.

Рис. 6.10

Значения функций f(x) и Ф₀(х) табулированы. График плотности распределения величины Z представлен на рис. 6.10. Переход от произвольного нормального распределения X к нормированному z проводится лишь путем преобразования оси абсцисс в соответствии с выражением z = (x - m)/σ

Распределение К.Пирсона (χ²)

Если X_i(i=1,2,3,...,n) - нормально распределенные независимые случайные величины, причем математическое ожидание каждой из них M[Х_i] = 0, а среднее квадратичное отклонение σ[Х_i] = 1, то сумма квадратов этих величин распределена по закону χ² («хи» - квадрат) с f = n - r степенями свободы, где r -число связей, наложенных на величины X_i. Например, если величины X_i, связаны одним линейным соотношением , то число степеней свободы f = n – 1.

Плотность распределения величины χ² имеет вид:

где L(f) – функция, зависящая от числа степеней свободы f;

x = χ² – текущая переменная.

Распределение χ² определяется одним параметром - числом степеней свободы f. График плотности распределения закона χ² для различных чисел степеней свободы представлен на рис. 6.11. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

Математическое ожидание и дисперсия величины χ² равны M[χ] = f; D[χ²] = 2f.

Рис. 6.11

Распределение Стьюдента (t)

Если Z - нормально распределенная случайная величина, причем M[Z] = 0 и σ[Z] = 1, а независимая от z величина, которая распределена по закону χ² с f степенями свободы, то величина имеет распределение Стьюдента с f степенями свободы.

Рис. 6.12

Плотность распределения величины t имеет вид:

где B_f – функция зависящая от числа степеней свободы f;

x = i- текущая переменная.

Распределение t определяется одним параметром - числом степеней свободы f. График плотности распределения t для f = 3 представлен на рис. 6.12. С увеличением числа степеней свободы распределение быстро приближается к нормальному.

Распределение Фишера(F)

Если U и V - независимые случайные величины, распределенные по закону χ² со степенями свободы f₁ и f₂, то величина имеет распределение, называемое распределением Фишера со степенями свободы f₁ и f₂.

Плотность распределения величины F имеет вид:

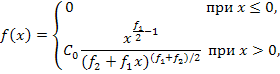
где C₀ - функция, зависящая от числа степеней свободы f₁ и f₂;

x = f – текущая переменная.

Распределение F определяется двумя параметрами - числами степеней свободы f₁ и f₂.

График плотности распределения F для чисел степеней свободы f₁ и f₂ представлен на рис.6.13.

Рис. 6.13