Лабораторна робота №5 Обчислення інтегралу „елементарним” методом Монте-Карло.

Пояснимо суть методу Монте-Карло на наступному прикладі. Уявимо прямокутник висотою та довжиною такий, що функція лежить всередині його (Рис.1).

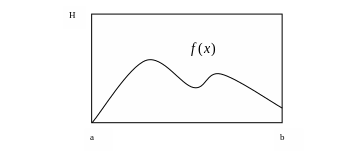
Згенеруємо пар випадкових чисел та , що задовольняють умовам та . Доля точок , що задовольняють умові представляють собою оцінку відношення інтегралу для функції на проміжку від до до площі прямокутника. Звідси випливає оцінка в методі спроб та помилок, що визначається співвідношенням

,

де - кількість точок, що папали під криву, - загальна кількість згенерованих пар точок.

Зазначимо, що точність обчислення інтегралу суттєво залежить від кількості згенерованих пар, а для оцінки точності обчислення інтегралу в загальному випадку необхідно проаналізувати залежність величини обчисленого значення інтегралу від кількості згенерований пар чисел. При цьому слід врахувати, що самі ці результати обчислень теж є випадковими величинами і при оцінках точності обчислення інтегралу потрібно користуватися статистичними методами щодо оцінок середнього значення цього інтегралу та середньо квадратичного відхилення кожного обчисленого значення інтегралу від середнього значення в межах кожної серії таких обчислень.

Для дослідження залежності точності обчислень від кількості згенерованих точок зазвичай проводять декілька серій із вимірів, (наприклад ) значень інтегралу для різної кількості згенерованих пар чисел ( 10,100,1000,10000 та 100000). Потім обчислюють середні значення інтегралу для цих серій обчислень та визначають середньо квадратичне відхилення отриманих результатів від відповідних середніх значень.

Завдання.

1. Обчисліть методом Монте-Карло значення інтегралу 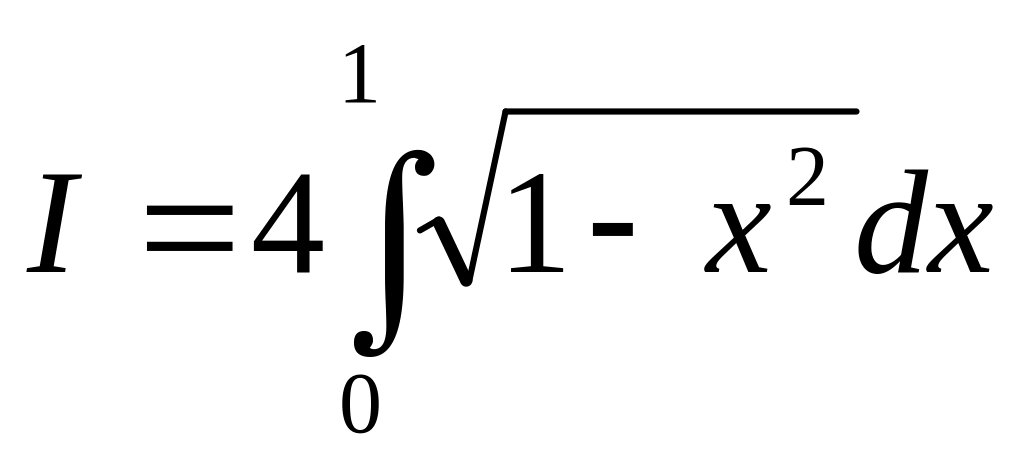для серій вимірів ( ) із відповідно N згенерованих пар чисел ( 10, 100, 1000, 10000, 100000). Порівняйте отриманий результат з добре відомим точним значенням цього інтегралу – числом .

2. Дослідіть середньо-квадратичні відхилення отриманих результатів обчислень від відповідних середніх значень інтегралу для серій з різною кількістю згенерованих пар чисел та визначте тенденції в залежності точності обчислень даного інтегралу для різних серій в залежності від кількості пар згенерованих в межах кожної серії чисел.

Порівняйте отримані результати обчислень середньо квадратичного відхилення з теоретично відомими з літератури, зокрема законом залежності середньо квадратичного відхилення для серій обчислень з різною кількістю згенерованих пар чисел .

3. Складіть письмовий звіт про виконання лабораторної роботи.

Звіт повинний містити в собі теоретичну частину, лістінг діючої програми розрахунку та висновки.

Контрольні запитання:

1. Дайте визначення математичному очікуванню.

2. Як працює генератор випадкових чисел.

3. Що означає термін рівномірного розподілу ймовірності.

4. Які реалізації методу Монте-Карло до підрахунку інтегралів крім того, що був описаний в даній лабораторній роботі, ви знаєте.