знайти область визначення функцій двох змінних:
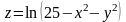
знайти приріст, частині похідні першого та другого порядків, змішані частинні похідні та повний диференціал функції та градієнт
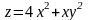в точці
.знайти рівняння дотичної площини та нормалі до поверхні в точці :
Знайти екстремум функції двох змінних, використовуючи необхідні умови екстремуму: у крузі .
знайти
екстремум функції на заданій лінії: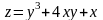 
,
якщо
.
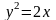Варіант
№10. 1. Розв’язати
систему за допомогою оберненої матриці: 
;
2. Розв’язати
систему лінійних рівнянь за методами
Крамера та Гауса: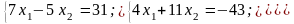 
3. Надаються координати вершин піраміди
А(2;2;2), В(0;5;2), С(0;2;8), D(2;5;10):
1.) записати вектори та знайти їх модулі;
2.) знайти кут між векторами ;
3.) знайти проекцію вектора на вектор ;
4.) знайти площу грані АВС та об’єм піраміди АВСD; 5.) скласти рівняння ребра АС та грані АВС.
4. Як розташовані фігури у просторі:
а.)
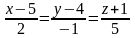i
;
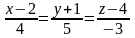б.) 2x-3y+4z-6=0 i x+2y-5z-=0.
5. Побудувати
криву другого порядку по її канонічному
рівнянню: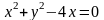 
.
6. Знайти границю функцій в точці:
а.)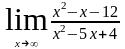
б.)
с.)
7. Знайти
похідну функцій за означенням:
.
8. Знайти
похідну: а.)
; б.)
.
9. Знайти
наближене значення за допомогою
диференціала відповідної функції
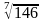замінивши х на 128.
10. Дослідити
та побудувати графік функції:
.
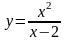знайти область визначення функцій двох змінних:
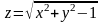
знайти приріст, частині похідні першого та другого порядків, змішані частинні похідні та повний диференціал функції та градієнт
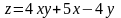в точці
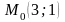.знайти рівняння дотичної площини та нормалі до поверхні в точці :
Знайти екстремум функції двох змінних, використовуючи необхідні умови екстремуму: у крузі .
знайти екстремум функції на заданій лінії:
,
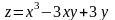якщо
.
Варіант
№11. 1. Розв’язати
систему за допомогою оберненої матриці: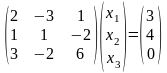 
;
2. Розв’язати
систему лінійних рівнянь за методами
Крамера та Гауса: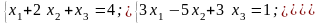 
3. Надаються координати вершин піраміди
А(1;3;2), В(-1;6;2), С(-1;3;8), D(1;6;10):
1.) записати вектори та знайти їх модулі;
2.) знайти кут між векторами ;
3.) знайти проекцію вектора на вектор ;
4.) знайти площу грані АВС та об’єм піраміди АВСD; 5.) скласти рівняння ребра АС та грані АВС.
4. Як розташовані фігури у просторі:
а.)
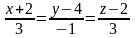i
;
б.) 2x-3y+4z-16=0 i 4x-y+4z-16=0.
5. Побудувати
криву другого порядку по її канонічному
рівнянню: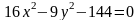 
.
6. Знайти границю функцій в точці:
а.)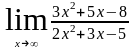
б.)
с.)
7. Знайти
похідну функцій за означенням:
.
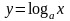8. Знайти похідну:
а.)
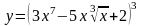; б.)
.
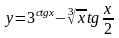9. Знайти
наближене значення за допомогою
диференціала відповідної функції
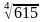замінивши х на 625.
10. Дослідити
та побудувати графік функції:
.
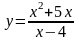знайти область визначення функцій двох змінних:
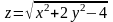
знайти приріст, частині похідні першого та другого порядків, змішані частинні похідні та повний диференціал функції та градієнт
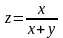в точці
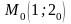.знайти рівняння дотичної площини та нормалі до поверхні в точці :
Знайти екстремум функції двох змінних, використовуючи необхідні умови екстремуму: в замкнутій області, обмеженій еліпсом .
знайти
екстремум функції на заданій лінії: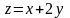 
,
якщо
.
Варіант
№12. 1. Розв’язати
систему за допомогою оберненої матриці: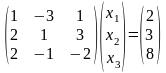 
;
2. Розв’язати
систему лінійних рівнянь за методами
Крамера та Гауса: 
3. Надаються координати вершин піраміди
А(0;1;2), В(-1;4;2), С(-2;1;8), D(0;4;10):
1.) записати вектори та знайти їх модулі;
2.) знайти кут між векторами ;
3.) знайти проекцію вектора на вектор ;
4.) знайти площу грані АВС та об’єм піраміди АВСD; 5.) скласти рівняння ребра АС та грані АВС.
4. Як розташовані фігури у просторі:
а.)
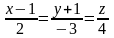i
;
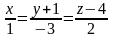б.) 2x-3y+5z=0 i 4x-6y+10z-13=0.
5. Побудувати
криву другого порядку по її канонічному
рівнянню: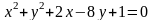 
.
6. Знайти границю функцій в точці:
а.)
б.)
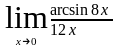с.)
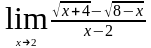
7. Знайти
похідну функцій за означенням:
.
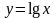8. Знайти похідну:
а.)
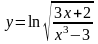; б.)
.
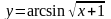9. Знайти
наближене значення за допомогою
диференціала відповідної функції
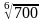замінивши х на 729.
10. Дослідити
та побудувати графік функції:
.
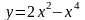