Министерство высшего и общего специального образования Самарский государственный аэрокосмический университет имени академика с.П. Королева

Кафедра ОКМ

Пояснительная записка к курсовой работе по курсу “Детали машин” Вариант №18-3

Выполнил студент группа 2305 Проверил преподаватель Курушин М. И.

Самара 20

Содержание

1 Кинематический и энергетический расчет дифференциального редуктора 3

2 Допускаемые напряжения зубьев зубчатых колес 5

3 Определение основных параметров планетарного редуктора в проектировочном расчете 8

4 Геометрический расчет параметров прямозубых цилиндрических зубчатых колес 11

5 Проверочный расчет прочности передачи 14

6 Геометрический расчет параметров прямозубых конических зубчатых колес 17

7 Проверочный расчет прочности конической передачи 22

8 Ориентировочный расчет валов 23

9 Проектировочный расчет валов 25

1 Кинематический и энергетический расчет дифференциального редуктора

Начальные условия:

P_вых=1900 кВт;

n_вх=n₁=11000 об/мин;

n_вых=n₃=n_П=1100 об/мин;

t_h=1100 ч.

Передаточное число редуктора

Принимаем отношение диаметров зубчатых колес сателлита k_r=1.75.

Передаточные числа ступеней в относительном движении (при остановленном водиле)

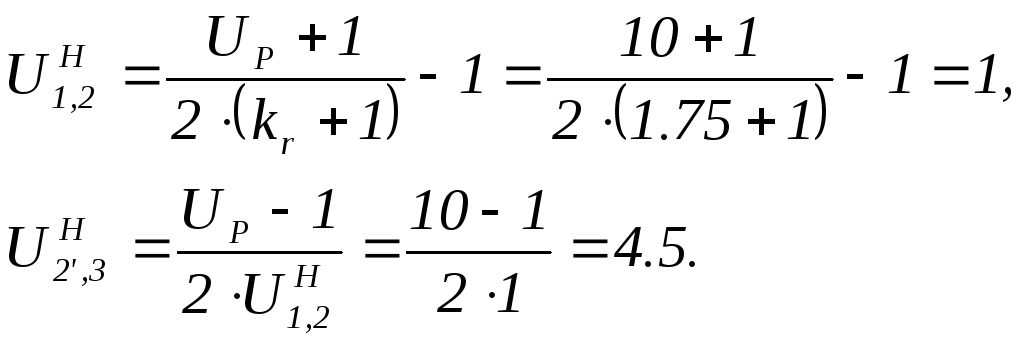
Обороты зубчатых колес в относительном движении (при остановленном водиле)

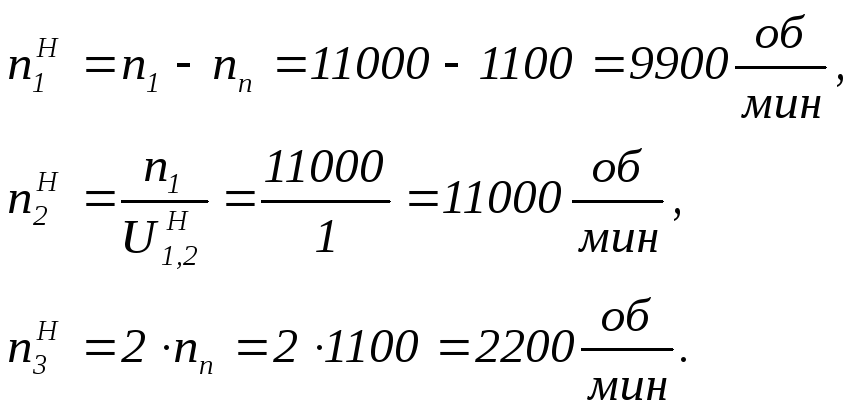
Принимаем шестую степень точности зубчатых колес.

КПД в зацеплениях при относительном движении

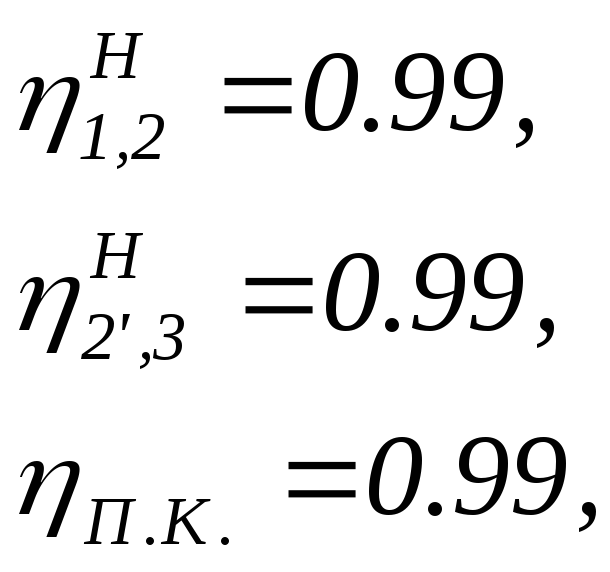
где _П.К.- КПД подшипников сателлитов.

КПД редуктора (суммарный)

Мощности на валах:

-мощность на входе в редуктор

-мощность на вале переднего винта

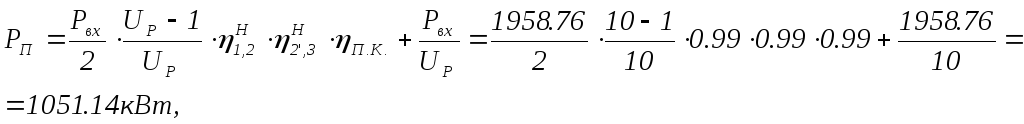
-мощность на вале заднего винта

Крутящий момент на входе (приводной вал)

Крутящий момент на выходе (валы винтов)

Зададим число зубьев солнечного колеса в запас из условия отсутствия подреза z_1o=17.

Расчетное число сателлитов (из условия соседства)

Принимаем целое число сателлитов из условия размещения перемычек водила между сателлитами а_с=5.

Коэффициент неравномерности распределения нагрузки по сателлитам k_нер=1.25- гибкое наружное колесо и «плавающее» солнечное колесо.

Расчетный крутящий момент в зацеплении на солнечном колесе

Крутящий момент на сателлите

2 Допускаемые напряжения зубьев зубчатых колес

2.1 Контактные напряжения

Исходные данные:

T1=TH, n1=nH, th1=0.55thП,

T2=0.87TH, n2=1.15nH, th2=0.25thП,

T3=0.83TH, n3=1.2nH, th3=0.20thП.

Выберем материал.

Принимаем цементируемую сталь 12Х2Н4А со свойствами:

• твердость на поверхности 56..63 НRС_Э,

• твердость сердцевины 35..40 НRС_Э.

Базовый предел контактной усталости

Hlim b=23HRCЭ,

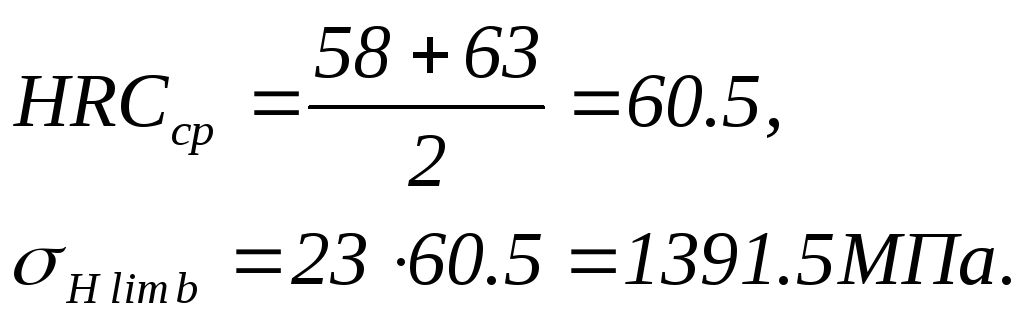
Базовое число цикла

NHO=12107.

Коэффициент эквивалентности по контактным напряжениям

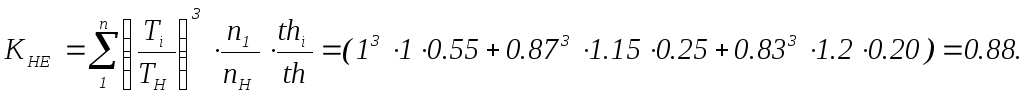
Эквивалентное число циклов перемены контактных напряжений

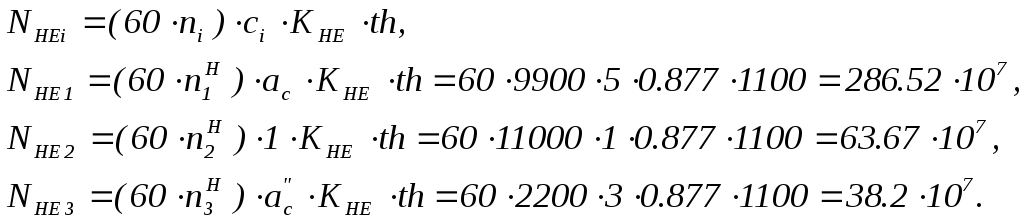
Коэффициент долговечности по контактным напряжениям

Если N_HE>N_HO , то K_Hl=1,

N_HЕ <N_HO , то по формуле 1K_Hl <1.8,

KHL1=1,

KHL2=1,

KHL3=1.

Запас контактной прочности

[SH]=1.2…1.35.

Принимаем [S_H]_ср=1.275.

Допускаемое контактное напряжение

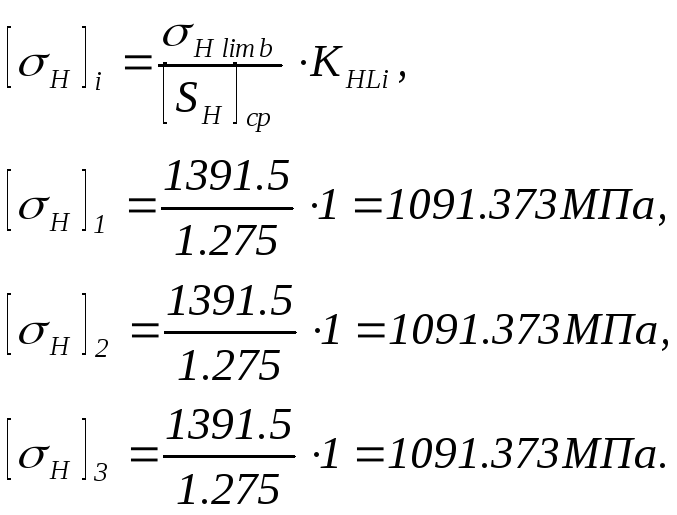
Принимаем

2.2 Изломные напряжения

Базовый предел изломной усталости

Flim b=750-850 Мпа.

Базовое число цикла

N_FO=410⁶.

Коэффициент эквивалентности по изломным напряжениям

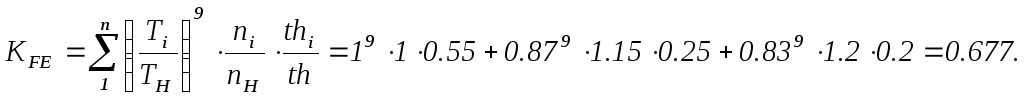
Эквивалентное число циклов перемены изгибных напряжений

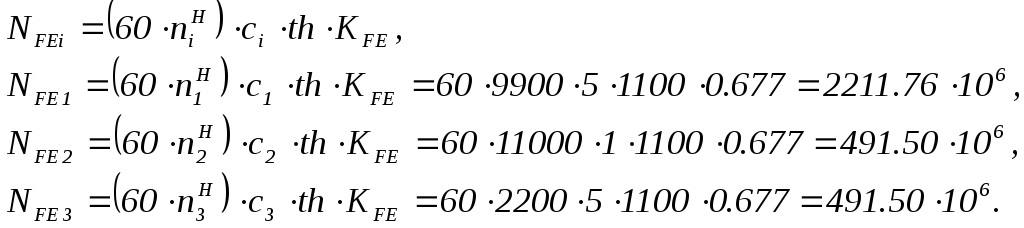
Коэффициент долговечности по изгибным напряжениям

При N_FE > N_FO принимают K_FL =1,

N_FЕ <N_FO , то по формуле 1K_FL <1.63,

Тогда:

K_FL1 =1,

K_FL2=1,

K_FL3=1.

Запас изломной прочности

[S_F]=1.7…2.0.

Принимаем [S_F]_ср=2.0.

Допускаемое напряжение изгиба

Для всех зубчатых колес для сателлитов
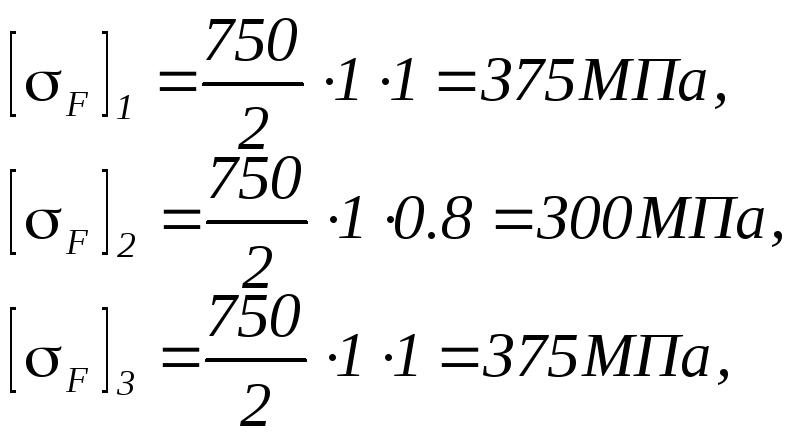