1.4. Уравнение Лагранжа
Дифференциальное уравнение движения механической системы в обобщенных координатах или уравнение Лагранжа имеет вид
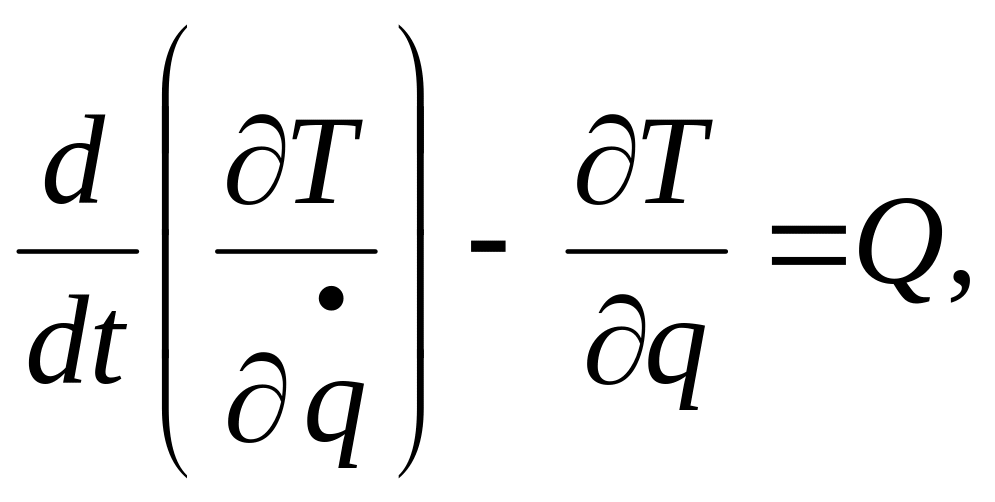(2)
где: Т – кинетическая энергия механической системы;
q – обобщенная координата;
- обобщенная скорость;
Q – обобщенная сила, соответствующая выбранной обобщенной координате.
В общем случае, для исследования механической системы с «n» степенью свободы необходимо составлять n уравнений Лагранжа.
Уравнения Лагранжа дают единый и при том достаточно простой метод решения задач динамики. Важное преимущество этих уравнений состоит в том, что их вид и число не зависят ни от количества тел (или точек), входящих в рассматриваемую систему, ни от того, как эти тела движутся; число уравнений Лагранжа определяется только числом степеней свободы системы. Кроме того, при идеальных связях в правые части уравнения (2) входят обобщенные заданные (активные) силы, и, следовательно, уравнения Лагранжа позволяют заранее исключить из рассмотрения все наперед неизвестные реакции связей.
Основная задача
динамики в обобщенных координатах
состоит в том, чтобы зная обобщенную
силу Q
и начальные условия, найти закон движения
системы в виде
,
т.е. определить обобщенную координату
как функцию времени. Так как кинетическая
энергия T
зависит от обобщенной скорости
,
то при дифференцировании первого члена
уравнения (2) по t
в левой части этого уравнения появляется
вторая производная по времени
от искомой координаты. Следовательно,
уравнение Лагранжа представляет собой
обыкновенное дифференциальное уравнение
второго порядка относительно обобщенной
координаты q.
Случай потенциальных сил. Если все действующие на механическую систему силы потенциальные, то уравнение (2) можно представить в виде:
(3)
или
(4)
Введем функцию
(5)
Функция L от обобщенных координат и обобщенных скоростей, равная разности между кинетической и потенциальной энергиями системы, называется функцией Лагранжа или кинетическим потенциалом. Тогда, в случае потенциальных сил уравнение (4) с учетом (5):
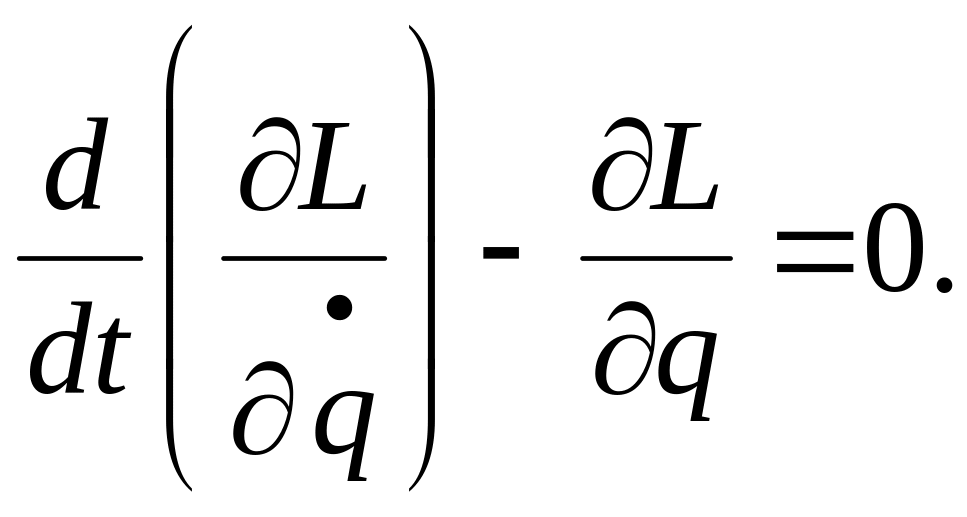(6)
Уравнение (6) справедливо потому, что потенциальная энергия П зависит только от обобщенной координаты q, а от обобщенной скорости не зависит.
Из полученного результата (6) следует, что состояние механической системы, на которую действуют потенциальные силы, определяется заданием одной только функции Лагранжа, так как, зная эту функцию, можно составить дифференциальные уравнения движения механической системы.
2. Методика решения задач
Уравнениями Лагранжа можно пользоваться для изучения движения любой механической системы с геометрическими* связями, независимо от того, сколько тел входит в систему, как движутся эти тела и какое движение (абсолютное или относительное) рассматривается.
Чтобы для данной механической системы составить уравнения Лагранжа, надо:
1) установить число степеней свободы системы и выбрать обобщенные координаты (для механической системы с одной степенью свободы выбрать одну обобщенную координату);
2) изобразить систему в произвольном положении и показать на рисунке все заданные силы (если связи неидеальные, то необходимо учесть и силы трения);
3
* геометрические связи – связи, налагающие
ограничения на положения точек системы
в пространстве, но не на их скорости
4) вычислить кинетическую энергию системы в ее абсолютном движении и выразить эту энергию через обобщенную скорость ;
5) подсчитать соответствующие частные производные от T по q и и подставить все вычисленные параметры в уравнение Лагранжа.
Из полученных уравнений, если заданы действующие силы и начальные действия, можно, интегрируя эти уравнения, найти закон движения системы в виде . Если же задан закон движения, то составленные уравнения позволяют определить заданные силы.
Когда все приложенные к системе силы потенциальные, уравнение Лагранжа можно составлять в виде (3) или (6). При этом, вместо вычисления обобщенной силы надо определить потенциальную энергию системы, выразив ее через обобщенную координату, и затем, взяв производную от П по обобщенной координате, подставить в уравнение (3). При необходимости можно составить функцию Лагранжа и воспользоваться уравнением (6).