
- •Вінницький фінансово-економічний університет
- •Імітаційне моделювання конспект лекцій
- •Тема 1 Вступ до курсу "Імітаційне моделювання"
- •1. Історія виникнення та розвиток імітаційного моделювання
- •2. Види моделювання та особливості їх використання
- •3. Основні напрями використання машинної імітації
- •4. Сфери застосування імітаційних моделей
- •5. Програмна реалізація імітаційних моделей
- •6. Приклад імітаційної моделі
- •III. Gpss — програма імітаційної моделі еом
- •Питання для самоконтролю
- •Тема 2 Сутність, розвиток і застосування імітаційного моделювання
- •1. Сутність та поняття імітаційного моделювання
- •2. Загальна схема і цілі імітаційного моделювання
- •3. Переваги і недоліки методу машинної імітації
- •4. Поняття імітаційного моделювання у вузькому та широкому сенсі
- •5. Імітація еволюційних процесів
- •Питання для самоконтролю
- •Тема 3 Основні етапи побудови імітаційних моделей
- •1. Види робіт при розробці імітаційної моделі.
- •2. Основні етапи побудови імітаційних моделей. Визначення задачі та її аналіз як етап побудови імітаційних моделей
- •3. Визначення вимог до інформації як етап побудови імітаційних моделей
- •4. Збирання інформації як етап побудови імітаційних моделей
- •5. Висунення гіпотез і прийняття припущень як етап побудови імітаційних моделей. Встановлення основного змісту моделі
- •6. Визначення параметрів, змінних і критеріїв ефективності як етап побудови імітаційних моделей. Описання концептуальної моделі і перевірка її вірогідності
- •7. Створення логічної структурної схеми як заключний етап побудови імітаційної моделі
- •Питання для самоконтролю
- •Тема 4 Імітаційна модель керування запасами
- •1. Поняття та сутність оптимального керування запасами
- •2. Основні параметри моделювання задачі керування запасами
- •3. Сутність та характеристика детермінованих моделей керування запасами
- •4. Керування багатопродуктовими запасами
- •5. Концептуальна імітаційна модель керування запасами
- •6. Блок-схема імітаційної моделі керування запасами
- •7. Аналіз результатів машинної реалізації імітаційної моделі
- •Питання для самоконтролю
- •Тема 5 Поняття про Метод Монте-Карло
- •1. Метод Монте-Карло в імітаційному моделюванні
- •2. Приклад застосування методу Монте-Карло
- •3. Точність оцінки ймовірності за допомогою відносної частоти.
- •4. Рівномірна випадкова послідовність чисел рвп [0,1]
- •5. Властивості рівномірної випадковості послідовності чисел
- •Питання для самоконтролю
- •Тема 6.Генерування рвп [0,1]
- •1. Поняття про генератори (датчики) випадкових чисел.
- •2. Табличний спосіб одержання рвп [0,1]
- •3. Фізичний спосіб одержання рвп [0,1]
- •4. Програмні способи одержання рвп [0,1]
- •5. Загально статистичні методи перевірки якості псевдовипадкових чисел
- •Питання для самоконтролю
- •Тема 7 Генерування випадкових подій і випадкових величин під час машинної імітації
- •1. Імітація випадкових подій
- •2. Стандартний метод імітації дискретно розподілених випадкових величин
- •3. Спеціальні методи імітації деяких дискретних розподілів
- •Питання для самоконтролю
- •Тема 8. Генерування неперервних випадкових величин
- •1. Суть проблеми імітації неперервних розподілів
- •2. Стандартний метод імітації неперервних випадкових величин
- •3. Метод добору (відбракування) неперервних випадкових величин
- •4. Наближене формування розподілів неперервних випадкових величин
- •5. Генерування нормально розподілених випадкових величин
- •Питання для самоконтролю
- •Тема 9 Планування імітаційних експериментів
- •1. Загальна характеристика планування імітаційних експериментів
- •2. Апроксимуючий поліном функції відгуку
- •3. Дворівнева система вимірювання факторів
- •4. Повні факторні плани та їхні властивості
- •5. Дробові факторні плани і умови доцільності їх застосування
- •6. Засоби планування експерименту системи statgraphics Планування експерименту (Experimental Design)
- •Питання для самоконтролю
- •Тема 10 Одержання апроксимуючих поліномів
- •2. Апроксимуючий поліном другого плану
- •1. Одержання коефіцієнтів лінійної регресії
- •2. Апроксимуючий поліном другого плану
- •3. Побудова композиційних планів
- •4. Ортогональний центральний композиційний експеримент
- •5. Рототабельний композиційний експеримент
- •Питання до самоконтролю:
- •Тема 11 Узагальнення та статистична перевірка результатів імітаційних експериментів
- •1. Перевірка результатів імітаційних експериментів за допомогою властивості однорідності дисперсій
- •2. Перевірка значущості коефіцієнтів регресії
- •3. Перевірка адекватності моделі
- •Питання для самоконтролю
- •Тема 12 Планування імітаційних експериментів у процесі дослідження та оптимізації систем
- •1. Планування імітаційних експериментів у процесі дослідження систем
- •2. Планування імітаційних експериментів у процесі оптимізації систем
- •Питання для самоконтролю
- •Список рекомендованої літератури
- •Навчальне видання:
5. Загально статистичні методи перевірки якості псевдовипадкових чисел
Зазвичай генерування псевдовипадкової послідовності передбачає два етапи. На першому генерують псевдовипадкові числа, що мають рівномірний розподіл на відрізку від нуля до одиниці. На другому цю послідовність перетворюють у послідовність, що має заданий закон розподілу.
Псевдовипадкові послідовності (числа) — послідовності, що отримуються за цілком невипадковим алгоритмом, але мають властивості, дуже подібні до властивостей реалізацій випадкових чисел.
Псевдовипадкове число — елемент отриманої за певним алгоритмом числової послідовності, властивості якої наближаються до випадкової. Негативною особливістю псевдовипадкових чисел (як імітаційної моделі випадкових чисел) є періодичність отриманої послідовності.
Для генерування псевдовипадкових чисел, що мають рівномірний розподіл на відрізку від нуля до одиниці використовують методи:
метод лишків (лінійний конгруентний метод);
метод середніх квадратів (метод фон Неймана);
метод трикутного відображення;
метод логістичного відображення.
Для перетворення отриманної послідовності у послідовність псевдовипадкових чисел із заданим законом розподілу використовують загальні та спеціальні методи. Серед загальних можна зазначити методи, що базуються на аналітичному перетворенні елементів вихідної послідовності; метод остач та метод, що базується на заміні заданого закону розподілу східчастою функцією. Ці методи придатні для отримання послідовностей з різними типами законів розподілу. До спеціальних належать алгоритми, що дають змогу переворити вихідну послідовність у послідовність з конкретним законом розподілу. Кожний з таких алгоритмів придатний лише для отримання псевдовипадкових послідовностей із заданим типом розподілу.
Обов'язковим етапом генерування псевдовипадкових чисел є перевірка періодичності й випадковості отриманої послідовності та її відповідності заданому закону розподілу.
Питання для самоконтролю
1. Які Ви знаєте способи генерування випадкових подій?
2. В чому полягає табличний метод генерування випадкових подій?
3. Які є переваги та недоліки при генеруванні випадкових подій табличним методом?
4. Якими пристроями користувались при фізичному генеруванні випадкових величин?
5. За допомогою яких фізичних явищ можна дістати реалізацію випадкових подій?
6. Що таке «песвдовипадкове число»?
7. Який є недолік методу серединних квадратів?
Тема 7 Генерування випадкових подій і випадкових величин під час машинної імітації
План
1. Імітація випадкових подій.
2. Стандартний метод імітації дискретно розподілених випадкових величин.
3. Спеціальні методи імітації деяких дискретних розподілів.
Література: [4, 5].
1. Імітація випадкових подій
У
загальному випадку під час імітаційного
моделювання часто виникає потреба
імітувати випадкові події, які можуть
мати різне призначення. Випадкові події
імітуються згідно зі схемою випробувань
за «жеребкуванням», сутність якої
полягає у такому. Нехай у результаті
спроби може настати одна з n несумісних
у сукупності подій
 що утворюють повну групу, причому
що утворюють повну групу, причому
 де
де
 — ймовірність появи події
— ймовірність появи події .
Якщо є генератор випадкових чисел
РВП
[0, 1] (рівномірна випадкова послідовність
чисел на відрізку), то схему випробувань
за «жеребкуванням» можна подати так.
.
Якщо є генератор випадкових чисел
РВП
[0, 1] (рівномірна випадкова послідовність
чисел на відрізку), то схему випробувань
за «жеребкуванням» можна подати так.
1)
Розбиваємо відрізок [0, 1] на n частин
завдовжки
 Координати точок поділу відрізка
Координати точок поділу відрізка
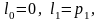

2)
Обираємо
 — наступне число із РВП [0, 1]. У разі, коли
— наступне число із РВП [0, 1]. У разі, коли
 ,
вважаємо, що відбулася подія
,
вважаємо, що відбулася подія .
Справді, за такої схеми
.
Справді, за такої схеми
 (7.1)
(7.1)
