
- •Ряды с неотрицательными членами.
- •Признак сравнения рядов с неотрицательными членами.
- •Признак Даламбера.
- •Признак Коши (радикальный признак).
- •Интегральный признак Коши.
- •Знакочередующиеся и знакопеременные ряды.
- •Признаки Даламбера и Коши для знакопеременных рядов.
- •Степенные ряды.
- •Функциональные ряды.
- •Степенные ряды.
- •Теоремы Абеля.
- •Действия со степенными рядами.
- •1) Интегрирование степенных рядов.
- •2) Дифференцирование степенных рядов.
- •3) Сложение, вычитание, умножение и деление степенных рядов.
- •Разложение функций в степенные ряды.
- •Применить формулу Маклорена:
- •Если применить к той же функции формулу Маклорена
- •Некоторые приложения степенных рядов Приближенное вычисление значений функций
- •Приближенное вычисление определеного интеграла
- •Решение дифференциальных уравнений с помощью степенных рядов.
- •Ряды Фурье.
- •Периодические функции. Периодические процессы.
- •Тригонометрический ряд.
- •Достаточные признаки разложимости в ряд Фурье.
- •Ряд Фурье для четных и нечетных функций.
- •Ряды Фурье для функций любого периода.
- •Разложение в ряд Фурье непериодической функции.
- •Ряд Фурье по ортогональной системе функций.
- •Интеграл Фурье.
- •Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу
Теоремы Абеля.
(Нильс Хенрик Абель (1802 – 1829) – норвежский математик)
Теорема.
Если степенной
ряд
сходится при x
= x10
, то он сходится и притом абсолютно для
всех
![]() .
.
Доказательство.
По условию теоремы, так как члены ряда
ограничены, то
![]() где k-
некоторое постоянное число. Справедливо
следующее неравенство:
где k-
некоторое постоянное число. Справедливо
следующее неравенство:
![]()
Из этого неравенства
видно, что при x<x1
численные величины членов нашего ряда
будут меньше ( во всяком случае не больше
) соответствующих членов ряда правой
части записанного выше неравенства,
которые образуют геометрическую
прогрессию. Знаменатель этой прогрессии
![]() по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.
по условию теоремы меньше единицы,
следовательно, эта прогрессия представляет
собой сходящийся ряд.
Поэтому на основании
признака сравнения делаем вывод, что
ряд
![]() сходится, а значит ряд
сходится, а значит ряд
![]() сходится абсолютно.
сходится абсолютно.
Таким образом,
если степенной ряд
сходится
в точке х1,
то он абсолютно сходится в любой точке
интервала длины 2![]() с центром в точке х
= 0.
с центром в точке х
= 0.
Следствие.
Если при х =
х1
ряд расходится, то он расходится для
всех
![]() .
.
Таким образом, для
каждого степенного ряда существует
такое положительное число R,
что при всех х
таких, что
![]() ряд абсолютно сходится, а при всех
ряд абсолютно сходится, а при всех
![]() ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
ряд
расходится. При этом число R
называется радиусом
сходимости.
Интервал (-R,
R)
называется интервалом
сходимости.
Отметим, что этот интервал может быть как замкнутым с одной или двух сторон, так и не замкнутым.

Радиус сходимости может быть найден по формуле:
По признаку
Даламбера:
![]() .
.
По признаку Коши:

Замечания:
Если
 ,
то можно убедиться, что степенной ряд
абсолютно сходится на всей числовой
оси. В этом случае
,
то можно убедиться, что степенной ряд
абсолютно сходится на всей числовой
оси. В этом случае
 .
Если
.
Если
 ,
то
,
то
 .
.Если степенной ряд сходится для положительного значения х=х1 , то он сходится равномерно в любом промежутке внутри
 .
.Интервал сходимости степенного ряда находится из неравенства
 ;
имеет вид
;
имеет вид
 .
.Если степенной ряд содержит не все степени х, т.е. задан неполный степенной ряд, то интервал сходимости ряда находят без определения радиуса сходимости, а непосредствено применяя признак Даламбера или Коши для ряда, составленного из модулей членов данного ряда.
Пример.
Найти область сходимости ряда
![]()
Находим
радиус сходимости
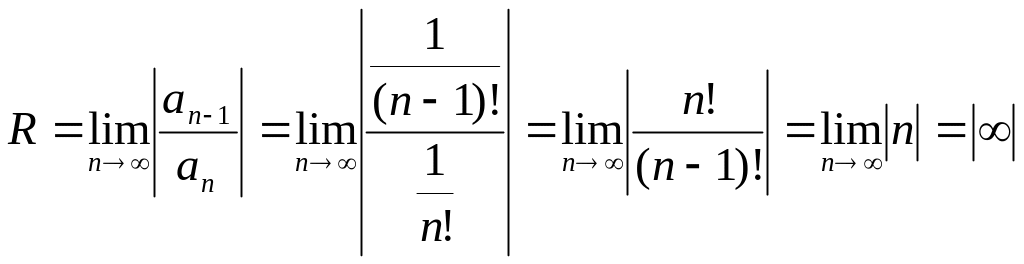 .
.
Следовательно,
данный ряд сходится при любом значении
х.
Общий член этого ряда стремится к нулю.
![]()
Пример.
Найти область сходимости ряда
![]()
![]() ,
,
![]() .
.
Ряд
абсолютно сходится, если
![]() . Исследуем поведение ряда на концах
интервала сходимости.
. Исследуем поведение ряда на концах
интервала сходимости.
При
х=-1 имеем ряд
![]() ,
который сходится по признаку Лейбница.
,
который сходится по признаку Лейбница.
При
х=1 имеем ряд
![]() ,
который тоже сходится.
,
который тоже сходится.
Следовательно, областью сходимости исходного ряда является отрезок [-1;1].
Пример.
Найти область сходимости ряда
![]() .
.
![]() ,
,
![]()
![]() .
.
При
х=-4 имеем ряд
![]() сходится по признаку Лейбница.
сходится по признаку Лейбница.
При
х=0 имеем расходящийся ряд
![]() .
.
Следовательно, областью сходимости исходного ряда является полуотрезок [-4;0).
Действия со степенными рядами.
1) Интегрирование степенных рядов.
Если
некоторая функция f(x)
определяется степенным рядом:
![]() ,
то интеграл от этой функции можно
записать в виде ряда:
,
то интеграл от этой функции можно
записать в виде ряда:
![]()
