Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу
Тогда
- двойной
интеграл Фурье.
Окончательно
получаем:
представление функции f(x) интегралом Фурье.
Замечания:
Если функция f(x) – четная, то формула Фурье принимает вид
;
Если функция f(x)
– нечетная, то формула Фурье принимает
вид
.
Если функция f(x) задана лишь на промежутке
,
то ее можно продолжить на промежуток
разными способами, в частности – четным
и нечетным образом.Формулу Фурье можно представить в симметричной форме записи, если положить, что
.
В случае четной функции:
;
в случае нечетной функции:
.
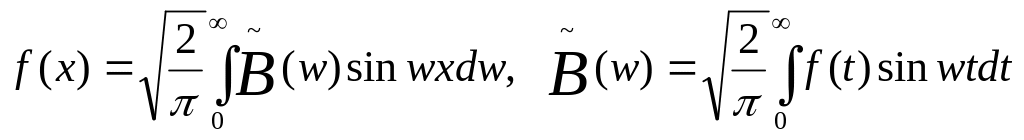Функции
называются соответсвенно
косинус-преобразованием
и синус-преобразованием
Фурье для
функции f(x).
Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:
Определение.
Если f(x)
– любая абсолютно интегрируемая на
всей числовой оси функция, непрерывная
или имеющая конечное число точек разрыва
первого рода на каждом отрезке, то
функция
называется преобразованием Фурье функции f(x).
Функция F(u) называется также спектральной характеристикой функции f(x).
Если f(x) – функция, представимая интегралом Фурье, то можно записать:
Это равенство называется обратным преобразованием Фурье
Пример.
Представить
интегралом Фурье функцию
.
Функция
удовлетворяет условиям представимости
интегралом Фурье, абсолютно интегрируемая
на промежутке
:
.
Функция нечетная, принимает формулу:
.
Следовательно,
.