1.6. Результаты решения транспортной задачи.

Пункт добычи	Клиент	Количество перевозок, тыс.т.	Расстояние перевозок, км.	Грузооборот, млн.ткм.	Стоимость перевозок, у.е.
1	1	30	5200	156	126
	2	17	6800	115,6	90,1
2	2	9	3900	35,1	23,4
	4	39	3900	152,1	148,2
3	3	53	5800	307,4	190,8
	4	7	4000	28	31,5
итого					610,0

2. Рапределительная задача.

2.1. Исходные данные для распределительной задачи.

Для работы с клиентами порт располагает флотом трёх типов Ф₁, Ф₂, Ф₃ в количестве

;

;

;

.

Имеются матрицы эксплуатационных расходов по одному за расчётный период Э и провозной способности различных типов флота по участкам работы :

11,2 12,1 10,6 10,9 9,9 9,6

Э= 8,8 8,0 9,0 9,9 10,0 9,0 у.е.

7,4 8,3 8,2 7,8 7,8 9,0

14,2 11,6 12,1 13,7 11,0 9,8

П= 19,3 7,8 10,0 11,5 13,1 10,8 млн.ткм.

13,6 10,0 8,5 7,9 14,0 9,9

2.2. Эмм распределительной задачи.

1. Критерий эффективности – минимальные эксплуатационные расходы

2. Целевая функция:

,

где Х_ij – количество i-го типа флота, работающего на j-м участке.

Система ограничений:

По флоту:

По грузообороту:

Дополнительные условия: - количество i-го типа флота, работающего на j-м участке.

2.3. Метод эквивалентов.

Алгоритм:

1. Выбираем базисный тип флота, для которого на всех или большинстве участков работы наименьшая провозная способность, ему присваивается эквивалент .

2. Рассчитываются эквиваленты всех других типов флота на каждом участке работы по формуле - эквивалент i-го типа флота, работающего на j-м участке.

3. К матрице достраиваются дополнительные столбцы и строки. В каждом дополнительном столбце находится разница между двумя максимальными эквивалентами, по каждой строке, в каждой дополнительной строчке – между двумя максимальными эквивалентами по столбику.

4. Из значений в каждой дополнительной строке и столбце выбирается максимальное и рассматривается соответствующая строка или столбец.

5. Выбирается клетка с максимальным эквивалентом и загружается первой

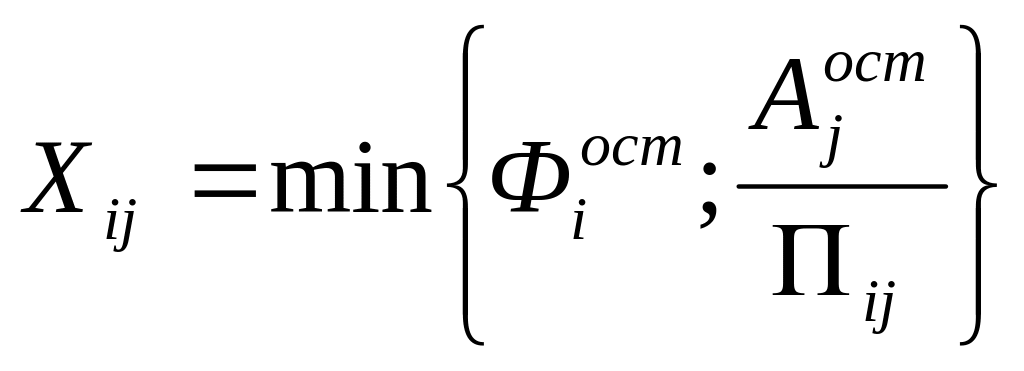
6. Из рассмотрения исключается столбец и строка, где ресурсы исчерпаны.

7. Алгоритм повторяется до исчерпания всех ресурсов.

	156	115,6	35,1	152,1	307,4	28
24	14,2 104 11,2	9,96 11,6 116 12,1	2,9 12,1 142 10,6	11,1 13,7 173 10,9	11,0 79 9,9	0,04 9,8 99 9,6	31	31	26	17	20
19	8,08 19,3 142 8,8	7,8 78 8,0	10,0 118 9,0	11,5 146 9,9	13,1 94 10,0	2,55 10,8 109 9,0	4	28	9	15	15	15	94
28	13,6 100 7,4	10,0 100 8,3	8,5 100 8,2	7,9 100 7,8	21,95 14,0 100 7,8	9,9 100 9,0	0	0	0	0	0	0	100
	38	16	24	27	6	9	1
		16	24	27	6	9	2
		16	24		6	9	3
		16			6	9	4
					6	9	5
					6	9	6
					6		7

Все полученные Х_j подставляются в систему ограничений, тем самым вариант решений проверяется на допустимость. Все выражения системы ограничений должны оказаться верными. Далее рассчитывается значение целевой функции.

Проверка ограничений:

По флоту:

По грузообороту:

Целевая функция:

у.е.