Министерство транспорта и связи

Служба речного флота

Новосибирская государственная академия водного транспорта

Кафедра: УРФ

Дисциплина: Методы моделирования и оптимизации транспортных процессов

Курсовая работа

на тему:

«Выбор оптимальной схемы доставки грузов»

Выполнил:

Проверил:

Содержание

Введение…………………………………………………………………………………………3

1. Транспортная задача………………………………………………………………………….4

1.1. Исходные данные для транспортной задачи……………………………………...4

1.2. ЭММ транспортной задачи………………………………………………………...4

1.3. Метод Фогеля………………………………………………………………………..5

1.4. Метод минимального элемента в матрице………………………………………..6

1.5. Методом потенциалов.……………………………………………………………..7

1.6. Результаты решения транспортной задачи….…………………………………….9

2. Распределительная задача…………………………………………………………………...10

2.1. Исходные данные для распределительной задачи………………………….……10

2.2. ЭММ распределительной задачи…………………………………………….…....10

2.3. Метод эквивалентов………………………………………………………………..11

2.4. Метод анализа разности себестоимости………………………………………….13

2.6. Результат решения распределительной задачи………………………….……….19

Заключение……………………………………………………………………….……………..20

Список используемой литературы…………………………………………………….………21

Введение

Имеется три пункта добычи ПГС: i = 1, 2, 3 с объёмами добычи Q = (а₁, а₂, а₃) тыс. тонн. Требуется составить план перевозок добываемой ПГС четырём клиентам: j = 1, 2, 3, 4 c объемами спроса = (b₁, b₂, b_3, b₄) тыс. тонн так, чтобы сформировать участки грузовой работы, отвечающие минимальной общей стоимости доставки.

При этом матрица удельной стоимости доставки С:

;

Матрица расстояний между пунктами L:

.

Затем по сформированным участкам грузовых работ расставить наличное количество флота трёх типов, так, чтобы эксплутационные расходы при этом оказались наименьшими.

Имеются матрицы эксплутационных расходов по одному судну за расчётный период Э и провозной способности различных типов флота по участкам работ П.

1. Транспортная задача.

1.1. Исходные данные для транспортной задачи.

Имеется три пункта добычи ПГС: i=1, 2, 3 с объёмами добычи Q=(47,48,60) тыс. тонн. Требуется составить план перевозок ПГС четырём клиентам: j=1, 2, 3, 4 c объемами спроса Q=(30,26,53,46) тыс. тонн так, чтобы сформировать участки грузовой работы, отвечающие минимальной общей стоимости доставки.

При этом матрица удельной стоимости доставки С:

;

Матрица расстояний между пунктами L:

.

1.2. Эмм транспортной задачи.

1. За критерий эффективности принимаем минимальную общую стоимость доставки.

2. Целевая функция:

;

3. Ограничения:

4. Дополнительные условия: 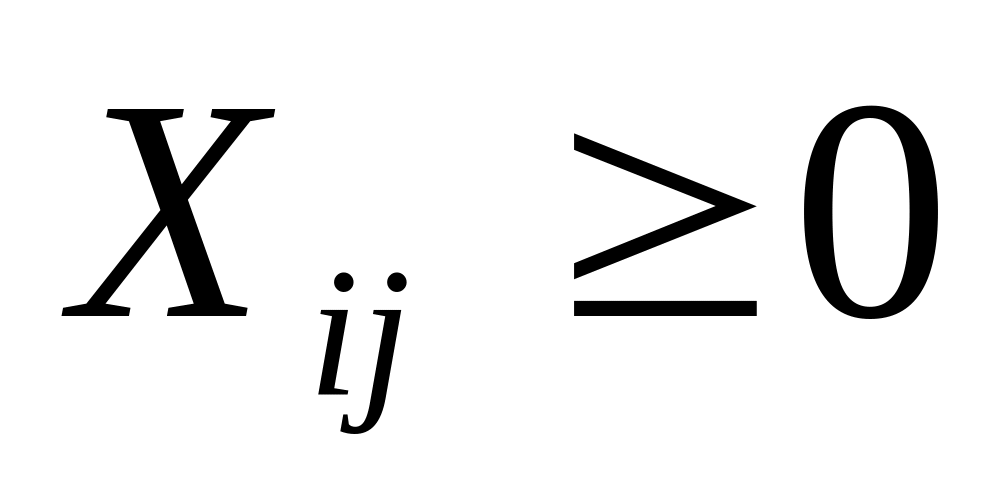- количество груза, перевозимого от i-го пункта добычи j-му потребителю.

1.3. Метод Фогеля.

Алгоритм:

1. Формируется матрица из величин а_i, в_j, с_ij.

2. Анализируется значение оценочных величин в каждой строке и каждом столбце.

3. Находится разница между двумя минимальными значениями, если и двумя максимальными, если этих величин по каждой строке и каждому столбцу. Заносится в дополнительный столбец и дополнительную строку.

4. Из всех разностей в дополнительной строке и столбце находится максимальная и рассматривается строка и столбец к которым она принадлежит.

5. В них находится минимальное значение оценочной величины, если и максимальное, если .

6. Клетка соответствующая этому значению загружается первой из условия .

7. Из рассмотрения исключается столбец или строка, где ресурсы исчерпаны.

8. Алгоритм повторяется без учёта исключённых столбцов и строк до исчерпания всех ресурсов.

9. Проверяются ограничения задачи и вычисляются значения целевой функции.

Вj ai	30		26		53		46
47	30						17		1,1	1,9	0,9	7,0
		4,2		5,3		6,1		7,0
48			26				22		0,3	0,9	1,6	3,8	3,8	3,8
		2,9		2,6		5,4		3,8
60					53		7		0,9	0,9	0,9	4,5	4,5
		6,2		5,0		3,6		4,5
	1,3		2,4		1,8		0,7
	1,3				1,8		0,7
					1,8		0,7
							0,7
							0,7
							3,8

Клетка Х₂₂=min(48;26)=26

Х₁₁=min(47;30)=30

Х₃₃=min(60;53)=53

Х₁₄=min(47-30;46)=17

Х₃₄=min(60-53;46-17)=7

Х₂₄=min(48-26;46-17-7)=22

Проверим план на невырожденность Z=m+n-1,

где Z- количество базисных клеток;

m,n- количество строк и столбцов матрицы;

Z=3+4-1=6 -- план не вырожден

Проверим план на допустимость: подставим все Х_ij в системы ограничений

По поставщикам

30+0+0+17=47

0+26+0+22=48

0+0+53+7=60

По потребителям

30+0+0=30

0+26+0=26

0+0+53=53

17+22+7=46

Ограничения выполняются, значит план является допустимым.

Рассчитаем целевую функцию:

F= у.е.