3 Методичні вказівки до практичних занять

Загальні тези

Мета практичних занять  засвоєння методик розрахунку реальних метрологічних характеристик вимірювальних пристроїв і установок, в тому числі граничних похибок.

Обсяг практичних занять наведений у табл. 1.1, а приблизний план проведення занять  в табл. 3.1.

Таблиця 3.1  План проведення занять

Вид роботи	Приблизний час, хв.
Перевірка присутніх і наявності виконаних домашніх завдань	5
Експрес-контроль	10
Розбір задач	50
Самостійна робота студентів	15
Видача домашніх завдань. Консультації.	10

У бібліотеці університету студент повинен отримати комплект навчально-методичної літератури [1  2] і дане видання. Навчальний посібник [1] і конспект лекцій потрібні для самостійної роботи над матеріалом дисципліни. Методичні вказівки [2] містять, крім інструкції з експлуатації приладів, рекомендації щодо розрахунку похибок вимірювань.

На початку занять викладач перевіряє наявність виконаного домашнього завдання. Кожен студент оформляє завдання індивідуально. Бажано виконувати домашнє завдання з використанням комп'ютера, дотримуючись такої послідовності:

 робота з підручником або з конспектом лекцій за відповідною темою;

 повторення матеріалу останнього практичного заняття, особливо розбір задач, розв'язаних в аудиторії;

 виконання завдань;

 перевірка розрахунків;

 пророблення контрольних запитань до наступного практичного заняття.

До роботи в аудиторії допускаються студенти, які письмово відповіли на контрольні запитання експрес-контролю. Пропущені заняття проводяться індивідуально в установленому порядку.

П р а к т и ч н е з а н я т т я № 1

РОЗРАХУНОК ПОХИБКИ ПРЯМИХ ВИМІРЮВАНЬ

1 Мета заняття

Мета заняття  набуття навичок роботи за розрахунком похибок прямого вимірювання за результатами багаторазових спостережень з урахуванням похибок апаратури.

2 Завдання на самостійну позааудиторну роботу

2.1 Дати відповіді на запитання розд. 3 [1, с.13-26; 2, с. 46-51].

2.2 Повторити порядок розрахунку граничної похибки прямого вимірювання.

2.3 Підготувати матеріали для розрахунку максимальної похибки прямого вимірювання. Мати при собі звіт до лабораторної роботи № 1.

2.4 Виписати формули для обчислення складових максимальної похибки прямого вимірювання. Особливу увагу приділити інструментальній похибці.

3 Питання до експрес-контролю

1. Визначення вимірювання, похибки, істинного і дійсного значень.

2. Визначення прямих і непрямих вимірювань.

3. Класифікація похибок.

4. Поняття похибок: абсолютна і відносна, обєктивна і субєктивна.

5. Поняття похибок: інструментальні і похибки методу, випадкові і систематичні, статичні і динамічні, грубі і промахи.

6. Формули для розрахунку середньоквадратичної похибки результатів вимірювання і спостереження.

7. Граничні значення похибок при різних законах розподілу.

8. Похибки, що підпорядковуються законам розподілу: нормальному, рівної імовірності, несиметричної рівної імовірності, трикутника (Сімпсона), арксинуса.

4 Задачі для роботи в аудиторії

Типова практична задача 5 в методичному плані розбита на декілька етапів, виділених в окремі задачі 1-5.

Задача № 1. Задано результати спостережень при вимірюванні довжини хвилі в хвилеводі _i (табл. 3.2). Знайти середнє значення _сер.

Таблиця 3.2 - Результати багаторазових спостережень довжини хвилі

в хвилеводі, мм

i	1	2	3	4	5	i = 6	7	8	9	10	11	n=12
i	40,55	40,40	40,50	40,60	40,65	40,60	40,55	40,40	40,35	40,45	40,45	40,50

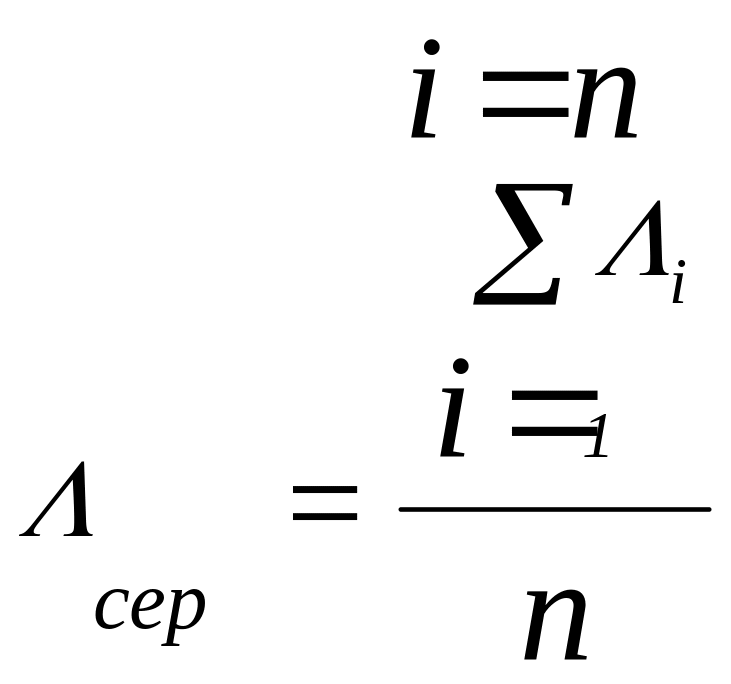= 40,50 мм.

Задача № 2. Знайти середньоквадратичну похибку результату одного спостереження, наданого в табл. 3.2.

Абсолютна середньоквадратична похибка результату одного спостереження

= 0,093 мм.

Відносна середньоквадратична похибка результату одного спостереження

 2,29510^-3 =  0,23 %.

При підсумовуванні похибок потрібно виражати похибки у безрозмірному вигляді, у відсотках.

Задача № 3. Знайти середньоквадратичну похибку результату вимірювання.

; _сер =  6,62410^-2 %  0,066 %.

Задача № 4. Розрахувати інструментальну похибку при вимірюванні довжини хвилі. Використана апаратура: генератор сигналів високочастотний Г4 – 195, підсилювач селективний У2 – 8, вимірювальна лінія Р1 – 4 (ИВЛ – 140). Характеристики зведені в табл. 3.3.

Порядок розрахунку: 1) виписати з паспортів дані про похибки (перші два стовпці табл. 3.3); 2) розрахувати відносні граничні значення похибок (третій стовп.); 3) виписати закони розподілу зазначених похибок (четвертий стовп.); 4) виписати значення коефіцієнтів закону розподілу похибок (п'ятий стовп.); 5) розрахувати приведені відносні середньоквадратичні похибки (шостий стовп.); 6) розрахувати інструментальну похибку.

Зокрема, для похибки, обумовленої нестабільністю мережі 220 В:

2,3 %.

Закон розподілу  рівної імовірності, коефіцієнт розподілу похибки К_рп = 3.

Якщо ₁ = К_рп ₁ , то 1,33%. Аналогійно знаходимо інші складові. Середньоквадратична інструментальна похибка багаторазових вимірювань дорівнює

0,05 %,

де цифрові індекси 1-6 відповідають номеру похибки, тобто номеру рядка в табл. 3.3 (похибки ₁, ₂, ₃, ₄, ₅ автоматично ввійшли в похибку _сер, як флюктуаційні).

При разовому вимірюванні інструментальна середньоквадратична похибка домінуюча і єдина, тому враховуються всі джерела інструментальних похибок:

1,72 %.

Задача № 5. Знайти середньоквадратичну і граничну похибку вимірювання довжини хвилі.

Відповідно до правила підсумовування випадкових похибок

0,08 .

З великою кількостю похибок можна припустити, що закон розподілу результуючої похибки є нормальним. Тоді

0,24 %.

При одноразовому вимірюванні  = _інстр і  =  5,2 %  в 20 разів більше!

5 Домашнє завдання

Розв'язати задачі №№ 1 – 5, змінивши початкові дані таким чином: в табл. 3.2 додати до всіх даних число 0,01 N N, де N N – дві останні цифри номера залікової книжки студента (наприклад, при N N = 12 в табл. 3.2 буде ₁ = 40,67, ₂ = 40,52, ₃ = 40,62 і т.д.), а в першому і в четвертому рядках другого стовпця табл. 3.3 додати до даних число N N (при N N=12 в першому рядку буде  17В, а в четвертому   13,5).

Таблиця 3.3  Джерела апаратурних похибок і результати розрахунків

відповідних середньоквадратичних похибок

Джерело похибки	Гранична похибка		Закон розподілу похибки	Коефіцієнт розподілу похибки KРП	i , 
	З паспорта	, 
1. Нестабільність мережі 220 В	5 В	2,27	Рівної імовірності	3	1,31
2. Установлення частоти 10 ГГц	0,01 ГГц	0,1	Рівної імовірності	3	 0,058
3. Нестабільність частоти	510-2 ГГц	0,5	Нормальний	3	0,167
4. Нестабільність потужності	1,5 розподіли 1)	 1,5	Рівної імовірності	3	0,866
5. Вихід підсилювача	2	2	Нормальний	3	0,667
6.Установка зонда вимірювальної лінії	0,05 мм	 0,12 2)	Сімпсона	2,46	 0,049
		 1 3)	Сімпсона	2,46	 0,4065
7. Вимірювання КСХ вимірювальною лінією	 2 	 2	Нормальний	3	 0,667

¹⁾ на 100 розподілів шкали індикаторного приладу.

²⁾ При вимірюванні довжини хвилі в хвилеводі.

³⁾ При вимірюванні зсуву вузла стійної хвилі.

6 Завдання підвищеної складності

Крім експериментального результату (див. домашнє завдання), довжина хвилі в прямокутному хвилеводі була розрахована за формулою

,

де   довжина хвилі в необмеженому просторі, a = 23 ^{ 0,05} мм  розмір широкої стінки хвилеводу. Визначити граничну похибку відхилення розрахункового значення  від експериментального результату.

П р а к т и ч н е з а н я т т я № 2

РОЗРАХУНОК ПОХИБКИ НЕПРЯМИХ ВИМІРЮВАНЬ

1 Мета заняття

Мета заняття  набуття навичок роботи з розрахунку похибок непрямого вимірювання за результатами багаторазових спостережень з урахуванням коефіцієнтів впливу і похибок апаратури.

2 Завдання на самостійну позааудиторну роботу

2.1 Дати відповіді на запитання розд. 3 [1, с.13-26; 2, с. 46-51].

2.2 Повторити порядок розрахунку граничної похибки непрямого вимірювання.

2.3 Підготовити матеріали для розрахунку максимальної похибки непрямого вимірювання. Мати при собі звіт до лабораторної роботи № 3.

2.4 Виписати формули для обчислення складових максимальної похибки непрямого вимірювання. Особливу увагу приділити розрахунку коефіцієнтів впливу.

3 Питання до експрес-контролю

1. Визначення вимірювання, похибки, істинного і дійсного значень, прямих і непрямих вимірювань.

2. Класифікація похибок. Поняття похибок: абсолютна і відносна, обєктивна і субєктивна. Поняття похибок: інструментальні і похибки методу, випадкові і систематичні, статичні і динамічні, грубі та промахи.

3.Формули для розрахунку середньоквадратичної похибки результату вимірювання і результату спостереження. Поняття приведеної похибки.

4. Граничні значення похибок при різних законах розподілу. Похибки, піпорядковані законам розподілу: нормальному, рівної імовірності, несиметричної рівної імовірності, трикутника (Сімпсона), арксинуса (арккосинуса).

5. Похибки непрямих вимірювань. Коефіцієнти впливу.

6. Методика підсумовування окремих похибок в області радіотехнічних вимірювань.

4 Задачі для роботи в аудиторії

Розглянемо коротко необхідні теоретичні відомості.

Повний (комплексний) опір

визначений чисельно, якщо відомі складові R і X або модуль та аргумент .

Для комплексної провідності

.

При вимірюванні повного опору складових похибок багато, тому закон розподілу граничної похибки  можна прийняти нормальним. Тоді

Приведена середньоквадратична похибка непрямого виміру параметра , яка входить до формули для розрахунку скінченної величини F, визначається з урахуванням коефіцієнтів впливу K^F_, що обчислюються за формулою

Приведені середньоквадратичні похибки будуть рівні:

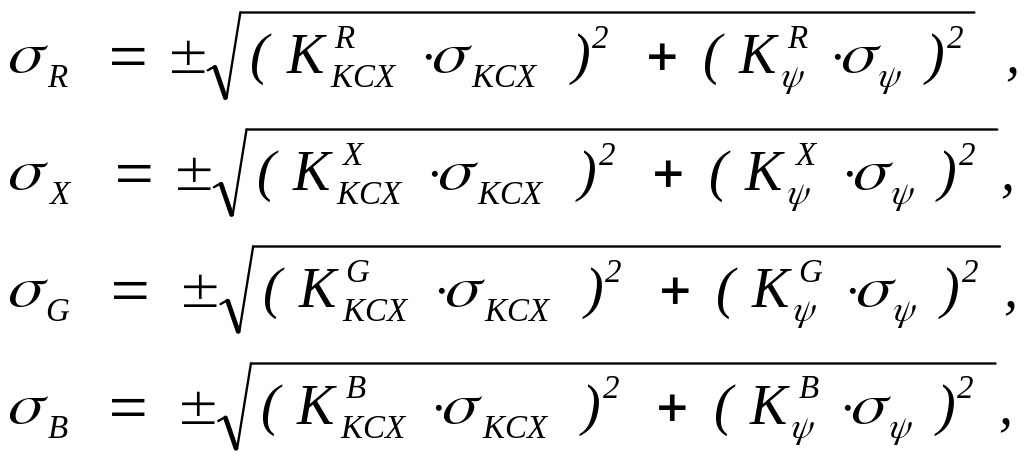
де _КСХ – відносна середньоквадратична похибка вимірювання КСХ;

_  відносна середньоквадратична похибка вимірювання .

Формули для розрахунку нормованих складових зведені в табл. 3.6, а формули для розрахунку коефіцієнтів впливу  у табл. 3.7.

Таблиця 3.6  Формули для розрахунку складових нормованого повного опору

або нормованої повної провідності

Параметр	Формула
Повний опір
Повна провідність

Таблиця 3.7  Формули для розрахунку коефіцієнтів впливу

Вимірювана величина		Параметр впливу	Формула
Повний опір (4.1)		R'н
		X'н
	Z	R'н
		X'н
	R'н	КСХ
		
	X'н	КСВ
		
Повна провідність (4.4)		G'н
		B'н
	Y	G'н	`
		B'н
	G'н	КСХ
		
	B'н	КСХ
		

Задача № 1. Отримати формулу для розрахунку коефіцієнта впливу по КСХ для розрахунку похибки вимірювання R_н.

Запишемо

Похідна ,

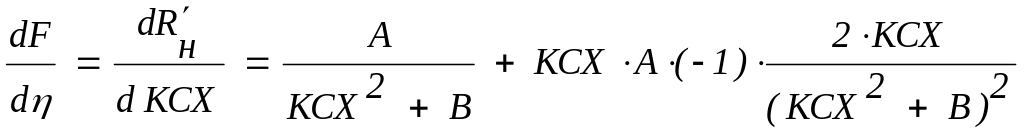Остання формула - відповідь.

Задача № 2 . Отримати формулу для розрахунку коефіцієнта впливу по _н для розрахунку похибки вимірювання R_н.

Після множення на необхідний коефіцієнт отримаємо

Задача № 3. Вимірюваним значенням КСХ = 1,5 и _н = 1,1 рад відповідають значення приведених середньоквадратичних похибок _КСХ =  2,2  і _ =  3,3 . З урахуванням результатів задач 1, 2 знайти приведену середньоквадратичну похибку вимірювання R_н і значення максимальної похибки.

Результати розрахунків:

_R =  2,72  , _R =  8,15    8,2  .

5 Домашнє завдання

Вивести формули для розрахунку коефіцієнтів впливу і знайти приведену середньоквадратичну і максимальну похибки вимірювання реактивної складової повного опору.

Числові значення взяти із задачі № 3, додавши до всіх даних число 0,01 N N, де N N – дві останні цифри номера залікової книжки студента. Наприклад, при N N = 33 маємо КСХ = 1,83, _н = 1,43 рад, _КСХ =  2,53  і _ =  3,63 .

6 Завдання підвищеної складності

Розрахувати максимальну похибку непрямого вимірювання хвильового опору несиметричної стрічкової лінії передачі (в квазістатичному наближенні) за результатами прямих вимірювань відносної діелектричної проникності  = (NN+1)  5, товщини діелектрика h = 1 мм  (NN/5) і ширини металевої стрічки w = (0,9 - 0,01NN)  0,02 мм.

П р а к т и ч н е з а н я т т я № 3

ОЦІНКА ВИПАДКОВОЇ ПОХИБКИ АНАЛІТИЧНИМ ШЛЯХОМ

1 Мета заняття

Мета заняття  набуття навичок розрахунку випадкової похибки аналітичним шляхом з урахуванням екстремумів або заданого рівня фізичної величини.

2 Завдання на самостійну позааудиторну роботу

2.1 Дати відповіді на запитання розд. 3 [1, с.20-26].

2.2 Повторити порядок розрахунку граничної випадкової похибки прямого вимірювання.

2.3 Повторити порядок розрахунку граничної випадкової похибки непрямого вимірювання.

2.4 Виписати формули для знаходження похідних елементарних функцій.

2.5 Підготувати формули для обчислення розподілу поперечної складової електричного поля стійної хвилі в лінії передачі.

3 Питання до експрес-контролю

1. Поняття випадкової і систематичної похибки.

2. Порядок розрахунку граничної випадкової похибки прямого вимірювання.

3. Порядок розрахунку граничної випадкової похибки непрямого вимірювання.

4. Граничні значення похибок при різних законах розподілу. Похибки, що підлягають законам розподілу: нормальному, рівної імовірності, несиметричної рівної імовірності, трикутника (Сімпсона), арксинуса (арккосинуса).

5. Методика підсумовування окремих похибок в області радіотехнічних вимірювань.

4 Задачі для роботи в аудиторії

У даному варіанті відсутні результати багаторазових спостережень. Оцінка випадкової похибки виконується шляхом розрахунку значення вимірювальної величини біля екстремального або біля заданого рівня.

Е кспериментально або теоретично знайдена залежність показань вимірювального пристрою  від вимірювальної величини , яка має вигляд

 = f().

Необхідно знайти похибку , обумовлену роздільною здатністю відлікового пристрою  (рис. 3.1).

Розглянемо знаходження похибки в точці екстремуму. Функцію f(), якщо вона в

Рисунок 3.1  Похибка в екстремумі точці екстремуму _е неперервна і має всі

похідні, можна розкласти в ряд Тейлора:

Обмежуючись трьома членами розкладання і враховуючи, що в екстремум , отримаємо

,

звідки

.

З а умови відсутності екстремуму   _е і в точці  = ₀ по рис. 3.2  = ₀. В цій точці перша похідна . Обмежуючись двома членами розкладання в ряд, отримаємо

,

тобто

.

В обох випадках отримали формули, які Рисунок 3.2  Похибка наданого рівня

зв'язують межу випадкової похибки і роздільну

здатність приладу.

Задача № 1. Вимірюється розподіл електричного поля вздовж неузгодженої лінії передачі. Знайти похибку вимірювання пересування головки вимірювальної лінії,

я ка відповідає роздільній здатності приладу в максимумі стійної хвилі при квадратичній характеристиці детектора індикаторної головки.

Рисунок 3.3  Графіки частково стійних хвиль

З курсу технічної електродинаміки: при квадратичній характеристиці детектора вимірювальної лінії показання індикаторного приладу  змінюються за законом

,

де ₁  показання в режимі біжної хвилі ( = 0),   коефіцієнт відбиття,   коефіцієнт фази, l  відстань від навантаження в бік генератора (рис. 3.3). Необхідно знайти другу похідну.

Перша похідна

.

Друга похідна

.

У максимумі стійної хвилі , тому

.

Якщо в максимумі стійної хвилі відлік приладу _max, то ₁ = _max/(1+)². Тоді

.

Нехай прилад має _max = 100 розподілок шкали з градацією  =1:

,

де КСХ  коефіцієнт стійної хвилі.

Для розрахунку приймемо  = 40 мм. В режимі короткого замикання  = 1, l = 0,64 мм. При КСХ = 1,2 коефіцієнт відбиття  = 0,091, граничне значення похибки l = 1,15 мм.

Задача № 2. Знайти похибку вимірювання пересування головки вимірювальної лінії, яка відповідає роздільній здатності приладу в мінімумі стійної хвилі.

Без коментарів:

і кінцева формула матиме такий самий вигляд.

Задача № 3. Знайти похибку вимірювання пересування головки вимірювальної лінії, яка відповідає роздільній здатності приладу посередині між екстремумами стійної лінії.

У даній точці екстремуми відсутні, тому

.

Для  = 40 мм, _max = 100 і  =1 .

При короткому замиканні l = 0,032 мм, а при КСХ = 1,2  l = 0,177 мм.

5 Домашнє завдання

Розв'язати задачі № 1-3 при лінійній характеристиці детектора індикаторної головки хвилеводної вимірювальної лінії, коли  = 0,02 N N та

.

6 Завдання підвищеної складності

Знайти похибку вимірювання нормованої діаграми спрямованості решітки з NN+1 однакових неспрямованих випромінювачів з відсутніми зсувами фази між ними, розташованих на відстані у півхвилі один від одного, яка при лінійній характеристиці детектора відповідає роздільній здатності приладу для вимірювання кута повороту в напрямку: а) головної пелюстки; б) першого мінімуму; в) найменшої бокової пелюстки.

П р а к т и ч н е з а н я т т я № 4

АНАЛІЗ ОСОБЛИВОСТЕЙ СИСТЕМАТИЧНИХ ПОХИБОК

1 Мета заняття

Мета заняття  набуття навичок оцінки систематичних похибок розрахунковим шляхом.

2 Завдання на самостійну позааудиторну роботу

2.1 Дати відповіді на запитання розд. 3 [1, с.26-31].

2.2 Повторити матеріал стосовно імовірності появи похибки в конкретному інтервалі.

2.3 Законспектувати основні способи виявлення, оцінки і виключення систематичних похибок.

3 Питання до експрес-контролю

1. Поняття систематичної і випадкової похибки.

2. Граничні значення похибок при різних законах розподілу. Похибки, що підпорядковуються законам розподілу: нормальному, рівної імовірності, несиметричної рівної імовірності, трикутника (Сімпсона), арксинуса (арккосинуса).

3. Методика підсумовування похибок в області радіотехнічних вимірювань.

4. Способи оцінки і виключення систематичних похибок.

5. Обгрунтування функції розподілу систематичної похибки.

4 Задачі для роботи в аудиторії

Основні способи виявлення, оцінки і виключення систематичних похибок _сист такі: 1) виявлення _сист шляхом багаторазових вимірювань двома різними методами; 2) оцінка _сист при використанні більш точного методу або більш точного засобу вимірювання; 3) оцінка _сист аналітичним шляхом; 4) виключення _сист при вимірюванні спеціальними методами, наприклад, методом компенсації за знаком похибки; 5) введення поправки; 6) розрахунок функції розподілу _сист. Розглянемо третій і шостий варіанти.

З адача № 1. На рис. 3.4 зображена найпростіша схема замкненого контуру, у якому вимірюється сила струму. Необхідно оцінити систематичну похибку, обумовлену власним опором амперметра r_A (рис. 3.5).

Рисунок 3.4  Схема без вимірювальної апаратури

Рисунок 3.5  Схема з вимірювальною апаратурою

На схемі за рис. 3.4 істинне значення сили струму

,

а з урахуванням опору амперметра за рис. 3.5

.

Систематична похибка

.

Задача № 2. Розрахувати функцію розподілу систематичної похибки .

Імовірності попадання значень випадкової величини x до інтервалу x, а випадкової величини y до інтервалу y дорівнюють

,

де  густини розподілу імовірностей. При однаковій імовірності і

.

Для рівномірного закону

.

Максимальне значення систематичної похибки _сист =  h, при цьому випадкова величина  розподілена рівномірно в інтервалі -/2    +/2. Тому

.

Похідна

і ,

а бо .

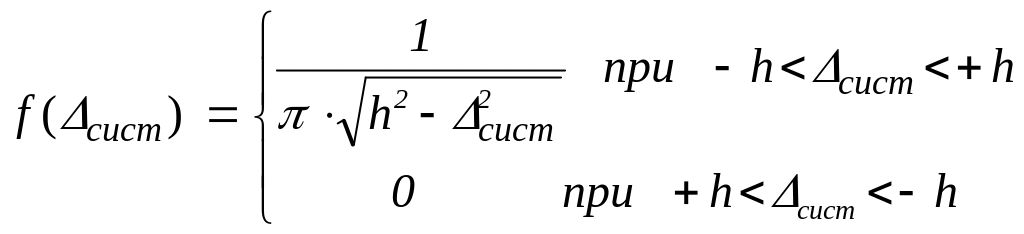Розподіл арксинуса (або U-розподіл) зображено на рис. 3.6.

Доповнюючи задачу, знайдемо дисперсію і середньоквадратичну похибку .

Математичне сподівання M[_сист] = 0.

Рисунок 3.6  Розподіл арксинуса

Тому

.

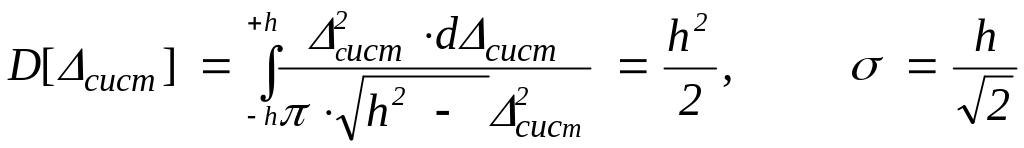Під кінець розглянемо менший інтервал h₁. Довірча імовірність

.

Результати розрахунків подані в табл. 3.8.

Таблиця 3.8  Значення довірчої імовірності в різних інтервалах

h1/h	0,2	0,4	0,6	0,8	1,0
P(-h1<сист<+h1)	0,128	0,262	0,410	0,590	1,0

5 Домашнє завдання

5.1 В задачі № 1 прийняти значення , . Внести поправку, перевести систематичну похибку до розряду випадкових, розрахувати відповідні значення граничної та середньоквадратичної похибок.

5.2 Розв'язати задачу № 2 відносно систематичної похибки .

6 Завдання підвищеної складності

Розрахувати значення довірчої імовірності в інтервалі  NN/2 для систематичної похибки , де h = NN.