
- •Тема 3.2. Средние величины и показатели вариации
- •1.Понятие средней величины
- •2. Средняя арифметическая
- •3. Свойства средней арифметической
- •4.Средняя гармоническая
- •5. Критерий выбора вида средней в экономических расчетах
- •6. Средняя квадратическая и средняя геометрическая
- •7. Описательные (структурные) средние
- •8. Показатели вариации
- •Тема 3.3 Ряды динамики и индексы.
- •1. Понятие и виды рядов динамики
- •2. Показатели анализа рядов динамики
- •3.Способы преобразования рядов динамики
- •4.Понятие об индексах.
- •5.Индивидуальные индексы
- •6.Общие индексы
- •7.Индекс переменного состава.
- •8.Индекс постоянного состава.
- •9.Индекс влияния структурных сдвигов.
- •Раздел 4.Тема 4.1 Выборочное наблюдение Тема 4.2 Оценка результатов выборочного наблюдения
- •1. Сущность выборочного наблюдения
- •2.Ошибки выборочного наблюдения.
- •3.Виды выборочного наблюдения.
- •4. Ошибки выборки
- •5.Определение необходимой численности выборки
- •Раздел 5 Тема 5.1 Изучение статистической связи между явлениями
- •1.Виды зависимости между явлениями
- •2. Корреляционный анализ
- •3. Регрессионный анализ
Раздел 4.Тема 4.1 Выборочное наблюдение Тема 4.2 Оценка результатов выборочного наблюдения
1. Сущность выборочного наблюдения
2.Ошибки выборочного наблюдения.
3.Виды выборочного наблюдения.
4. Ошибки выборки
5.Определение необходимой численности выборки
1. Сущность выборочного наблюдения
Выборочное наблюдение – это вид несплошного наблюдения, который основан на теории вероятности и математической статистике.
Основные понятия выборочного наблюдения:
генеральная совокупность – это совокупность, подлежащая изучению или наблюдению (N);
выборочная совокупность – это совокупность, подвергшаяся непосредственному наблюдению. Она выбирается из генеральной совокупности в порядке случайного, типического, серийного и механического отборов (n);
генеральная
средняя
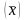 ,
т.е. это средняя, рассчитанная для всей
изучаемой генеральной совокупности;
,
т.е. это средняя, рассчитанная для всей
изучаемой генеральной совокупности;
выборочная
средняя
 – это средняя, исчисленная для выборочной
совокупности;
– это средняя, исчисленная для выборочной
совокупности;
генеральная
доля
 – это доля единиц совокупности, обладающих
данным признаком во всей генеральной
совокупности, например, доля брака во
всей произведенной продукции (генеральной
совокупности);
– это доля единиц совокупности, обладающих
данным признаком во всей генеральной
совокупности, например, доля брака во
всей произведенной продукции (генеральной
совокупности);
выборочная
доля
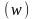 – доля признака в выборочной совокупности.
– доля признака в выборочной совокупности.
2.Ошибки выборочного наблюдения.
При проведении выборочного наблюдения могут возникать ошибки регистрации (случайные и систематические) и ошибки репрезентативности (представительности).
1). При наличии систематических ошибок сплошное наблюдение дает менее точный результат. В этом случае выборочное наблюдение можно использовать в качестве контроля данных сплошного наблюдения
2). Если систематические ошибки не возникают, то более точный результат дает сплошное наблюдение. В этом случае выборочное наблюдение может быть использовано с целью экономии затрат труда и средств при условии, что сможем определить с достаточной точностью ошибку репрезентативности.
3.Виды выборочного наблюдения.
Организация выборочного наблюдения может быть разнообразна как по схемам, так и по методам проведения. Различают две схемы проведения выборочного наблюдения:
1. Повторной называется выборка, когда единицы генеральной совокупности, отобранные в выборочную совокупность, после их изучения или обследования возвращаются обратно в генеральную совокупность. При таком способе объем генеральной совокупности не изменяется. При этом одна и та же единица генеральной совокупности может повторно попасть под обследование.
2. Бесповторный называется выборка, при которой единицы генеральной совокупности, отобранные в состав выборочной совокупности, обратно в генеральную после обследования не возвращаются. При этом способе объем генеральной совокупности сокращается и каждая единица генеральной совокупности может быть отобрана в выборочную только один раз.
И повторная, и бесповторная выборки могут производиться следующими способами:
Случайный отбор (случайная выборка).
Типический отбор.
Серийный (гнездовой) отбор.
Только бесповторной выборке присущ способ механического отбора.
4. Ошибки выборки
1) Средняя ошибка выборки показывает: на сколько в среднем возможные варианты выборочных средних отклоняются от их генеральной средней.
Средняя ошибка выборки для среднего значения признака при повторном отборе:
|
|
где
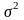 –
дисперсия признака в выборочной
совокупности
–
дисперсия признака в выборочной
совокупности
n – объем выборочной совокупности.
Средняя ошибка для среднего значения признака при бесповоротном отборе:
|
|
где
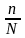 –
доля выборки в генеральной совокупности.
–
доля выборки в генеральной совокупности.
Средняя ошибка для доли признака при повторном отборе:
|
|
Средняя ошибка для доли признака при бесповторном отборе:
|
|
2)Предельной называется максимальная ошибка выборки, которую можно гарантировать при заданном уровне вероятности. Она определяется по формуле:
|
|
Предельная ошибка для среднего значения признака при повторном способе отбора:
|
|
Предельная ошибка выборки для среднего значения признака при бесповторном отборе:
|
|
Предельная ошибка для доли признака при повторном отборе:
|
|
Предельная ошибка для доли признака при бесповторном отборе:
|
|

 ,
,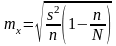 ,
, .
. .
.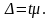
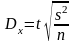 .
. .
.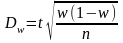 .
.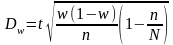 .
.