Тема 3.2. Средние величины и показатели вариации

1.Понятие средней величины

2.Средняя арифметическая

3.Свойства средней арифметической

4.Средняя гармоническая

5.Критерий выбора вида средней в экономических расчетах

6.Средняя квадратическая и средняя геометрическая

7.Описательные (структурные) средние

8.Показатели вариации

Задание для внеаудиторной самостоятельной работы № 7:

1.Расчёт моды и медианы в интервальном вариационном ряду.

1.Понятие средней величины

Средняя величина – обобщающий показатель, выражающий типичный уровень (размер) варьирующего признака в расчете на единицу однородной совокупности.

Средняя величина относится к числу обобщающих показателей. Она отражает общие черты, общие закономерности.

Метод средних – один из главных в статистике.

Принципы вычисления средних величин:

1) средняя величина может быть рассчитана не для любого множества, а лишь для качественно однородных совокупностей;

2) средняя величина должна давать качественно-количественную характеристику изучаемому явлению.

Задачи, решаемые с помощью средних величин:

• характеристика уровня развития явления,

• сравнение двух или нескольких уровней,

• характеристика изменения уровня во времени,

• выявление и характеристика связей явлений и др.

2. Средняя арифметическая

средняя арифметическая простая:

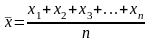или в общем виде: = ,

где x – значения варьирующего признака,

n – число этих значений (число единиц совокупности),

- сигма, знак суммирования.

Базой для вычисления этой формы средней служат первичные записи результатов наблюдений.

средняя арифметическая взвешенная:

Если известны значения признака, каждое из которых повторяется различное число раз, то для определения средней применяется формула:

или = , или = ,

где m - частота – веса (абсолютные показатели),

f – частости – веса (относительные показатели – удельные веса в % ),

Основой для вычисления средней арифметической взвешенной является обработанный материал, т.е. сгруппированные данные.

3. Свойства средней арифметической

1. Алгебраическая сумма отклонений всех вариант( x) от их средней арифметической ( )равна нулю. .

2. Если все варианты (x) уменьшить или увеличить на какое-то постоянное число (а), средняя арифметическая ( ) уменьшится или увеличится на то же самое число (т. е. будет равно 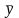). Если , то .

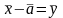3. Если все варианты (x) уменьшить или увеличить в одно и то же число раз (b), средняя арифметическая ( ) уменьшится или увеличится в то же самое число раз. Если 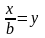, то .

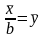4. Если веса (m) средней арифметической ( ) уменьшить или увеличить в несколько раз (k), средняя арифметическая не изменится

4.Средняя гармоническая

Простая: .

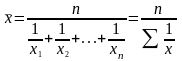Взвешенная: .

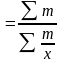5. Критерий выбора вида средней в экономических расчетах

В экономических расчетах наиболее часто используются два вида средних: средняя арифметическая или средняя гармоническая. Выбор того или иного вида средней зависит от имеющихся данных и исходного отношения (соотношения) – логической (словесной) формулы средней.

Исходное отношение составляется на основе теоретического и экономического анализа. Примеры составления исходных отношений:

Средняя урожайность (ц/га) = ,

средний размер вклада в банке = .
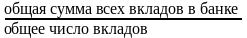