3. Определение спектральной плотности случайного процесса

Для вычисления спектральной плотности стационарного случайного процесса используется следующая формула:

.

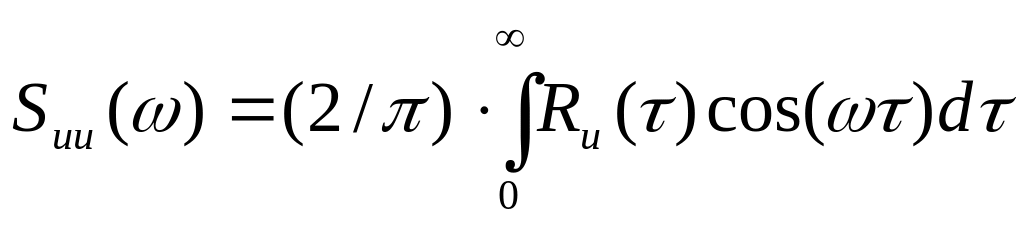Формула для вычисления функции автокорреляции имеет следующий вид:

.

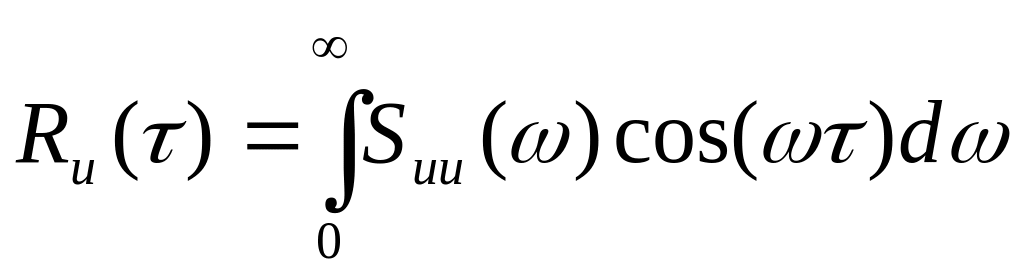Корреляционная функция и спектральная плотность подчинены закономерности: чем протяженнее кривая , тем уже корреляционная функция , и наоборот.

Формула для вычисления дисперсии имеет следующий вид:

.

Контрольные вопросы

1.Что понимают под выражением “случайный сигнал”?

2.Вероятностные характеристики случайных сигналов.

3.Числовые характеристики случайных сигналов.

4.Каков физический смысл среднеквадратического ожидания?

5.В чём различие числовых характеристик для дискретных и непрерывных случайных сигналов?

Лабораторная работа № 3

“Преобразование непрерывных сигналов в дискретные”.

Цель. Преобразование непрерывных сигналов в дискретные, а также:

Задание.

1) Определение шага равномерной дискретизации с помощью интерполирующих многочленов Лагранжа.

а) Интерполирующие многочлены Лагранжа нулевой степени

Определить шаг равномерной дискретизации на основе интерполирующих многочленов нулевой степени на примере рассмотрения некоторого гармонического сигнала вида и значения погрешности дискретизации .

б) Интерполирующие многочлены Лагранжа первой степени

Определить шаг равномерной дискретизации на основе интерполирующих многочленов первой степени на примере рассмотрения некоторого гармонического сигнала вида и значения погрешности дискретизации .

Нарисовать график дискретизации сигнала с помощью многочлена Лагранжа и вычислить несколько значений шага дискретизации при различных значениях параметров сигнала и ошибки дискретизации.

2) Определение шага равномерной дискретизации с помощью экстраполирующих многочленов Тейлора.

а) Экстраполирующие многочлены Тейлора нулевой степени

Определить шаг равномерной дискретизации на основе экстраполирующих многочленов нулевой степени на примере рассмотрения гармонического сигнала и значения погрешности дискретизации .

б) Экстраполирующие многочлены Тейлора первой степени

Определить шаг равномерной дискретизации на основе экстраполирующих многочленов первой степени на примере рассмотрения гармонического сигнала и значения погрешности дискретизации .

Нарисовать график дискретизации сигнала с помощью многочлена Тейлора и вычислить несколько значений шага дискретизации при различных значениях параметров сигнала и ошибки дискретизации

3) Исследование адаптивной дискретизации.

а) Адаптивная дискретизация реализации сигнала с использованием многочлена нулевой степени

Провести адаптивную дискретизацию на примере гармонического сигнала с помощью аппроксимации многочлена нулевой степени вида при значении наибольшего отклонения от равного .

Нарисовать график адаптивной дискретизации для определения параметров , , и отметить достоинства и недостатки адаптивной дискретизации.

Отчет по лабораторной работе для каждого пункта должен содержать:

- цель и задание.

- краткие теоретические сведения.

- различные варианты входных данных и графики для них.

- выводы.

Основные понятия и определения.

На современном этапе развития информационной техники предпочтение отдается дискретным сигналам, поэтому непрерывные сигналы, как правило, преобразуются в дискретные. С этой целью каждый непрерывный сигнал подвергается операциям квантования по времени (дискретизации) и по уровню.

Дискретизация - преобразование функции непрерывного времени в функцию дискретного времени, представляемую совокупностью величин, называемых координатами, по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью. Роль координат часто выполняют мгновенные значения функции, отсчитанные в определенные моменты времени.

Квантование - преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений. Оно сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования.

Для конкретных задач управления или исследования какого-либо объекта обычно требуется значительно меньше информации, чем ее поступает с датчиков виде сигналов, изменяющихся во времени непрерывно. Учет сведений об этих сигналах и целях их получения позволяет ограничиться отсчетами, взятыми через определенные моменты времени.

При неизбежных колебаниях во времени интересующих нас параметров и конечной погрешности средств измерения информация о величине сигнала в каждый момент отсчета всегда ограничена, что и выражается в конечном числе уровней квантования. Кроме того, специфика решаемых в системе задач часто такова, что целесообразно ограничиться значительно меньшим числом уровней, чем следует из указанных выше ограничений.

Во многих случаях информация извлекается и передается с целью дальнейшей обработки средствами цифровой техники, в первую очередь ЭВМ и микропроцессорами. Рациональное выполнение операций дискретизации и квантования при этом приводит к значительному экономическому эффекту как за счет снижения затрат на хранение и обработку получаемой информации, так и вследствие сокращения времени обработки информации, что ведет к улучшению качества управления.

При передаче и обработке информации в цифровой технике существует принципиальная возможность снижения вероятности получения ошибочного результата до весьма малых значений.

Она возникает потому, что при использовании дискретных сигналов, во-первых, применимы такие методы кодирования, которые обеспечивают обнаружение и исправление ошибок, а, во-вторых, можно избежать свойственного аналоговым сигналам эффекта накопления искажений в процессе их передачи и обработки, поскольку квантованный сигнал легко восстановить до первоначального уровня всякий раз, когда величина накопленных искажений приблизится к половине кванта. Практическая реализация указанных методов наиболее эффективна при минимальном числе уровней, равном двум.

Выражение информации в цифровой форме облегчает унификацию операций ее преобразования на всех этапах обращения. Массовость изготовления типовых узлов и блоков, простота их настройки, отсутствие необходимости регулировки в процессе эксплуатации позволят, в свою очередь, улучшить такие важнейшие технико-экономические показатели средств цифровой техники, как стоимость изготовления и эксплуатации, а также надежность.