3. Распределение энергии в спектре периодических сигналов.
При
рассмотрении распределения мощности
в спектре периодического сигнала под
временной функцией будет пониматься
ток
,
протекающий по резистору
с периодом изменения
.
Средняя мощность, выделяемая на резисторе , описывается следующим выражением:
,
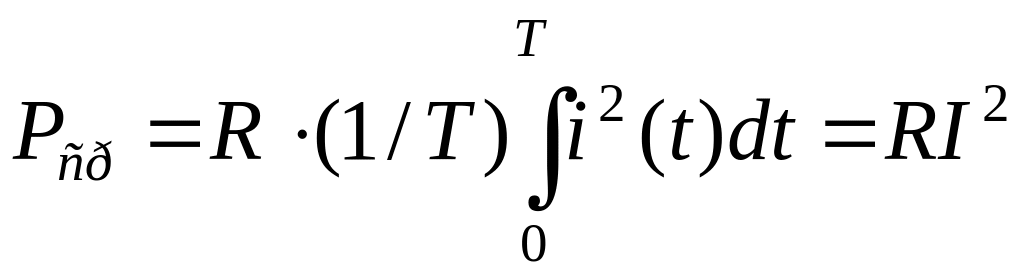где
- квадрат действующего значения тока.
Представив ток рядом Фурье, получим следующее выражение для квадрата действующего значения тока:
.
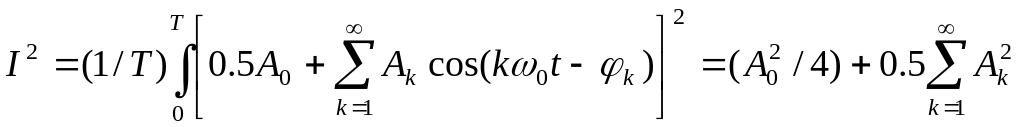Следовательно, средняя мощность
.
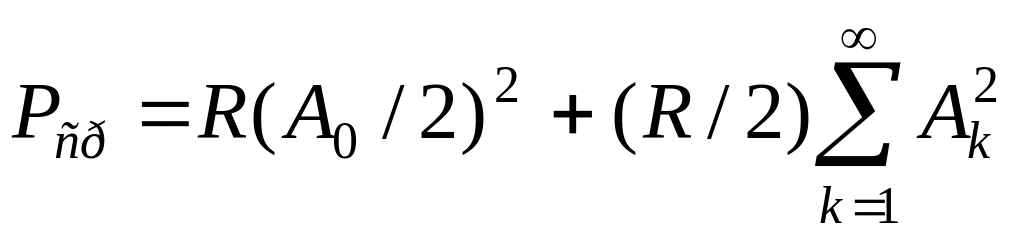Таким образом, средняя мощность, выделяемая сложным периодическим током в резисторе, равна сумме средних мощностей, выделяемых в этом резисторе отдельными гармониками и его постоянной составляющей. С течением времени выделяемая энергия безгранично растет, при этом средняя мощность остается постоянной и не зависит от фаз отдельных гармоник и, следовательно, будет сохранять свое значение при изменениях формы сигнала, обусловленных нарушениями фазовых соотношений гармоник спектра.
3.1. Исследование спектров непериодических сигналов.
Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т.е.
,
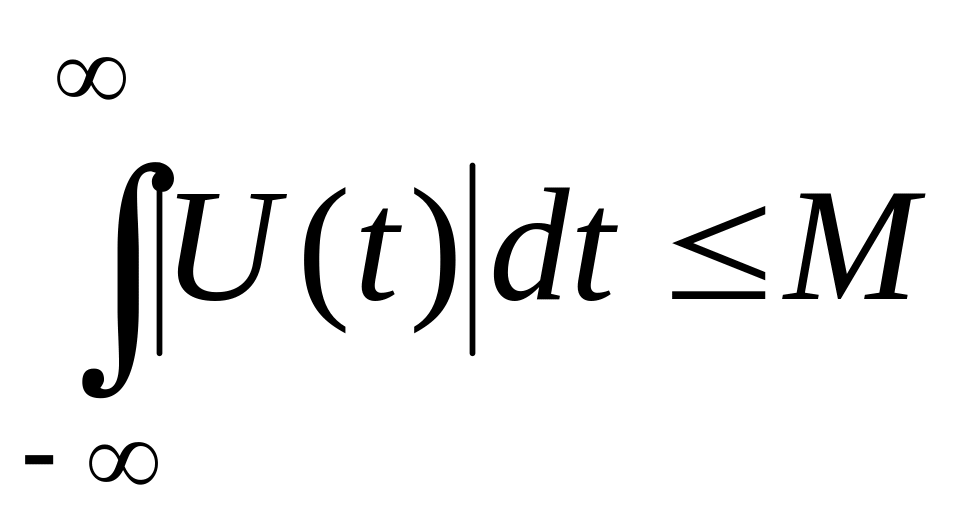где
- конечная величина.
Пару
преобразований Фурье для периодической
функции
запишем в виде:
,
.
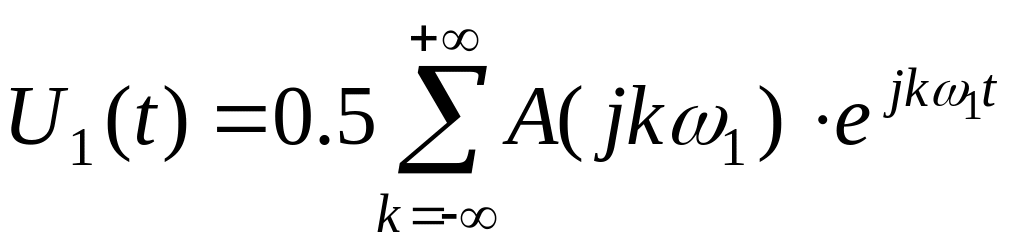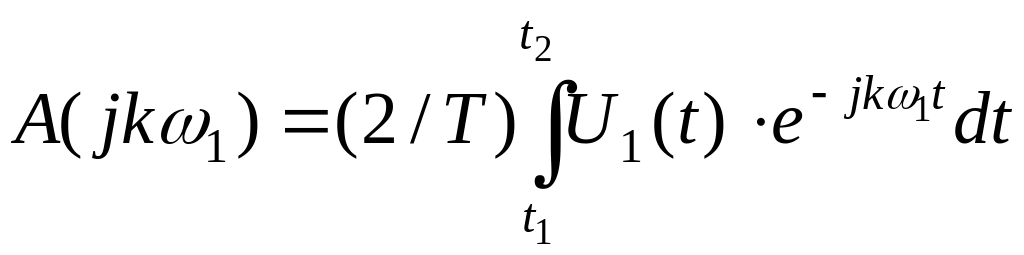При
переходит в
,
частота
уменьшается до
,
а
превращается в текущую частоту
.
Заменяя суммирование интегрированием,
находим
:
.
Обозначив
интеграл в квадратных скобках
,
получим формулы для прямого и обратного
преобразования Фурье:
,
.
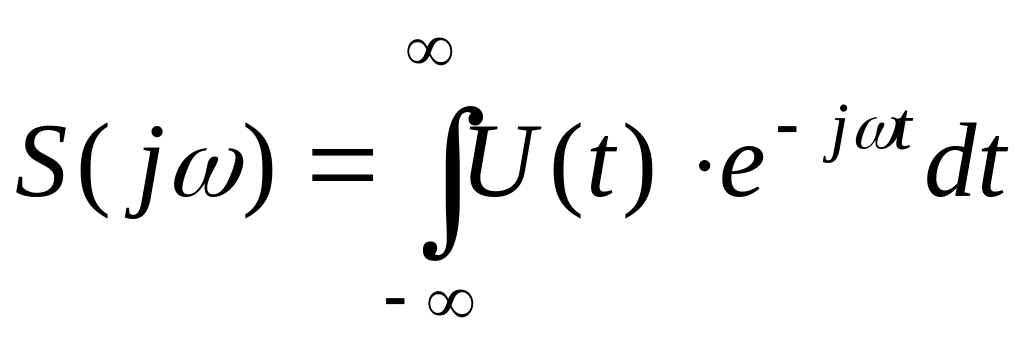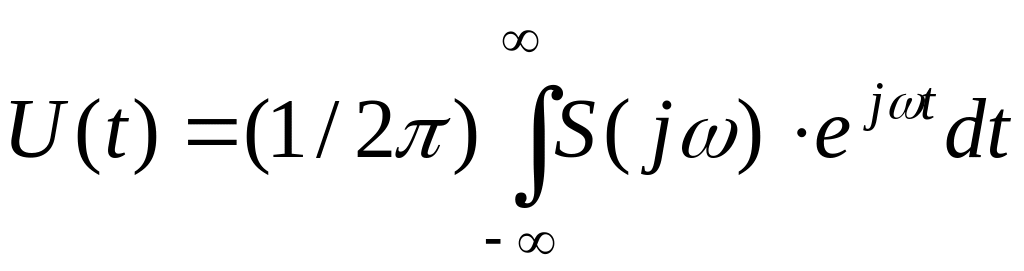Величина называется комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда / частота].
Как комплексная величина спектральная характеристика может быть записана в виде:
,
где
называется спектральной плотностью
амплитуд или спектром непериодического
сигнала.
Так как составляющие спектральные составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику, состоящую из действительной и мнимой частей:
,
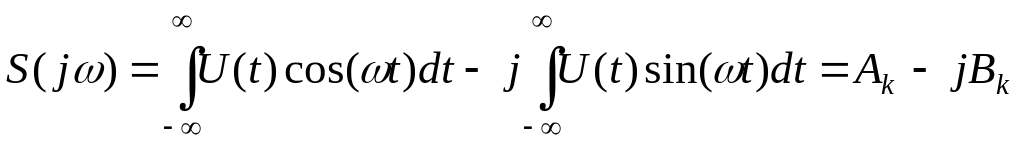где
;
.
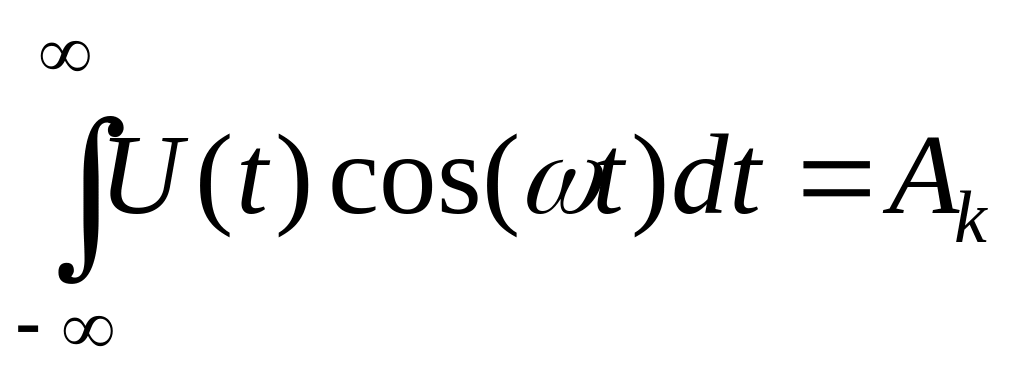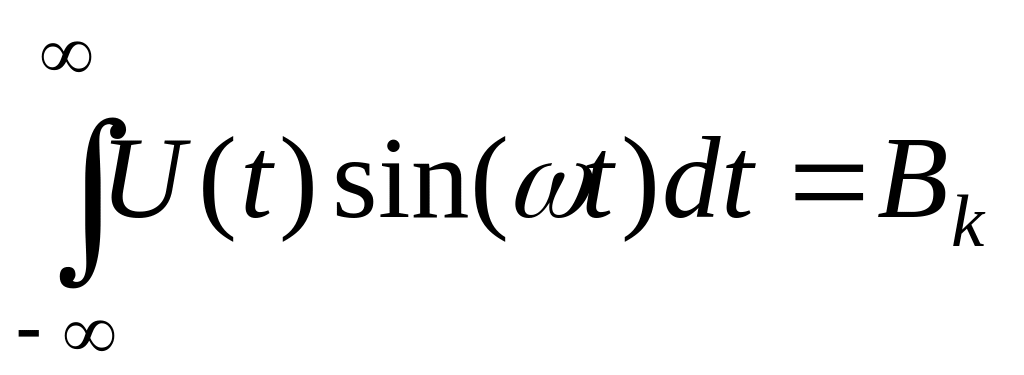Модуль
спектральной характеристики
определяется
выражением
и представляет собой четную функцию частоты. Для фазы спектральной характеристики соответственно получаем
.
Перейдем от комплексной формы интегрального преобразования Фурье к тригонометрической и окончательно получим:
.
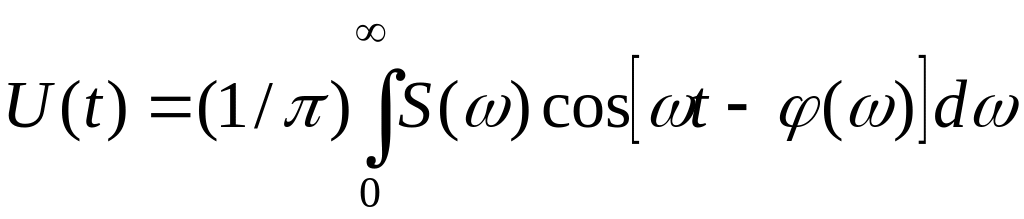Контрольные вопросы
1.В чём отличие случайных сигналов от детерминированных?
2.Спектральная плотность одиночного прямоугольного импульса?
3.Определить, какая часть средней мощности, выделяемая резистором с сопротивлением , периодической последовательностью прямоугольных импульсов приходится на девятую гармонику ряда Фурье.
4.Что представляет собой частотный спектр непрерывного сигнала?
5.Свойства дельта-функции.
6.Изменение формы фазового спектра сигнала при смещении его относительно временной оси.