2. Исследование спектров периодических сигналов.
При анализе сигналов в установившемся режиме можно исходить из предположения, что сигналы исследуемые существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени.
Пусть
функция
,
заданная в интервале времени
и удовлетворяющая условиям Дирихле,
повторяется с периодом
на протяжении времени от -
до +.
Условия Дирихле: на любом конечном
интервале функция должна быть непрерывной
или иметь конечное число точек разрыва
первого рода, а также конечное число
экстремальных точек; в точках разрыва
функцию
следует считать равной
.
В качестве базисных функций выбираются экспоненциальные функции, тогда результирующий, сложный сигнал представляется как сумма базисных функций:
,
(1.2.1)
,
(1.2.2)
Соотношение
(1.2.1) представляет собой ряд Фурье в
комплексной форме, содержащий
экспоненциальные функции с положительным
и с отрицательным параметром
(двустороннее частотное представление).
Составляющие с отрицательными частотами
являются следствием комплексной формы
записи вещественной функции.
Функция
называется комплексным спектром
периодического сигнала
.
Этот спектр имеет дискретный характер,
так как функция
определена на числовой оси только для
целых значений
.
Значение функции
при конкретном значении
называется комплексной амплитудой.
Огибающая
комплексного спектра
имеет вид:
.
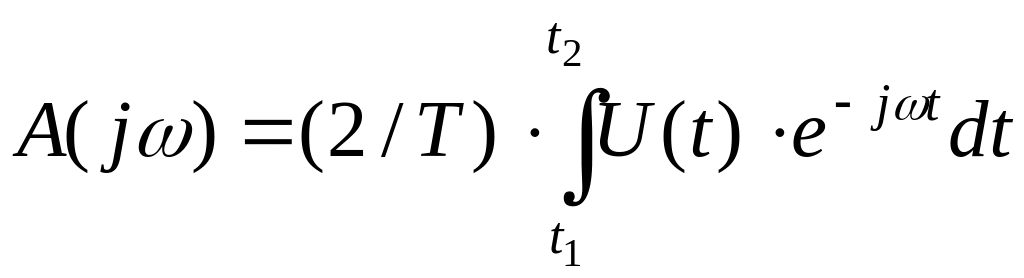Комплексный спектр можно записать в форме:
.
Модуль
комплексного спектра
называется спектр амплитуд, а функция
- спектр фаз.
Если известны спектр амплитуд и спектр фаз сигнала, то в соответствии с (1.2.1) он восстанавливается однозначно. В практических приложениях более значимым является спектр амплитуд, а информация о фазах составляющих часто несущественна.
Поскольку и отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.
По формуле Эйлера
можно
выразить комплексный спектр
в виде действительной и мнимой частей:
,
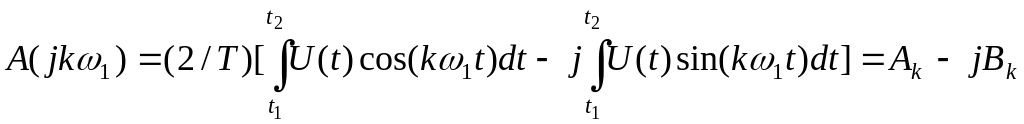где
;
.
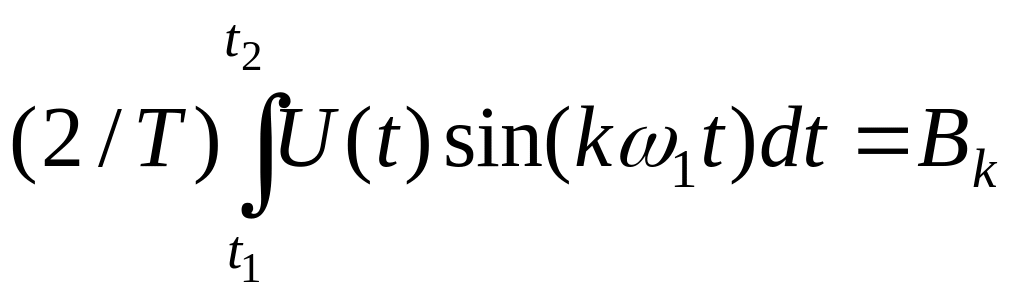Спектр амплитуд
является четной функцией , т. е.
.
.
Спектр
фаз - функция нечетная, т.е.
.
При
получаем
постоянную составляющую:
.
От
двустороннего спектрального представления
можно перейти к одностороннему (не
имеющему отрицательных частот), объединяя
комплексно-сопряженные составляющие
.
В этом случае получаем ряд Фурье в
тригонометрической форме. Выделив в
(1.2.1) постоянную составляющую
с учетом (1.2.2) и обозначив
через
окончательно, получим:
.
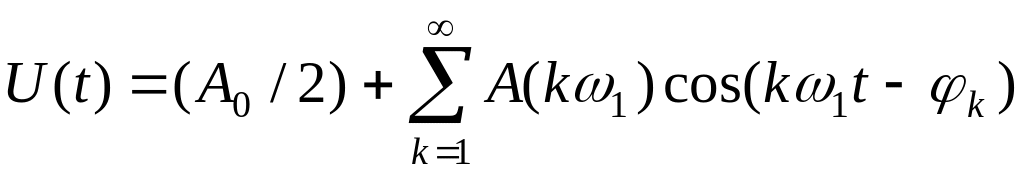Отдельные составляющие и называются гармониками. Как спектр амплитуд, так и спектр фаз периодического сигнала удобно представлять наглядно спектральными диаграммами. На диаграмме спектра амплитуд каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна амплитуде, а расположение на оси абсцисс отвечает частоте этой составляющей. Поскольку в результате спектры отображаются совокупностями линий, они называются линейчатыми.