Контрольные вопросы
1.Что понимают под термином «помехоустойчивость»? Критерии помехо-устойчивости.
2.Частотная модуляция. Ее отличие от фазовой модуляции.
3.Характеристики канала передачи информации.
4.Что такое белый шум? Каковы его характеристики?
5.Как выглядит величина, показывающая, насколько вероятнее появление той или иной реализации в случайном сигнале?
Лабораторная работа № 11
“Пропускная способность непрерывных линейных систем при наличии помех”.
Цель. Исследование влияния отрицательной обратной связи на пропускную способность системы автоматического управления (САУ).
Задание.
Изменяя
параметры САУ, а так же звена обратной
связи получить семейство графиков
функций
,
,
,
.
Зафиксировать пропускную способность
системы автоматического управления
для каждого случая, проанализировать
полученные результаты, сделать выводы.
Отчет по лабораторной работе должен содержать:
- краткие теоретические сведения.
- анализ полученных результатов.
- выводы.
Основные понятия и определения.
1. Пропускная способность.
В системах автоматического управления наиболее существенной информационной характеристикой является пропускная способность каналов, ибо она определяет точность работы всей системы.
Пропускная способность определяется формулой:
,
(11.1.1)
где
- полоса частот сигнала в канале;
– средняя мощность сигнала;
- средняя мощность помехи.
Формула (11.1.1) справедлива для случая, когда канал представляет собой идеальный фильтр, а помеха является нормальным белым шумом.
Опуская теоретические выкладки, скажем, что на случай спектральных плотностей сигнала и помехи произвольной формы, формула примет вид:
,
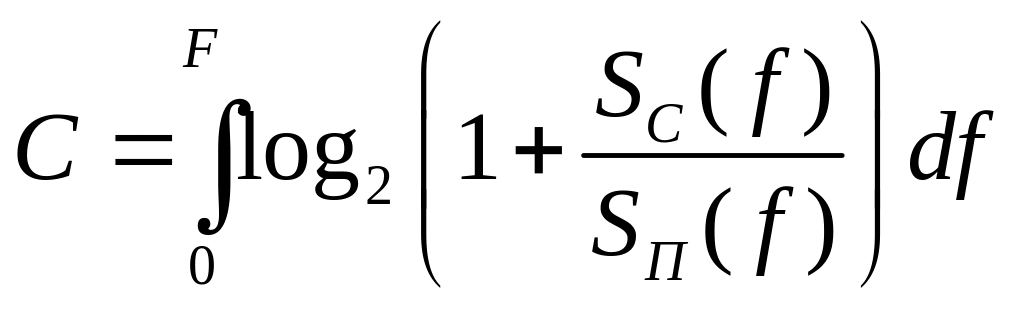(11.1.2)
где
– спектральная плотность сигнала, а
- спектральная плотность помехи.
Чтобы определить пропускную способность любого канала при фиксированном отношении средних мощностей сигнала и помехи, необходимо воспользоваться следующей формулой:
.
(11.1.3)
Для случая белого шума эта формула принимает вид (11.1.1).
2. Линейный “шумящий” фильтр с коэффициентом усиления, изменяющимся случайным образом относительно некоторого постоянного значения.
На
входе фильтра действует стационарный
полезный сигнал
со спектральной плотностью
,
свойства фильтра характеризуются его
импульсной переходной функцией
,
выходной сигнал есть случайная функция
.
Представим
коэффициент усиления в виде суммы двух
составляющих – номинального значения
и случайной компоненты
с равным нулю математическим ожиданием.
Тогда рассматриваемый фильтр будет
состоять из двух параллельно включенных
звеньев – одно из них является фильтром
с постоянными параметрами и импульсной
переходной функцией
.
Здесь
обозначает импульсную переходную
функцию фильтра с единичным коэффициентом
усиления.
Спектральная
плотность помехи
будет определяться выражением:
.
Используя общую формулу для пропускной способности (11.1.2) и учитывая, что спектральная плотность полезного сигнала на выходе фильтра при отсутствии флуктуаций:
,
где
- передаточная функция фильтра с единичным
коэффициентом усиления, получим:
.
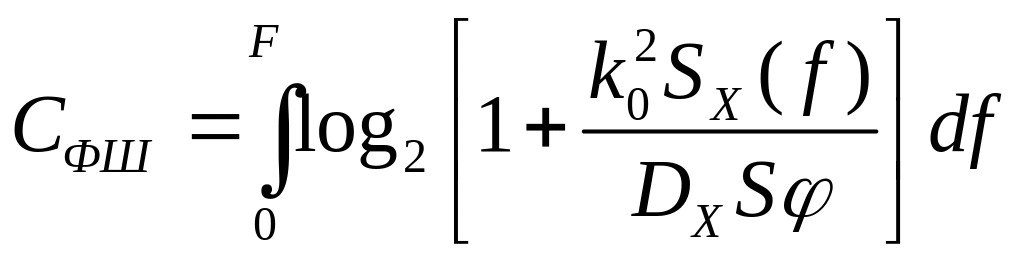(11.2.1)
Без вывода приведём основные формулы, описывающие данную систему автоматического управления:
.
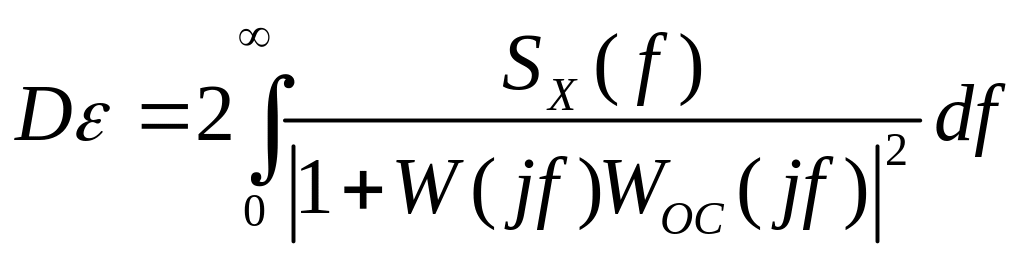(11.2.2)
Данная
формула применяется для расчета дисперсии
сигнала
.
Спектральная плотность помехи на выходе
шумящего звена:
.
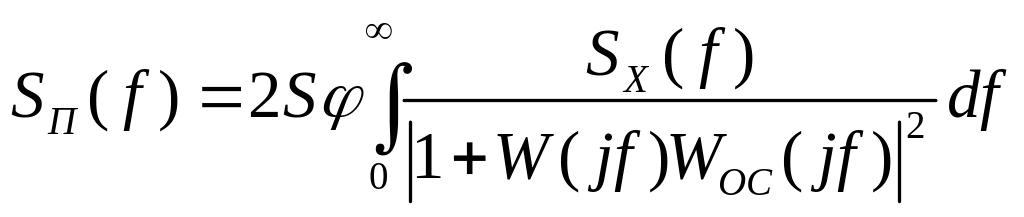(11.2.3)
Мы видим, что охват шумящего звена отрицательной обратной связью уменьшает спектральную плотность помехи на его выходе, так как знаменатель подынтегрального выражения всегда больше единицы.
Однако, спектральная плотность полезного сигнала на выходе упомянутого звена также уменьшается, что не позволяет ожидать существенного увеличения пропускной способности:
.
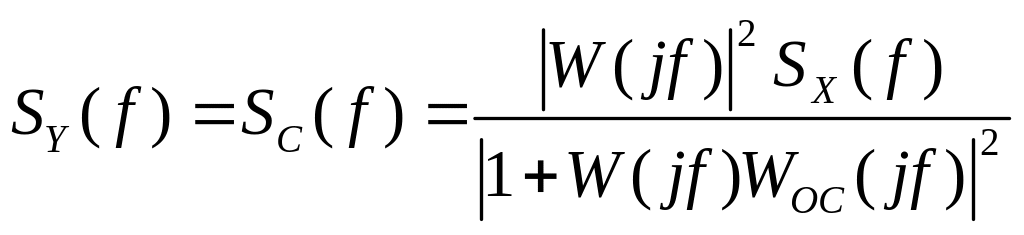(11.2.4)
Подставляя соотношения (11.2.2.) и (11.2.3) в формулу (11.1.2), получим:
.
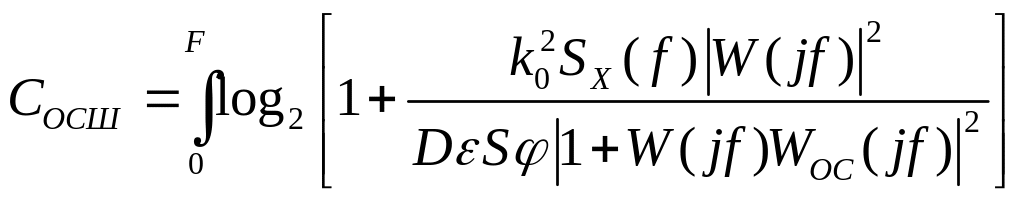(11.2.5)
Сравнение
формул (11.2.5) и (11.2.1) показывает, что они
отличаются значениями дисперсий – при
отсутствии обратной связи используется
дисперсия
,
при наличии обратной связи вместо
появляется квадрат множителя
.
Поскольку последний является частотно-зависимым и убывает с ростом частот, можно ожидать некоторого увеличения пропускной способности звена.