готовые шпоры на 2ой семестр по физике / 12 вопрос

12

Упругое и неупругое соударения

При соударении тел они в большей либо меньшей мере деформируются. При этом кинетическая энергия тел частично или полностью переходит в потенциальную энергию упругой деформации и во внутреннюю энергию тел. Увеличение внутренней энергии приводит к нагреванию тел.

Ограничимся рассмотрением центрального удара двух шаров, при котором шары движутся вдоль прямой, проходящей через их центры. На рис. 1 изображены два возможных случая центрального удара.

Р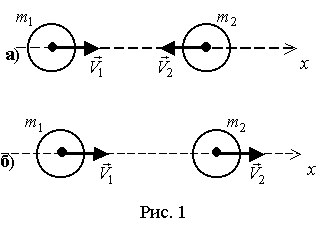ассмотрим два предельных вида соударения - абсолютно неупругий и абсолютно упругий удары.

Абсолютно неупругий удар

Интересным примером, где имеет место потеря механической энергии под действием диссипативных сил, является абсолютно неупругий удар, при котором потенциальная энергия упругой деформации не возникает; кинетическая энергия тел частично или полностью превращается во внутреннюю энергию. После такого удара тела движутся с одинаковыми скоростями (т.е. как одно тело) либо покоятся.

При абсолютно неупругом ударе выполняется только закон сохранения суммарного импульса тел: , откуда,

. (7)

Кинетическая же энергия, которой обладала система до удара, после соударения уменьшается или стремится к нулю. Изменение кинетической энергии:

. (8)

Абсолютно упругий удар

Это такой удар, при котором полная механическая энергия тел сохраняется. Сначала кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела возвращаются к

первоначальной форме, отталкиваясь друг от друга. В итоге потенциальная энергия упругой деформации снова переходит в кинетическую и тела разлетаются со скоростями, которые определяются исходя их законов сохранения суммарного импульса и суммарной энергии тел.

Обозначим массы шаров m₁ и m₂, скорости шаров до удара и , скорости шаров после удара и и напишем уравнения сохранения импульса и энергии:

(9)

Решая совместно эти два уравнения, найдем скорости шаров после абсолютно упругого удара:

(10)

Чтобы осуществить расчеты, нужно спроектировать все векторы на ось х. Сделаем это, например, для случая а) на рис. 1:

. (11)

Если ответ получается положительным, то это означает, что шар после соударения движется вправо, если - отрицательный, то шар движется влево.