Шпора №6

2. Динамика поступательного и вращательного движения

1. Основные формулы

Поступательное движение				Вращательное движение

Дано:

m k

- ?

Масса – m Сила - Импульс - Импульс тела = 2. Импульс силы 3. Импульс системы тел = 1 + 2 + 3 + ... 4. Принцип независимости действия сил Р = 1 + 2 + 3 + ... 5. Второй закон Ньютона = = = 6. Сила гравитационная F = , G = Нм2/кг2 - гравитационная постоянная 7. Сила трения = , k - коэффициент трения

Момент инерции - I Момент силы - Момент импульса - Момент импульса материальной точки относительно точки вращения =;=; = Момент силы относительно точки вращения = ; = = 3. Момент импульса системы тел = + + + ... 4. Результирующий момент силы = + + + ... Основной закон динамики вращательного движения = = = 6. Момент инерции: материальной точки I = , сплошного цилиндра I = , кольца I = , стержня I = , шара I = .

8. Сила упругая = - , k - коэффициент жесткости 9. Вес тела P = 10. Сила тяжести - Ускорение свободного падения

7. Теорема Штейнера I = I0 + , где a - расстояние между произвольной осью вращения и осью вращения, проходящей через центр тяжести тела параллельно заданной оси, I0 – момент инерции тела относительно оси, проходящей через центр тяжести тела.

2.2. Примеры решения задач

Задача 1. Брусок массой m втаскивают за нить с постоянной скоростью вверх по наклонной плоскости, составляющей угол α с горизонтом. Коэффициент трения k. Найти угол β, который должна составлять нить с наклонной плоскостью, чтобы сила натяжения нити была минимальной.

Решение

рис.2.1.

При движении тела вверх с ускорением на него действуют четыре силы – сила тяжести , сила натяжения нити , сила трения и сила реакции опоры . Направления действия этих сил показаны на рис. 2.1. Для решения задачи необходимо выбрать направление осей системы координат. Ось Х направим вдоль поверхности наклонной плоскости в направлении ускорения, а ось Y – перпендикулярно направлению наклонной плоскости. Запишем второй закон Ньютона , (1)

где - равнодействующая всех сил. Спроецируем уравнение (1) на направление осей координат.

Х: (2)

Y: (3)

Сила трения связана с силой реакции опоры соотношением

(4)

Задача сводится к решению системы последних трех уравнений. Из уравнения (3) следует, что

Подставим полученный результат в уравнение (4):

После этого уравнения преобразуем уравнение (2) и учтем, что ускорение тела равно нулю, так как тело движется равномерно.

(5)

Выразим силу натяжения из уравнения (5):

(6)

Сила натяжения будет минимальной, если знаменатель полученного выражения (6) примет максимальное значение. Обозначим через и исследуем эту функцию на экстремум. Для этого возьмем производную от по переменной  и приравняем ее к нулю ().

или . Окончательный ответ:  = arctg k.

Задача 2. Через блок в виде диска, масса которого 100 г, перекинута нить, к концам которой подведены грузы 50 г и 80 г (рис. 2.2).

С каким ускорением будут двигаться грузы, если их

п

редоставить самим себе?

Дано:

m =100 г = 0,1 кг m1 = 50 г = 0,05 кг m2 = 80 г = 0,08 кг g = 9,8

a- ?

Решение

Рис. 2.2.

Применим к решению задачи законы поступательного и вращательного движений. На каждый груз, движущийся поступательно, действуют две силы : сила тяжести, направленная вертикально вниз, и сила натяжения нити, направленная вверх. Решение проводим для каждого тела в отдельности, учитывая, что ускорения тел одинаковы. Ось Y направим по ускорению тел. По второму закону Ньютона уравнения этих тел в проекции на ось Y запишутся следующим образом.

Y:

Силы натяжения нитей действуют не только на грузы, но и на диск. По третьему закону Ньютона силы, приложенные к ободу диска, равны силам Т₁ и Т₂ , приложенным к телам 1 и 2, но противоположно направлены. Под действием этих сил диск вращается против часовой стрелки согласно уравнению

Результирующий вращающий момент сил Т₁ и Т₂

где r - радиус диска.

Момент инерции диска ; угловое ускорение диска  связано с тангенциальным ускорением точек нити соотношением Ускорение тел и тангенциальное ускорение точек нити равны между собой: a = a_.

В итоге мы имеем систему из трех уравнений:

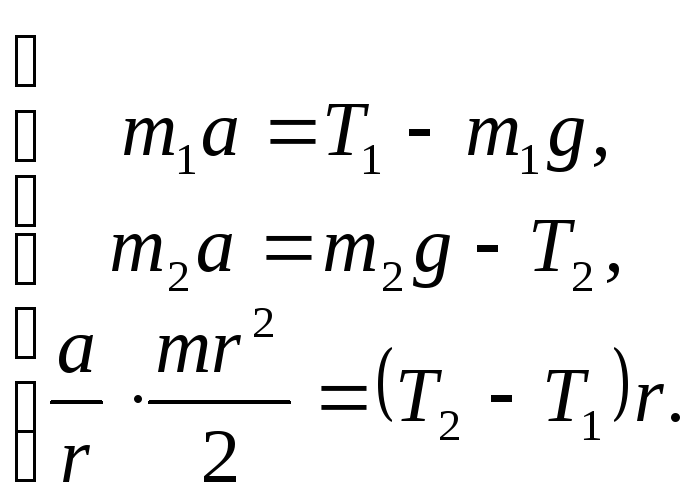
Складывая левые и правые части уравнений, получим

Подставим числовые значения:

Дано:

m1 m2 g

a1- ? a2 - ? T1 - ? Т2 - ?

Задача 3. Определить ускорения, с которыми движутся грузы m₁, m₂ в установке, изображенной на рис. 2.3, а также силы натяжения нитей Т. Трением и массой блоков пренебречь. Нить считать невесомой и нерастяжимой.

Р

ешение

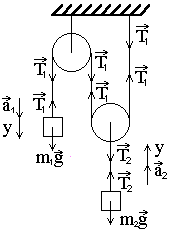
Рис. 2. 3

На груз m₁ действует сила тяжести и сила натяжения нити Т₁, на груз m₂ - сила тяжести и сила натяжения Т₂ . Запишем для каждого тела в отдельности второй закон Ньютона в скалярном виде, выбрав направление оси Y по направлениям ускорений тел, считая, что ускорение груза m₁ направлено вниз, а груза m₂ - вверх.

, (1)

. (2)

Условия, связывающие модули ускорений грузов a₁ и a₂, можно получить, учитывая: а) условие не растяжимости нити: Т₂ = 2Т₁ (блоки не вращаются); б) соотношение между модулями перемещений грузов, происходящих за одно и то же время : S₁ = 2S₂. Очевидно, такое же соотношение существует и между модулями ускорений грузов (S = a t²/2):

a₁ = 2a₂. (3)

Решая совместно уравнения (1) - (3), получаем

Т₂ = 2Т₁; a₂ = a₁/2.

Задача 4. Два шара массой m и 2m ( m = 10 г ) закреплены на тонком, невесомом стержне длиной 40 см так, как показано на рис. 2.5. Определить момент инерции I системы относительно оси, перпендикулярной к стержню и проходящей через его конец. Размерами шаров пренебречь.

Дано:

m1 = m m2 = 2m m = 10 г = 10-2 кг = 40 см = 0,4 м

I - ?

Решение

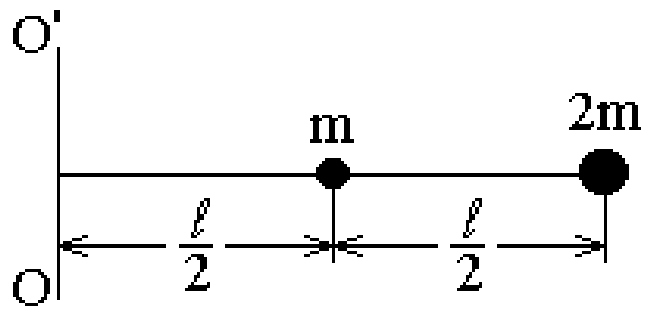
Рис. 2.5

Момент инерции системы I равен алгебраической сумме моментов инерции тел, входящих в систему:

I = I₁ + I₂,

где I₁ - момент инерции 1-го шара относительно оси ОО^, I₂ - момент инерции 2-го шара относительно той же оси (рис. 2.5). Считаем шары материальными точками Тогда

Таким образом,

I = 2,2510^-20,4² = 3,610^-3 кгм².

Дано:

m = 50 кг r = 20 см = 0,2 м n0 = 480 об/мин = 8 об/с с

M - ?

Задача 5. Сплошной шар массой 1 кг и радиусом 0,05 м вращается вокруг оси, проходящей через его центр. В точке, наиболее удаленной от оси вращения, на шар действует сила, касательная к поверхности. Угол поворота шара меняется по закону Определить величину действующей силы, тормозящий момент, время равнозамедленного движения.

Дано:

m = 1 кг R = 0,05 м

F - ? M - ? t - ?

Решение

1. Вращение шара происходит по закону динамики вращательного движения

,

где M - тормозящий момент, I - момент инерции шара и - угловое ускорение, которое определим как вторую производную от углового перемещения  по времени (). Тормозящий момент

Нм.

2. Момент силы есть произведение силы на ее плечо а тогда

Н.

3. Время движения определим из уравнения для угловой скорости равнозамедленного движения ,

Так как тело останавливается, то конечная угловая скорость  равна нулю.

где - начальная скорость. Угловая скорость есть первая производная от угла поворота по времени:

Из последнего выражения при t = 0 имеем рад/с.

Таким образом, с.

Задача 6. Маховик в виде диска массой 50 кг и радиусом 20 см был раскручен до частоты 480 об/мин и затем предоставлен самому себе. Под влиянием трения маховик остановился. Найти момент M сил трения, считая его постоянным, если маховик остановился через с.

Решение

По закону динамики вращательного движения имеем . Изменение момента импульса

L = L₂ - L₁ = I - I₀,

где I - момент инерции маховика, , - начальная угловая скорость,  = 0 - конечная угловая скорость. Тогда

,

Нм.

Знак минус показывает, что момент силы трения оказывает тормозящее действие.

Задача 7. Гиря массой 200 г вращается на невесомом нерастяжимом стержне в вертикальной плоскости. Насколько сила натяжения стержня больше при прохождении гири через нижнюю точку, чем через верхнюю?

Дано:

m = 0,2 кг

T - ?

Решение

Решение задачи проводим отдельно для верхней и нижней точек окружности (рис. 2.6).

В верхней точке на гирю действуют сила тяжести и сила натяжения нити . Проведем ось Y по направлению центростремительного ускорения, т.е. к центру окружности. Запишем векторное уравнение второго закона Ньютона: .

Проецируя силы на ось Y и используя формулу , получим уравнение , из которого определим силу натяжения стержня Т₁:. (1)

В нижней точке на гирю действуют: сила тяжести и сила натяжения нити . Проведем ось Y вверх по направлению центростремительного ускорения. Запишем скалярное уравнение второго закона Ньютона в проекции на ось Y:

,

из которого определим силу натяжения стержня Т₂ .

. (2)

Из (1) и (2) получим:

,

Н.

рис. 2.7

Задача 8. Груз массой 0,1 кг, подвешенный к шнуру длиной 1 м, движется равномерно по окружности в горизонтальной плоскости так, что шнур описывает коническую поверхность и отклоняется от вертикали на угол 60⁰. Определить период вращения груза по окружности (рис. 2.7).

Дано:

m = 0,1 кг = 1 м

T - ?

Решение

На груз действуют: сила тяжести и сила натяжения нити . Проведем ось X горизонтально по направлению центростремительного ускорения.

Запишем уравнение второго закона Ньютона в векторной форме:

Заметим, что равнодействующую силу F_Р по величине можно найти как катет треугольника MBN.

Тогда . (1)

Радиус окружности R определим из  ABC:

(2)

Скорость перемещения V получим с учетом (2):