Шпора №7

Работа при перемещении пров. с током в магн. поле.

На элемент проводника с током в магн. поле действует сила Ампера:

Если при этом проводник перемещ. на , то сила Ампера соверш. элементарную работу:

- магн. поток сквозь малую площадку прочерч. эл. при его малом перемещении .

При перемещении в том же поле пров. конечной длины сила Ампера соверш. работу:

- магн. поток сквозь поверхность прочерч. пров. конечной длины при бесконечно малом перемещ .

При перемещении всего проводника из положения 1 в положение 2 работа силы Ампера составит:

Рассм. замкн. контур с пост. током перемещ. в магн. поле.

Работа сил поля при бесконечно малом перемещ. контура выраж. формулой:

где -магн. поток сквозь поверхн. прочерченую всем контуром при его малом перемещ. .

Этот магн. поток можно выразить через потокосцепление контура в нач. и конечном положениях.

Поверхности неатянутые контуром в нач. и конечном полож. совместно с поверхн. прочерч. контуром образуют замкн. поверхность к которой можно применить теорему Гауса-Ост.:

Интегрируя получим:

Работа сил Ампера при перемещ. в пост. магн. поле замкн. проводника с пост. током равна произв. силы тока в контуре на изменение его потокосцепления.

Теорема Гауса-Остр. для магн. поля.

Магн. потоком сквозь малую поверхность назыв. скал. величина равная:

Малая площадка выбир. так, чтоб её можно было считать плоской, а поле в её пределах однородным.

Магн. поток сквозь произв. поверхность:

Для плоской поверхн. в однор. магн. поле:

Теорема Гауса-Остроградского для магн. поля

Магн. поток сквозь произв. замкнутую поверхностьравен нулю:

Магн. поток сквозь поверхн. ограниченую замкнутым контуром назыв.- потокосцеплением этого тока.

Для катушки из n-витков потокосцепл. равно:

;

Потокосцепление взаимной индукции 2-х контуров – это потокосцепление одного из них обусл. магн. полем тока во втором контуре.

Первое уравнение Максвела явл. обобщением закона эл. магн. индкуции:

Появление ЭДС инд. В неподв. контуре находящемся в переменном магн. поле может быть

обьснено только тем, что переменное магн. поле вызыв. появление непотенциального эл. поля, под действием которого и возникает инд. ток.

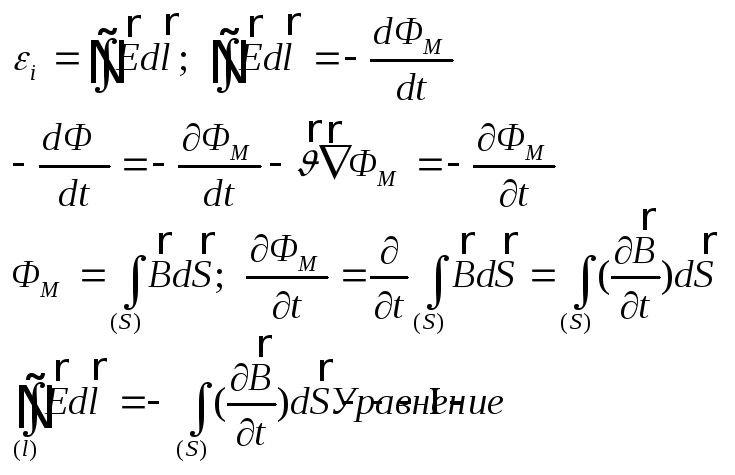
Переменное магн. поле порождает в окруж. пространстве вихревое эл.поле для которого цирк. вектора

Если в этой области простр. имеется проводящий замкнутый контур то в нём возникает инд. ток B

В дифференциальной форме:

Преобразуем первую часть с помощюь теоремы Стокса:

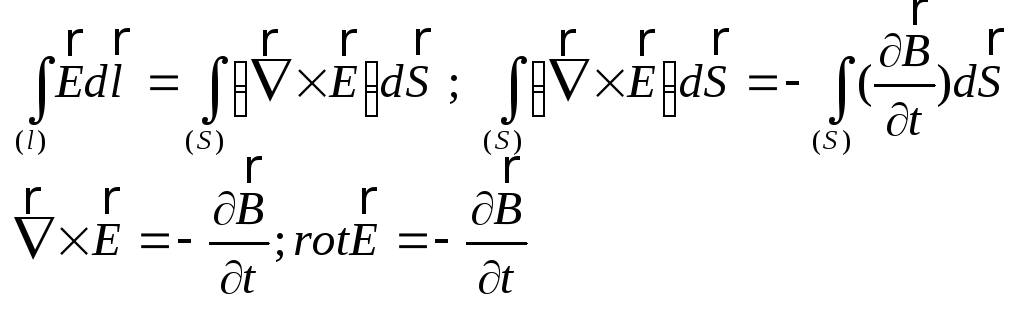
Свободные эл. магн. колебания в электр. колебательном контуре.

Простейший колебательный контур состоит из послед. соединений конденсатора, катушки и резистора.

Если конденсатор предвар. заряжён, то при замыкании в цепи в ней возникает переменный эл. ток.

Из закона Ома следует:

После подстановки получаем:

Если сопротивление контура мало, то это выражение превращ. в дифференц. уравн. гармонич. колебаний.

Отсюда следует, что заряд на обкладках конденсатора и сила тока с контуре меняется по гармон. закону.

Меняется по гармон. закону инфазно с зарядом.

Амплитудные значения тока и разности потенц. связаны между собой соотношениями:

;-волн. сопрот. контура.

При свободном колебании контура происходит преобр. эл. поля конденсатора в магн. поля катушки и обратно.

Атом в магн. поле

Классическая физика считает что, каждый электрон в атоме движеться по плоской круговой орбите пост. радиуса, образуя замкнутый орбитальный ток.

Сила орбит. тока:

Орбитальному току соответствует дрб магн. момент электрона.

Электрон обладает моментом импульса относительно центра орбиты точки О – орбитальным моментом импульса

Векторы -перепендик. плоскости орбиты и направл. вдоль одной прямой в противоположные стороны.

Можно записать:

Орбитальные моменты атома опред. как суммы соответств. орбит моментов электронов.

z – число электр. в атоме совпад. с числом протонов в его ядре, из с порядковым № в элемента в период. сист. Менделеева.

Очевидно:

Для атома с оболочкой сост. Из Z электронов: