3.10 Теорема о структуре общего решения неоднородного ду

Теорема. Общее решение линейного неоднородного дифференциального уравнения

в некоторой области есть сумма любого его решения и общего решения соответствующего линейного однородного дифференциального уравнения.

Доказательство. Пусть Y – некоторое решение неоднородного уравнения. Тогда при подстановке этого решения в исходное уравнение получаем тождество:

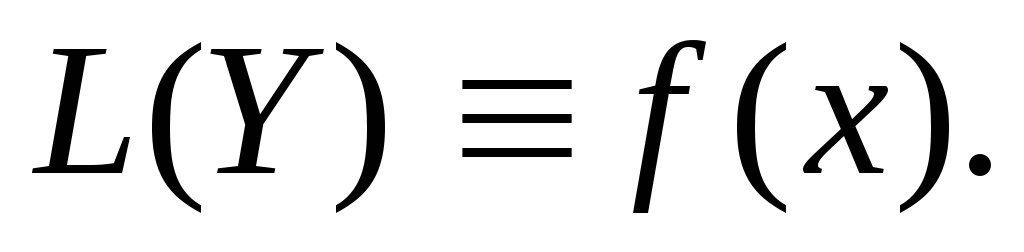Пусть - фундаментальная система решений линейного однородного уравнения. Тогда общее решение однородного уравнения можно записать в виде:

Далее покажем, что сумма является общим решением неоднородного уравнения.

Вообще говоря, решение Y может быть получено из общего решения, т.к. является частным решением.

Таким образом, в соответствии с доказанной теоремой, для решения линейного неоднородного дифференциального уравнения необходимо найти общее решение соответствующего однородного уравнения и каким- то образом отыскать одно частное решение неоднородного уравнения. Обычно оно находится подбором.