3.4 Уравнение в полных дифференциалах и их решение

Пусть задано диф. ур-е ел. Вида:гдеP(x,y) и Q(x,y) – непрер. Функции имеющие непрерыв часн. Производную 2 порядка включительно. Диф. ур. Назыв. Ур-ем в полных диф-лах , если такое что

т.е. ур. В этом случае имеет вид :

это уравнение явл полным диф. функции U как ф-ции двух переменных:

сли выполняется равенство тогда то левая часть а тогда его решение

- общий интеграл диф. Ур.

Теорема о необходимости и достаточности условия того что Ур было ур-ем в полных дифференциалах

Теорема : Для того чтобы ур было ур-ем в полных диф. в некоторой Д принадл ХОУ

Необх. И дост. Чтобы во всех точках обл. Д выполн равенство если условие выполняется можно найти ф-циючто будет выполняться рав-во след. Образом.

найдем

3.1 Обыкновенные дифференциальные уравнения называется уравнение, связывающее независимые переменные, их функции и производные (или дифференциалы) этой функции. Определение. Если дифференциальное уравнение имеет одну независимую переменную, то оно называется обыкновенным дифференциальным уравнением, если же независимых переменных две или более, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.

Наивысший порядок производных, входящих в уравнение, называется порядком дифференциального уравнения. Пример. - обыкновенное дифференциальное уравнение 1 – го порядка. В общем виде записывается.

- обыкновенное дифференциальное уравнение 2 – го порядка. В общем виде записывается

- дифференциальное уравнение в частных производных первого порядка. Определение. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество.

Дифференциальным уравнением первого порядка называется соотношение, связывающее функцию, ее первую производную и независимую переменную, т.е. соотношение вида: Если такое соотношение преобразовать к виду то это дифференциальное уравнение первого порядка будет называться уравнением,разрешенным относительно производной. Преобразуем такое выражение далее:

Функцию f(x,y) представим в виде: тогда при подстановке в полученное выше уравнение имеем:

это так называемая дифференциальная форма уравнения первого порядка. Общим решением дифференциального уравнения называется такая дифференцируемая функция y = (x, C), которая при подстановке в исходное уравнение вместо неизвестной функции обращает уравнение в тождество. Решение вида у = (х, С₀) называется частным решением дифференциального уравнения. (теорема о существовании и единственности решения дифференциального уравнения 1- го порядка) Если функция f(x, y) непрерывна в некоторой области D в плоскости XOY и имеет в этой области непрерывную частную производную , то какова бы не была точка (х₀, у₀) в области D, существует единственное решение уравнения, определенное в некотором интервале, содержащем точку х₀, принимающее при х = х₀ значение (х₀) = у₀, т.е. существует единственное решение дифференциального уравнения Особым решением дифференциального уравнения называется такое решение, во всех точках которого условие единственности Коши не выполняется, т.е. в окрестности некоторой точки (х, у) существует не менее двух интегральных кривых. Особые решения не зависят от постоянной С. Особые решения нельзя получить из общего решения ни при каких значениях постоянной С. Если построить семейство интегральных кривых дифференциального уравнения, то особое решение будет изображаться линией, которая в каждой своей точке касается по крайней мере одной интегральной кривой.

Отметим, что не каждое дифференциальное уравнение имеет особые решения.

3.3 Линейные ДУ 1-порядка (методом вариаций).

Метод подстановки. Линейным уравнением 1-го порядка называют уравнения вида: y’+yP(x)=Q(x) – гдеP(x) иQ(x) некоторые функции переменной х , аy’ иyвходят в уравнение в 1 степени.

1.Метод подстановки:

Будем искать решение уравнения 1 в виде

произведения y=U(x)V(x) при чём так, что мы

можем подобрать одну из функций по желанию,

а вторую так, чтобы удовлетворяла (1) :

y’=U’V+UV’ ; U’V+UV’+UV*P(x)=Q(x) ;

U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x)

y’+y cos(x)=1/2 sin(2x) y=UV

U’V+UV’+UVcos(x)=sin(x)cos(x)

V’+Vcos(x)=0 dV/V=-cos(x)dx

ln(V)= -sin(x) V=e^-sin(x)

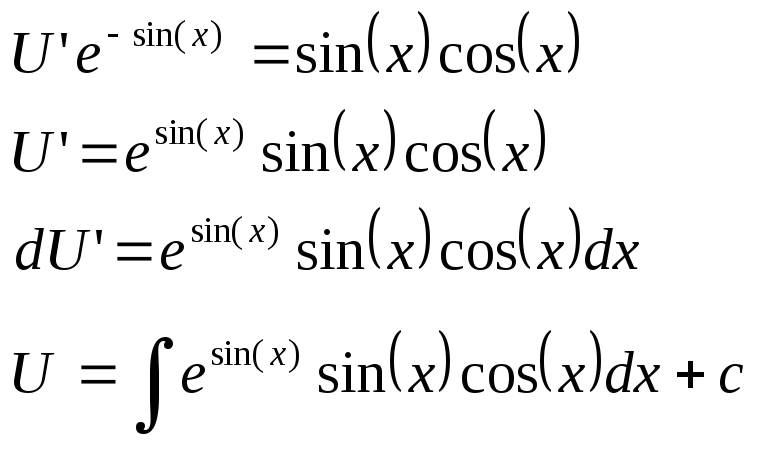
sin(x)=t

Метод вариации производной постоянной при решении линейного диф. уравнения 1-го порядка.

y’+P(x)y=Q(x) (1) -задано линейное неоднородное уравнение. Рассмотрим соотв. ему однородное уравнение y’=P(x)y=0 (2). Найдём общее решение:

Будем искать решение в том же виде, что и однородного, только считая с не произвольной константой ,а функцией от х :