
MatAnal
.docxЧто называется градиентом функции?
Градиентом функции u=f(x, y, z) в точке M(x, y, z), называется вектор, координатами которого служит значение частных производных этой функции заданных в точке М.
grad
u =
 =
=

Что называется максимумом, минимумом, экстремумом функции двух переменных?
(x0, y0) – точка максимума функции z = f(x, y), если существует -окрестность этой точки, для всех точек которой выполняется неравенство f(x0, y0) > f(x, y);
(x0, y0) – точка минимума функции z = f(x, y), если существует -окрестность этой точки, для всех точек которой выполняется неравенство f(x0, y0) < f(x, y).
Как с помощью двойного интеграла вычислить площадь плоской области D?
Двойной
интеграл 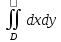 численно
равен площади плоской фигуры D (области
интегрирования). Это простейший вид
двойного интеграла, когда функция двух
переменных равна единице: f
(x,
y)
= 1.
численно
равен площади плоской фигуры D (области
интегрирования). Это простейший вид
двойного интеграла, когда функция двух
переменных равна единице: f
(x,
y)
= 1.
Сначала
рассмотрим задачу в общем виде. Сейчас
вы немало удивитесь, насколько всё
действительно просто! Вычислим площадь
плоской фигуры ![]() ,
ограниченной линиями x
= a,
x=
b,
y
= f(x),
y
= g(x).
Для определённости считаем, что f(x)
> g(x) на
отрезке [a,
b].
Площадь данной фигуры численно равна:
S
=
,
ограниченной линиями x
= a,
x=
b,
y
= f(x),
y
= g(x).
Для определённости считаем, что f(x)
> g(x) на
отрезке [a,
b].
Площадь данной фигуры численно равна:
S
=

Изобразим
область D на
чертеже:

Выберем первый способ обхода области: g(x)<=y<=f(x), a<=x<=b
Таким
образом:
S
=
 =
=
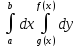
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую начинающим в теме чайникам.
1)
Вычислим внутренний интеграл, при этом
интегрирование проводится по переменной
«игрек»:
 = f(x)
– g(x)
= f(x)
– g(x)
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, в функции. Сначала подставили в «игрек» (первообразную функцию) верхний предел, затем – нижний предел
2) Результат, полученный в первом пункте необходимо подставить во внешний интеграл:

Более
компактная запись всего решения выглядит
так:

S
=
 =
=
 =
= =
=

Что называется тройным интегралом от функции u =f (х, у, z) по пространственной области V?
Тройным интегралом от функции f(x, y, z) по области V называется конечный предел трехмерной интегральной суммы при стремлении к нулю ранга разбиения, порождающего эту сумму (если этот предел существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек на каждой из этих элементарных частей):
![]()
здесь n – это количество элементарных частей разбиения области V; Pi (xi,yi,zi) – произвольно выбранная точка на каждой элементарной части,
i = 1,...,n;
![]() —
ранг
разбиения;
—
ранг
разбиения;
![]() – диаметр i-ой
элементарной части.
– диаметр i-ой
элементарной части.
Сколько фундаментальных систем решений имеет такое ДУ? Почему?
Какова структура общего решения линейного однородного ДУ n-го порядка?
Рассмотрим на [a; b] линейное однородное дифференциальное уравнение
y(n) + an-1(x)y(n - 1) + ... + a1(x)y' + a0(x)y = 0.
Общим решением этого уравнения на отрезке [a;b] называется функция y = Φ(x, C1,..., Cn ), зависящая от n произвольных постоянных C1,..., Cn и удовлетворяющая следующим условиям :
− при любых допустимых значениях постоянных C1,..., Cn функция y = Φ(x, C1,..., Cn ) является решением уравнения на [a; b] ;
− какова бы ни была начальная точка (x0, y0, y1,0 ,..., yn − 1,0 ) , x0∈ [a;b] , существуют такие значения C1 =C10 , ..., Cn = Cn0 , что функция y = Φ(x, C10 , ..., Cn0) удовлетворяет начальным условиям y(x0) = y0, y '(x0) = y1,0 ,..., y(n − 1) (x0) = yn− 1,0 .
Справедливо следующее утверждение ( теорема о структуре общего решения линейного однородного уравнения).
Если все коэффициенты уравнения линейного однородного дифференциального уравнения непрерывны на отрезке [a;b] , а функции y1(x), y2(x),..., yn(x) образуют фундаментальную систему решений этого уравнения, то общее решение уравнения имеет вид
y(x,C1,..., Cn) = C1 y1(x) + C2 y2(x) + ... + Cn yn(x),
где C1,...,Cn — произвольные постоянные.
Каково необходимое и достаточное условие разложимости функции в ряд Тейлора?
Для того чтобы f(x) могла быть разложена в степенной ряд, необходимо и достаточно, чтобы она в интервале сходимости имела производные всех порядков, и чтобы остаточный член формулы Тейлора -> 0, и n -> бесконечности.
Необходимость
Дано: функция разложена в степ. ряд;
Док-ть: что она дифференцируема бесконечное число раз и предел Rn (x) = 0, при n -> бесконечности.
Док-во: все производные существуют, т. к. функция разложена в ряд. limn->∞ Rn(x) = limn->0 (f(x)-Sn(x)) = f(x)-f(x) = 0
Достаточность
Дано: функция дифференцируема бесконечное число раз и предел Rn (x) = 0, при n -> бесконечности;
Док-ть: функция разложена в степ. ряд.
Док-во: т. к. функция дифференцируема бесконечное число раз, то можно записать Sn(x) = f(0) + f’(0)/1! * x + … + f(n)(0)/n! * xn
