§ 3. Уравнения с разделяющимися переменными

Дифференциальное уравнение называетсяуравнением с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде . Тогда, в случае, общим решением уравнения является.

§ 4. Однородные дифференциальные уравнения 1-го порядка.

Определение 1. Уравнение 1-го порядка 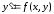называется однородным, если для его правой части при любых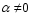справедливо соотношение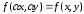, называемое условием однородности функции двух переменных нулевого измерения.

§ 7. Линейные дифференциальные уравнения 1-го порядка.

Линейным уравнением 1-го порядка называется уравнение, линейное относительно искомой функции и ее производной. Оно имеет вид:

, (7.1)

где P(x) и Q(x) – заданные непрерывные функции от x. Если функция ,то уравнение (7.1) имеет вид: (7.2)

и называется линейным однородным уравнением, в противном случае оно называется линейным неоднородным уравнением.

Линейное однородное дифференциальное уравнение (7.2) является уравнением с разделяющимися переменными:

(7.3)

§ 8. Уравнение Бернулли.

Определение.

Дифференциальное уравнение вида , где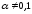, называется уравнением Бернулли.

§ 9. Дифференциальные уравнения в полных дифференциалах.

Определение. Если в уравнении M(x,y)dx+N(x,y)dy=0 (9.1) левая часть есть полный дифференциал некоторой функции U(x,y), то оно называется уравнением в полных дифференциалах.

Сформулировать теорему Коши для ДУ n-го порядка?

Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка

Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y(x) системы Y' = F(x,Y), что Y(x0)=Y0, где Y0 — некоторый постоянный вектор.

 

Справедлива следующая теорема о существовании и единственности решения задачи Коши.

Теорема Коши. Пусть в области D из Rn+1 непрерывны все компоненты вектора правой части F(x,Y) и их частные производные по Y:

 

Тогда, какова бы ни была начальная точка (x0,Y0) ≡ (x0,y1, 0 ,y2, 0, … ,yn, 0 ) ∈ D , существует такой отрезок [x0 − h; x0 + h] , что задача Коши   Y' = F(x,Y), что Y(x0)=Y0 имеет единственное решение.

 

Важно понимать, что теорема Коши имеет локальный характер: существование решения Y = Y(x) гарантируется лишь в достаточно малой окрестности точки x0 , ( h > 0 может оказаться достаточно малым).

 

Важно также понимать, что теорема содержит только достаточные условия существования и единственности решения — при нарушении условий теоремы задача Коши может иметь или не иметь решений, может иметь несколько решений.

Как ставится задача Коши для ДУ n-го порядка?

Что называется общим решением ДУ n-го порядка?

При каких р>0 сходятся несобственные интегралы ,?

Итак, по определению, 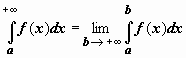. Если этот предел существует и конечен, интегралназывается сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся.

Неопределённый и определённый интеграл функции одной переменной.

Совокупность F(x)+C всех первообразных функции f(x) на множестве Х называется неопределенным интегралом и обозначается: