3. Кинетостатика плоского рычажного механизма

2-ГО КЛАССА

Основной задачей кинетостатического (силового) анализа механизмов является определение реакций в кинематических парах. Значение этих сил необходимо при расчете звеньев механизма на прочность, жесткость, виброустойчивость, износостойкость, при расчете подшипников на долговечность и проведении других подобных расчетов, выполняемых при проектировании механизмов.

Дополнительная задача динамического анализа механизмов состоит в определении уравновешивающей силы или уравновешивающего момента, приложенных к кривошипу. Эти силовые факторы являются функциями положения кривошипа и в данный момент обеспечивают его состояние покоя или равномерного вращательного движения

Кинетостатический расчет механизмов основан на использовании принципа Даламбера: если в каждый момент времени к активным силам, действующим на звенья работающего механизма, и силам реакций связей прибавить силы инерции звеньев, то механизм можно рассматривать, как находящийся в равновесии, а неизвестные силы при этом можно определять теми же методами, что и при статическом расчете механизмов.

Кинетостатический расчет механизмов ведется по структурным группам, так как они обладают нулевой подвижностью и, следовательно, являются статически определимыми системами. Кинетостатический расчет начинается с расчета структурной группы, в которую входит самое удаленное ведомое звено механизма, и завершается расчетом ведущего звена – кривошипа.

При выполнении кинетостатического расчета механизма должен быть задан закон движения ведущего звена и проведен полный кинематический анализ. Кроме того, должны быть заданы все внешние силы, действующие на механизм, например, силы «полезного» (производственного) сопротивления. К данным силам также относятся силы тяжести звеньев, которые определяются формулой:

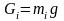, (3.1)

где 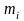– масса i-го звена, (кг);

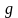– ускорение свободного падения, (м/с²).

В современных быстроходных машинах отдельные звенья механизма, обладая значительными массами, движутся с большими ускорениями. Это приводит к появлению инерционных (динамических) нагрузок на звенья и кинематические пары, во много раз превышающих статические нагрузки.

Поэтому одной из важнейших задач кинетостатического анализа является учет сил инерции и моментов сил инерции звеньев. Инерционные нагрузки зависят от характера движения звена и определяются с использованием результатов кинематического анализа механизма.

1. Определение инерциальной нагрузки звеньев механизма

Из теоретической механики известно, что все силы инерции звена, совершающего плоскопараллельное движение и имеющего плоскость симметрии, параллельную плоскости движения, могут быть сведены к силе инерции , приложенной в центре масс S звена, и к паре сил инерции, момент которой равен .

Величина силы инерции определяется по формуле:

, (3.2)

где 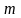– масса звена, (кг);

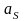– ускорение центра масс S звена, (м/с²).

Сила инерции имеет размерность [Н], [кН]. Направление силы инерции противоположно направлению вектора ускорения центра масс звена.

Момент сил инерции направлен противоположно угловому ускорению 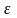и его величина определяется по формуле:

(3.3)

где 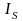– момент инерции звена относительно оси, проходящей через центр масс S звена и перпендикулярной к плоскости движения звена, ( );

– угловое ускорение звена, (с^-2).

Моменты инерции стержневых звеньев относительно оси, проходящей через центр масс S будем определять по формуле:

, (3.4)

где – масса звена;

– длина звена.

Рассмотрим несколько примеров определения сил инерции звеньев, совершающих различные движения.

1. Звено совершает поступательное движение. На рис. 3.1. поршень 1 (ползун) массой 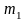движется в цилиндре с некоторым ускорением . В этом случае сила инерции поршня направлена противоположно ускорению поршня и определяется по формуле: .

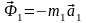Рис. 3.1. Схема к определению силы инерции поступательно движущегося звена

2. Звено совершает вращательное движение. На рис. 3.2. звено 1 массой совершает вращательное движение вокруг оси О с некоторым угловым ускорением . Центр масс S звена не совпадает с осью вращения.

Рис. 3.2. Схема к определению силы инерции вращающегося звена

Сила инерции звена определяется по формуле:

,

в которой ускорение центра масс S звена 1 выражается формулой:

,

где 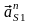– нормальное ускорение центра масс S звена 1, направленное по звену к центру вращения О, и определяемое по формуле: ;

– тангенциальное ускорение центра масс S звена 1, направленное перпендикулярно звену 1 в сторону вращения углового ускорения , и определяемое по формуле: .

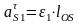Направление ускорения центра масс S звена 1 определяется сложением векторов и , а его величина

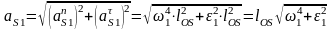. (3.4)

Направление силы инерции звена 1 противоположно вектору ускорения 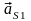. Величина момента сил инерции определяется формулой:

.

Направление момента сил инерции звена 1 противоположно направлению углового ускорения .

3. Звено совершает плоскопараллельное движение. Рассмотрим шатун АВ, который совершает плоскопараллельное движение (рис. 3.3а). Для этого звена в общем виде в масштабе построен план ускорений (рис. 3.3б).

Рис. 3.3 Схема к определению сил инерции звена, совершающего

плоскопараллельное движение:

а) кинематическая схема звена; б) план ускорений

Сила инерции звена определяется по формуле:

.

Ускорение центра масс определим из плана ускорений:

.

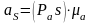Перенесем в точку S звена АВ вектор ускорения центра масс и в противоположную сторону направим вектор силы инерции звена (рис. 3.3а).

Момент силы инерции звена АВ определяем по формуле:

.

Угловое ускорение звена АВ определим по формуле:

.

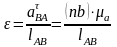С помощью вектора определим направление углового ускорения звена АВ. Перенесем в точку В звена АВ вектор ускорения (рис. 3.3а). По направлению вектора ускорения видно, что угловое ускорение вращается против хода движения часовой стрелки. Следовательно, направление момента сил инерции звена 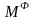будет по часовой стрелке.

Пример №5. Для заданного механизма (рис. 2.5а) определить инерционную нагрузку звеньев кривошипно-ползунного механизма. План ускорений и значения ускорений точек и звеньев механизма для заданного положения механизма взять из примера №4.

Дано: , , , , , , .

Решение: Определим инерционную нагрузку всех звеньев механизма. Сила инерции шатуна 2 равна:

.

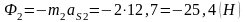Направление силы инерции шатуна 2 противоположно направлению ускорения центра масс , взятого из плана ускорений (рис. 3.4а).

Сила инерции ползуна 3 равна:

.

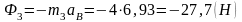Направление силы инерции ползуна 3 противоположно направлению ускорения ползуна В – , взятого из плана ускорений (рис. 3.4а).

Момент силы инерции шатуна 2 определяем по формуле:

.

С помощью вектора , взятого из плана ускорений, определим направление углового ускорения звена АВ. Перенесем в точку В звена АВ вектор ускорения (рис. 3.4а). По направлению вектора ускорения видно, что угловое ускорение вращается по ходу движения часовой стрелки. Следовательно, направление момента сил инерции звена будет против хода часовой стрелки (рис. 3.4а).

Рис. 3.4. Схема к определению инерционной нагрузки звеньев

кривошипно-ползунного механизма:

а) кинематическая схема механизма; б) план ускорений