2. Кинематические цепи

Кинематической цепью называется совокупность звеньев, соединенных в кинематические пары. Кинематические цепи подразделяются на простые, сложные, замкнутые, незамкнутые.

Простой кинематической цепью называется такая цепь, у которой каждое звено входит не более чем в две кинематические пары (рис. 1.3). Например, кривошипно-шатунный механизм состоит из неподвижного звена – стойки и трех подвижных звеньев – 1, 2, 3. Кинематическими парами данного механизма будут 0-1, 1-2, 2-3, 3-0. Каждое звено механизма входит в две кинематические пары, следовательно – это простая кинематическая цепь.

Рис. 1.3. Кинематическая схема кривошипно-шатунного механизма

Сложной называется такая кинематическая цепь, у которой хотя бы одно звено входит более чем в две кинематические пары. В механизме, изображенном на рис. 1.1, звено 2 входит в следующие кинематические пары: 1-2, 2-3, 2-4.

Замкнутой кинематической цепью называется цепь, каждое звено которой входит, по крайней мере, в две кинематические пары (рис. 1.1, 1.3).

Незамкнутой называется кинематическая цепь, у которой есть звенья, входящие только в одну кинематическую пару. На рис. 1.4 звено 5 входит только в одну кинематическую пару: 4-5.

Рис. 1.4. Кинематическая схема манипулятора

Кинематическая схема механизма дает полное представление о структуре механизма и определяет его кинематические свойства. Она выполняется графическим способом с использованием условных обозначений звеньев, кинематических пар и указанием размеров, которые необходимы для кинематического анализа механизма.

На кинематических схемах механизмов звенья изображаются отрезками прямых и нумеруются арабскими цифрами. Кинематические пары обозначаются заглавными буквами латинского алфавита и схематически изображаются так, как показано на рис. 1.3, 1.4.

Для проектируемого механизма необходимо знать какое количество звеньев, связанных со стойкой, должно быть ведущим для того, чтобы движение механизма было вполне определенным. Для этого вычисляют число степеней свободы W механизма относительно стойки, которое показывает количество ведущих звеньев. Большинство механизмов, используемых в технике, имеют число степеней свободы, равное единице и, следовательно, должны иметь одно ведущее звено.

3. Определение класса плоских механизмов

Кроме классификации механизмов на плоские и пространственные предлагается делить их на классы согласно принципу структурного образования механизмов, сформулированному в 1914 году русскими учеными Л.В. Ассуром и И.И. Артоболевским. В соответствии с данным принципом, схема любого механизма может быть составлена последовательным присоединением к ведущему звену (или ведущим звеньям) и стойке кинематических цепей с числом степеней свободы равным нулю, т.е. W = 0. Такие кинематические цепи называют структурными группами или группами Ассура. Группа Ассура – это кинематическая цепь с нулевой степенью свободы относительно тех звеньев, с которыми входят в кинематические пары свободные элементы ее звеньев и не распадающиеся на более простые цепи с нулевой степенью свободы.

Согласно структурной формуле Чебышева, для плоской кинематической цепи число степеней свободы механизма W можно вычислить следующим образом:

, (1.1)

где n – число подвижных звеньев;

р₅ – число пар V класса;

р₄ – число пар IV класса.

Рассмотрим принцип построения механизмов методом наслоения групп Ассура на примере плоского механизма с одной степенью свободы, у которого положение всех звеньев определяется заданием одной обобщенной координаты. Построение механизма начинается с объединения ведущего звена и стойки. Согласно классификации Ассура-Артоболевского, полученный таким образом механизм называется начальным механизмом 1-го класса. Начальный механизм имеет одну степень свободы. Более сложные механизмы образуются присоединением к начальному механизму групп Ассура. В рассматриваемом курсе все группы Ассура будут относиться к группам 2-го класса.

Если механизм имеет в своем составе только группы Ассура 2-го класса, то его следует отнести к механизмам 2-го класса.

Для проведения структурного анализа механизма необходимо выполнить следующие действия:

1. Пронумеровать звенья, определить их количество, дать им название, определить количество кинематических пар IV и V классов.

2. Охарактеризовать заданную кинематическую цепь;

3. Определить число степеней свободы механизма по формуле Чебышева;

4. Выделить группы Ассура 1-го и 2-го классов, определить их количество;

определить класс механизма.

Пример №1. Выполнить структурный анализ механизма, представленного на рис. 1.5.

Решение:

1. Механизм состоит из пяти звеньев: 0 – стойка, 1 – кривошип, 2 – ползун, 3 – кулиса, 4 – шатун, 5 – ползун.

Звено 1 является ведущим звеном. Механизм преобразует вращательное движение кривошипа 1 в поступательное движение ползуна 5. Звенья соединяются друг с другом при помощи семи кинематических пар: 0-1, 1-2, 2-3, 3-0, 3-4, 4-5, 5-0. Все кинематические пары V класса. Кинематических пар IV класса нет.

Рис. 1.5. Иллюстрация к примеру №1

2. Заданная кинематическая цепь является сложной, замкнутой, плоской.

3. Число степеней свободы определяем по формуле Чебышева (1.1):

,

в которой , , 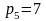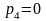. Тогда

Таким образом, механизм обладает одной степенью свободы.

4. Выделим группы Ассура, определим их количество и класс.

4.1. Кривошип 1 является ведущим звеном и в соединении со стойкой 0 образует группу Ассура 1-го класса (рис. 1.6а).

Рис. 1.6. Группы Ассура механизма, рассматриваемого в примере №1

4.2. Кулиса 3 и ползун 2 образуют группу Ассура 2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6.б).

4.3. Шатун 4 и ползун 5 образуют группу Ассура 2-го класса с двумя вращательными и одной поступательной кинематическими парами (рис. 1.6.в).

Таким образом, в механизм входят одна группа Ассура 1-го класса и две группы Ассура 2-го класса.

5. На основании проведенного анализа заключаем, что представленный механизм является плоским механизмом 2-го класса.