
- •Введение
- •Основные понятия теории машин и механизмов
- •Структурный анализ плоских механизмов
- •Классификация кинематических пар
- •Кинематические цепи
- •Определение класса плоских механизмов
- •Кинематический анализ плоского рычажного механизма 2-го класса
- •Метод плана положений
- •Метод планов скоростей
- •Теорема подобия для плана скоростей
- •Метод планов ускорений
- •Теорема подобия для плана ускорений
- •Кинетостатика плоского рычажного механизма
- •Определение инерциальной нагрузки звеньев механизма
- •Графоаналитический метод кинетостатического расчета структурных групп 2-го класса
- •Аналитический метод кинетостатического расчета структурных групп 2-го класса
- •Определение уравновешивающей силы методом Жуковского
- •Расчет на прочность при сложном сопротивлении: плоском изгибе с растяжением (сжатием)
- •Проверка правильности построения эпюр внутренних силовых факторов
- •Задания для контрольных работ №1 и №2 для студентов 3-го курса заочного отделения
- •Исходные данные
- •1. Структурный анализ механизма
- •2. Кинематическое исследование рычажного механизма
- •2.1. Построение планов положений механизма
- •2.2. Построение планов скоростей механизма
- •2.3. Построение плана ускорений механизма в положении 8
- •3. Силовое исследование рычажного механизма
- •3.1. Определение нагрузок
- •3.2. Определение реакций связей
3. Силовое исследование рычажного механизма
3.1. Определение нагрузок
Cилы инерции шатуна 2 и поршня 3:
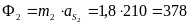 (Н);
(Н);
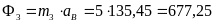 (Н).
(Н).
Момент инерции шатуна 2:
 (кг·м2).
(кг·м2).
Момент сил инерции, действующих на шатун 2:
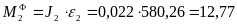 (Н·м).
(Н·м).
Веса звеньев механизма:
Вес
шатуна АВ:  (Н);
(Н);
Вес
поршня 3:  (Н).
(Н).
Сила давления газов в цилиндре, действующая на поршень 3 в положении 8, будет равна:
 (Н).
(Н).
3.2. Определение реакций связей
Рассмотрим
отдельно шатун 2
с поршнем 3,
отсоединив от ведущего звена по шарниру
А.
Вычертим звенья 2-3
в выбранном масштабе, приложим к нему
силы тяжести
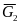 ,
,
 ;
реакции связей в точке А:
;
реакции связей в точке А:
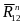 и
и
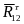 и в точке В:
и в точке В:
 ;
силы инерции
;
силы инерции
 ,
,
 и момент сил инерции
и момент сил инерции
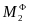 ,
а также силу давления
,
а также силу давления
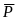 на
поршень 3
(рис. 5, Лист 2).
на
поршень 3
(рис. 5, Лист 2).

Рис. 5. Шатун 2 и поршнень 3 с приложенными силами
Составим для звеньев 2-3 уравнения кинетостатического равновесия в форме моментов:
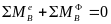 ;
;  ,
,
где  (м);
(м);
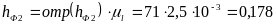 (м).
(м).
Тогда:
 (Н).
(Н).
Уравнение равновесия сил в векторной форме для данной системы сил:
 ;
;  .
.
Неизвестные
величины
и
 найдем графическим способом, построив
план сил звеньев 2-3 (рис. 6, Лист 2). Для
этого из полюса PF
отложим отрезок длиной 50 мм, обозначающий
известную силу
найдем графическим способом, построив
план сил звеньев 2-3 (рис. 6, Лист 2). Для
этого из полюса PF
отложим отрезок длиной 50 мм, обозначающий
известную силу
 .
Тогда масштабный коэффициент для
построения плана сил будет равен:
.
Тогда масштабный коэффициент для
построения плана сил будет равен:
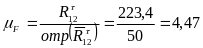 Н/мм.
Н/мм.

Рис. 6. План сил звена АВ
Определим длины отрезков, обозначающих остальные известные силы:
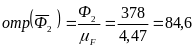 (мм);
(мм);
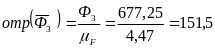 (мм);
(мм);
 (мм);
(мм);
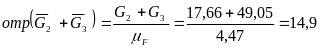 (мм).
(мм).
Зная
линии действия неизвестных
и
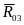 ,
достраиваем план сил, из которого
находим, что:
,
достраиваем план сил, из которого
находим, что:
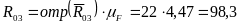 (Н);
(Н);
 (Н).
(Н).
Из
построенного плана сил уточняем
действительные направления сил
и
 :
действительное направление
противоположно первоначально выбранному.
:
действительное направление
противоположно первоначально выбранному.
Перейдем
к рассмотрению равновесия кривошипа 1
(рис. 7, Лист 2). Изобразим его в заданном
положении и покажем действующие на него
силы: реакции связи в точке B:
 и
и
 (причем
(причем
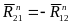 и
и
 );
реакции связи в точке O:
);
реакции связи в точке O:
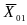 и
и
 ;
а также уравновешивающий момент Mу.
Весом кривошипа пренебрегаем.
;
а также уравновешивающий момент Mу.
Весом кривошипа пренебрегаем.

Рис. 7. Кривошип 1 с приложенными силами
Составим для кривошипа 1 уравнение кинетостатического равновесия в форме моментов:
 ;
; 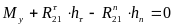 ,
,
где 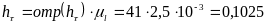 (м);
(м);
 (м).
(м).
Тогда
 (Н·м).
(Н·м).
Величины
 и
и
 найдем, решив графически уравнение:
найдем, решив графически уравнение:
;  .
.
Из
полюса PF
отложим отрезок длиной 240 мм, обозначающий
известную силу
 (рис. 8, Лист 2). Тогда масштабный коэффициент
для построения плана сил будет равен:
(рис. 8, Лист 2). Тогда масштабный коэффициент
для построения плана сил будет равен:
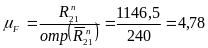 (Н/мм);
а длина отрезка, обозначающего вектор
(Н/мм);
а длина отрезка, обозначающего вектор
 будет равна:
будет равна:
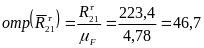 (мм).
(мм).

Рис. 8. План сил для ведущего звена
Из построенного плана сил находим:
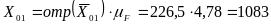 (Н);
(Н);
 (Н).
(Н).
Полная
реакция связи в точке O:
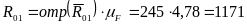 (Н).
(Н).

Лист 1

Лист 2
Список литературы
