Полігон та гістограма частот

Статистичний розподіл вибірки можна задати графічно полігоном або гістограмою частот (відносних частот).

Полігон розподілу вибірки використовується для зображення як дискретних, так і інтервальних варіаційних рядів, а гістограма - лише для інтервальних рядів.

Полігоном частот називають ламану, відрізки якої послідовно з'єднують точки (х₁;n₁), (х₂;n₂),...,(х_k;n_k) координатної площини.

Щ об побудувати полігон частот, на осі абсцис відкладають варіанти х_і, а на осі ординат - відповідні частоти n_і. Далі, точки (х_і;n_і) з'єднують відрізками прямих і отримують полігон частот (рис.1).

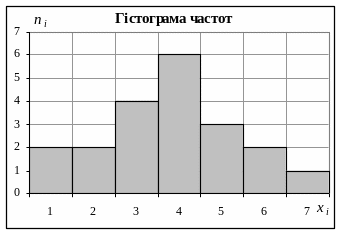
Гістограмою частот називається східчаста фігура, яка складена з прямокутників, основами яких є частинні інтервали [z_і-1,z_і),а їхні висоти n_i.

Емпірична функція розподілу

Нагадаємо, що функція розподілу F(х) випадкової величини Х визначається рівністю

Р(х)=Р{Х<х}.

Її називають ще теоретичною функцією розподілу випадкової величини Х або функцією розподілу генеральної сукупності.

Е мпіричною функцією розподілу випадкової величини Х (функцією розподілу вибірки) називають функцію F_n(х), що визначає для будь-якого дійсного числа х відносну частоту події {Х < х}, тобто

Коли вихідні статистичні дані згруповані в дискретний варіаційний ряд, то емпірична функція розподілу записується у вигляді:

Приклад 2. Знайти емпіричну функцію розподілу за даним розподілом вибірки:

xi	3	5	7	10	15
ni	2	4	7	4	3

Розв’язання.

Для x≤3 F*(x)= 0; для 3<x≤5 F*(x)= 2/20=0,1; для 5<x≤7 F*(x)=(2+4)/20=0,3;

для 7<x≤10 F*(x)=(2+4+7)/20=0,65; для 10<x≤15 F*(x)=(2+4+7+4)/20=0,85;

для 10<x≤15 F*(x)=(2+4+7+4+3)/20=0,85; для 15<x F*(x)=1.

Графік цієї функції:

	1
	0,85
	0,65
	0,3
	0,1
0	1	2	3		4		5		6		7		8		9		10		11		12		13		14		15		16

З апишемо шукану емпіричну функцію:

╚═

Приклад 3. Дано вибірку: 0,1 0,4 0,23 0,12 0,35 0,46 0,11 0.04 0,51 0,27 0,31 0,34 0.09 0,18 0,49 0,33 0,3 0,22 0,14 0,5 0,41 0,25 0,48 0,32 0,29 0,31 0,31 0,46 0,44 0,38 0,39 0,13 0,47 0,4 0,53 0,37 0,16 0,44 0,39 0,27 0,25 0. 46 0,2 0,11 0,32 0,41 0,48 0,22 0,35 0,52

За даними вибірки побудувати інтервальний статистичний розподіл, полігон і гістограму частот.

Розв’язання. Знаходимо обсяг вибірки: n=50.

Для вибору оптимальної довжини частинного інтервалу рекомендована формула:

Згідно цього оптимальна кількість інтервалів:

Фактичну довжину інтервалу знайдемо як

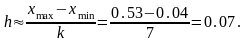
Середина серединного інтервалу Серединою є х₄=0.285_.

Серединний інтервал [z₄; z₅)= [0,25;0,32).

Решту інтервалів знаходимо, рухаючись вперед та назад від серединного:

x₅=x₄+h=0,285+0,07=0,355; x₃=x₄ -h=0,285-0,07=0,215;

x₆=x₅+h=0,355+0,07=0,425; x₂=x₃ -h=0,215-0,07=0,155;

x₇=x₆+h=0,425+0,07=0,495; x₁=x₂ -h=0,155-0,07=0,085;

№ інтервалу i	Частинний інтервал [zi,;zi+1)	Сума частот ni
1	[0,04;0,11).	2
2	[0, 11;0,18).	7
3	[0,18;0,25).	5
4	[0,25;0,32).	11
5	[0,32;0,39).	8
6	[0,39;0,46).	10
7	[0,46;0,53].	7

Отримуємо інтервальний статистичний ряд:

П олігон і гістограма частот.

╚═