Неперервні випадкові величини

Випадкова величина X називається неперервної (НВВ), якщо:

1. множина її значень співпадає з проміжком (кількома проміжками) числової осі, множина може бути обмеженою або необмеженою;

2. ймовірність того, що випадкова величина набуває будь-якого заздалегідь заданого значення х_s , дорівнює нулю.

Зауважимо, що хоча Р{х = х_г} = 0, подія X = х_г є можливою.

Закон розподілу неперервної випадкової величини може бути заданий у вигляді інтегральної функції розподілу F(x)=P{X<x}) або щільності розподілу (щільності ймовірності) f(x).

При числі діапазонів n→∞ дискретна функція розподілу перетворюється в неперервну інтегральну функцію розподілу F(х), зберігаючи всі її властивості.

Функція щільності розподілу ймовірності f(х) являє собою відношення ймовірності влучення неперервної випадкової величини в малий діапазон [х,х+Δх), до довжини цього діапазону Δх: .

Щільність розподілу ймовірності є першою похідною від інтегральної функції розподілу: .

Властивості щільності розподілу: 1) f(х)> 0; 2)

Якщо випадкова величина задана щільністю розподілу, то функцію розподілу можна знайти за формулою

Згідно цього

Приклад 5. Неперервна випадкова величина задана щільністю розподілу . Знайти значення постійної с, інтегральну функцію розподілу F(x), побудувати графіки функцій f(x), F(x).

Розв’язання. Функція f(х) – кусочно-неперервна, її графік - Значення постійної с знаходиться за допомогою властивості щільності розподілу Оскільки f(х) – кусочно-неперервна, то розглядається сума інтегралів на проміжках неперервності:

О тримаємо рівняння , з якого с=2.

Щільність розподілу набуде вигляду:

.

Функція f(х) – кусочно-неперервна, її графік – відрізок прямої (рис.3)

Інтегральну функцію розподілу визначаємо за формулою

При х≤0 ; При 0<х≤1

При х>1

О статочно отримаємо:

Графік F(x) – рис.4

Закони розподілу неперервних випадкових величин

Р івномірний закон розподілу

Щільність розподілу має вигляд

. Графік f(x) – рис.5

І нтегральна функція розподілу має вигляд .

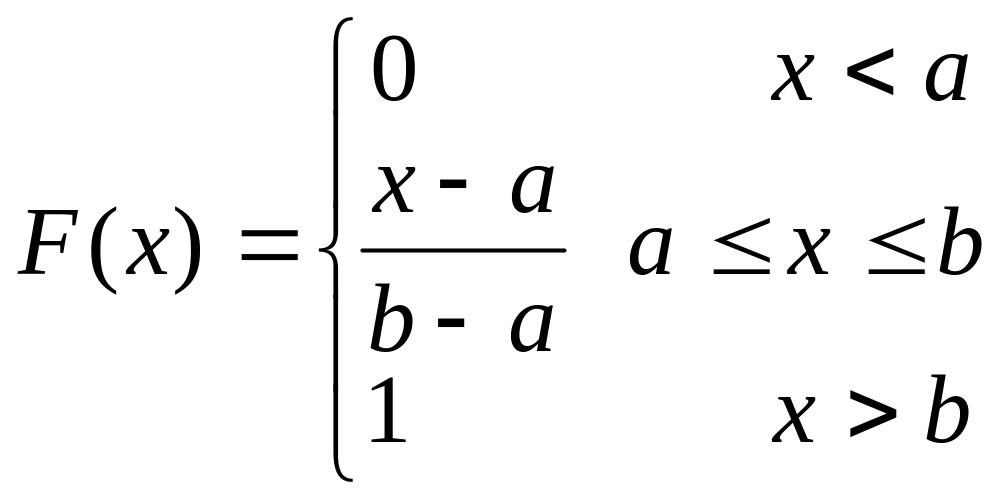Графік F(x) – рис.6

Приклад 6. Тролейбуси прибувають на зупинку кожні 4 хвилини. Визначи­ти ймовірність того, що час очікування тролейбуса не перебільшує 3 хвилин?

Розв'язання. Згідно рівномірного закону розподілу випадкової величини a=0, b=4, X<3,

П оказниковий закон розподілу

Н еперервна випадкова величина розподілена за показовим законом, якщо її щільність розподілу має вигляд: , де  - інтенсивність подій, тобто кількість подій в одиницю часу.

Інтегральна функція випадкової величини, розподіленої за показовим законом, визначається виразом .

Приклад 7. Випадкова величина розподілена за показовим законом з параметром =2. Визначити ймовірність того, що випадкова величина X набуде значення менше за 0,5.

Розв'язання.

Нормальний закон розподілу

Н еперервна випадкова величина розподілена за нормальним законом, якщо її щільність розподілу має вигляд: , де σ і m – параметри розпожілу: m – середнє значення, σ – середнє квадратичне відхилення ВВ.

Інтегральна функція розподілу випадкової величини визначається виразом:

.

Графіки щільності розподілу і інтегральної функції для випадкової величини, розподіленої за нормальним законом, має вигляд, наведений на рисунку.

Приклад 8. Середний час обслуговування ПК t = 2г. Середнє квадратичне відхилення часу обслуговування дорівнює σ_х = 0,403г. Визначити ймовірність завершення обслуговування ПК у термін часу від 1,5 до 2,5 г.

Розв'язання. Так як m = 2, σ = 0,403, а = 1,5 b = 2,5, то

; ; Ф(х₁) = -0,3925; Ф(х₂) = 0,3925;

Р(1,5≤Х≤2,5)= Ф(х₂)- Ф(х₁) = 0,3925