
- •Задание на курсовое проектирование
- •Выбор электродвигателя, кинематический и силовой
- •Выбор материалов зубчатой пары и определение
- •Определение параметров передачи и геометрических
- •Силы в зацеплении передачи,
- •Проверка зубьев колеса на прочность по контактным напряжениям и напряжениям изгиба
- •Проектировочный расчет валов редуктора
- •Конструктивные размеры зубчатой пары
- •Конструктивные размеры корпуса и крышки редуктора
- •Эскизная компоновка редуктора
- •Подбор подшипников и проверка их долговечности
- •Редуктора.
- •Редуктора.
- •Подбор шпонок и проверочный расчет
- •Смазка зацепления и подшипников редуктора
- •Оформление пояснительной записки
- •Приложение а. Электродвигатели асинхронные серии 4а, закрытые обдуваемые гост 19523–81
- •Приложение б. Электродвигатели серии 4а. Исполнение закрытое обдуваемое (по гост 19523 – 81).
- •Приложение в. Подшипники шариковые радиальные однорядные.
- •Приложение г. Подшипники роликовые радиальные с короткими цилиндрическими роликами (гост 8328-75).
- •Приложение д. Крышки врезные с отверстиями и глухие.
- •Приложение к. Значения допусков форм и расположения поверхностей.
- •Приложение л. Посадки основных деталей передач.
- •Приложение м. Шероховатость основных поверхностей.
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •5 . Проверка зубьев колёс по контактным напряжениям
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •5 . Проверка зубьев колёс по контактным напряжениям
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
Определение параметров передачи и геометрических
РАЗМЕРОВ КОЛЕС
Проектные расчеты на контактную прочность и проверочные расчеты на изгиб для прямозубых, косозубых и шевронных передач практически одинаковы, поэтому целесообразно рассматривать их все вместе, выясняя особенности расчета каждого вида передач.
Основной проектной величиной, определяемой из условия прочности, для цилиндрических зубчатых передач, является межосевое расстояние.
Формула для определения межосевого расстояния из условия контактной прочности имеет вид:
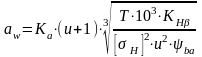 , (16)
, (16)
где 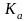 – коэффициент межосевого расстояния,
для прямозубых передач
– коэффициент межосевого расстояния,
для прямозубых передач
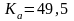 ,
для косозубых и шевронных
,
для косозубых и шевронных
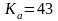 ;
;
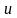 – передаточное число редуктора;
– передаточное число редуктора;
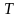 – вращающий момент на ведомом валу
редуктора Нм;
– вращающий момент на ведомом валу
редуктора Нм;
– допускаемые контактные напряжения, МПа;
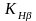 – коэффициент неравномерности
распределения нагрузки по ширине венца,
предварительное значение принимается
по рекомендациям таблицы 6;
– коэффициент неравномерности
распределения нагрузки по ширине венца,
предварительное значение принимается
по рекомендациям таблицы 6;
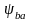 – коэффициент ширины венца колеса по
межосевому расстоянию, принимается в
зависимости от вида колеса из стандартного
ряда (ГОСТ 2185-66):
– коэффициент ширины венца колеса по
межосевому расстоянию, принимается в
зависимости от вида колеса из стандартного
ряда (ГОСТ 2185-66):
0,10; 0,125; 0,16; 0,25; 0,315; 0,40; 0,50; 0,63; 0,80; 1,0; 1,25.
Для прямозубых передач рекомендуются
значения
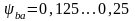 ,
для косозубых –
,
для косозубых –
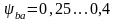 ,
для шевронных –
,
для шевронных –
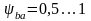 .
Для шевронных зубчатых передач
рекомендуются значения
.
Для шевронных зубчатых передач
рекомендуются значения
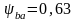 и выше.
и выше.
Вычисленное по формуле 16 значение межосевого расстояния округляется до стандартного по таблице 7.
Предпочтение следует отдавать первому ряду. Значения второго ряда выполняют роль резервных значений, когда к редуктору предъявляются жесткие требования к уменьшению габаритов и массы. Однако это не говорит, о каком-то запрете на использование значений из 2-го ряда.
По выбранному межосевому расстоянию
принимается модуль зацепления
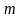 ,
мм, по рекомендации:
,
мм, по рекомендации:
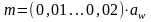 . (17)
. (17)
Значение модуля округляется до стандартного по таблице 7.
Здесь так же следует предпочесть первый ряд значений второму ряду.
Принимать значения
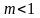 для силовых передач не рекомендуется.
Вообще, надо обратить внимание на тот
факт, что выбрав меньшее значение модуля,
получается большее число зубьев и,
наоборот, приняв большее значение
модуля, получается при расчете меньшее
количество зубьев. В первом случае зуб
будет более мелким, чем во втором.
Соответственно, количество зубьев в
первом случае будет большим, чем во
втором. При уменьшении высоты зуба и
соответствующем увеличении числа зубьев
колеса уменьшается шумность работы,
динамичность нагрузки, но уменьшается
прочность по напряжениям изгиба.
для силовых передач не рекомендуется.
Вообще, надо обратить внимание на тот
факт, что выбрав меньшее значение модуля,
получается большее число зубьев и,
наоборот, приняв большее значение
модуля, получается при расчете меньшее
количество зубьев. В первом случае зуб
будет более мелким, чем во втором.
Соответственно, количество зубьев в
первом случае будет большим, чем во
втором. При уменьшении высоты зуба и
соответствующем увеличении числа зубьев
колеса уменьшается шумность работы,
динамичность нагрузки, но уменьшается
прочность по напряжениям изгиба.
Таблица 6 – Ориентировочные значения коэффициента для зубчатых передач редукторов, работающих при переменной нагрузке
Расположение зубчатых колёс относительно опор |
Твердость НВ поверхностей зубьев |
|
|
>350 |
|
Симметричное |
1,00 – 1,15 |
1,05 – 1,25 |
Несимметричное |
1,10 – 1,25 |
1,15 – 1,35 |
Консольное |
1,20 – 1,35 |
1,25 – 1,45 |
Меньшие
значения принимают для передач с
отношением
|
||
У косозубых передач различают окружной
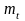 и нормальный
и нормальный
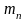 модуль. Нормальный модуль
должен соответствовать стандарту (табл.
7) и является исходной величиной при
геометрических расчётах. Нормальный
модуль
определяют по формуле 17.
модуль. Нормальный модуль
должен соответствовать стандарту (табл.
7) и является исходной величиной при
геометрических расчётах. Нормальный
модуль
определяют по формуле 17.
Таблица 7 – Стандартные значения межосевого расстояния и модуля
Стандартные значения
межосевого расстояния
|
||||||||||||||||||||||||||||||||
1-й ряд |
40 |
50 |
63 |
80 |
100 |
125 |
160 |
200 |
250 |
315 |
400 |
500 |
630 |
800 |
1000 |
1250 |
1600 |
2000 |
2500 |
|||||||||||||
2-й ряд |
71 |
90 |
112 |
140 |
180 |
224 |
280 |
355 |
480 |
560 |
710 |
900 |
1120 |
1400 |
1800 |
2240 |
||||||||||||||||
Стандартные значения модуля , мм (ГОСТ 9563 – 60). |
||||||||||||||||||||||||||||||||
1-й ряд |
1 |
1,25 |
2 |
2,5 |
3 |
4 |
6 |
8 |
10 |
12 |
16 |
20 |
||||||||||||||||||||
2-й ряд |
1,375 |
1,75 |
2,25 |
2,75 |
3,5 |
4,5 |
7 |
9 |
11 |
14 |
18 |
22 |
||||||||||||||||||||
Для непрямозубых передач (косозубых и
шевронных) предварительно задаётся
угол наклона зубьев к образующей цилиндра
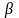 ,
град. Для косозубой передачи предварительно
задаётся угол в пределах 8…18о,
для шевронной передачи – 25…40о.
,
град. Для косозубой передачи предварительно
задаётся угол в пределах 8…18о,
для шевронной передачи – 25…40о.
Далее определяется число зубьев шестерни:
для
прямозубых передач 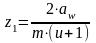 , (18)
, (18)
для
косозубых и шевронных передач 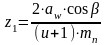 , (19)
, (19)
где – передаточное число редуктора;
–предварительно заданный угол наклона зубьев.
Определение числа зубьев колеса:
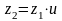 , (20)
, (20)
где – передаточное число редуктора.
Далее уточняется угол наклона зубьев для косозубых и шевронных передач по формуле:
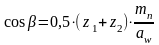 . (21)
. (21)
Угол определяем с точностью до четырёх знаков после запятой.
В дальнейших расчётах необходимо пользоваться уточнённым значением угла наклона зубьев .
Определение основных геометрических размеров передачи.
Диаметры делительных окружностей шестерни и колеса, мм:
для прямозубых передач 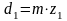 ; (22)
; (22)
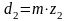 ;
;
для косозубых и шевронных передач 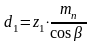 ; (23)
; (23)
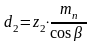 .
.
Определение фактического межосевого расстояния , мм:
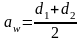 . (24)
. (24)
Диаметры окружностей вершин зубьев шестерни и колеса, мм:
для прямозубых передач 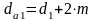 ; (25)
; (25)
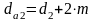 ;
;
для косозубых и шевронных передач 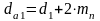 ; (26)
; (26)
 .
.
Диаметр окружностей впадин зубьев шестерни и колеса, мм:
для прямозубых передач  ; (27)
; (27)
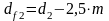 ;
;
для косозубых и шевронных передач 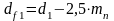 ; (28)
; (28)
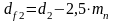 .
.
Ширина венца колеса, мм:
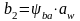 . (29)
. (29)
Ширина венца шестерни, мм:
для прямозубых передач  ; (30)
; (30)
для косозубых и шевронных передач  . (31)
. (31)

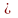 350
350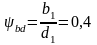 ;
при увеличении
;
при увеличении
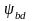 до
до
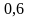 для консольно расположенных колёс и
до
для консольно расположенных колёс и
до
 при несимметричном расположении их
следует принимать большие из указанных
в таблице значений
.
При постоянной нагрузке
при несимметричном расположении их
следует принимать большие из указанных
в таблице значений
.
При постоянной нагрузке
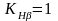 .
.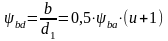 .
.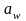 ,
мм (ГОСТ 2185 –
66).
,
мм (ГОСТ 2185 –
66).