
- •Задание на курсовое проектирование
- •Выбор электродвигателя, кинематический и силовой
- •Выбор материалов зубчатой пары и определение
- •Определение параметров передачи и геометрических
- •Силы в зацеплении передачи,
- •Проверка зубьев колеса на прочность по контактным напряжениям и напряжениям изгиба
- •Проектировочный расчет валов редуктора
- •Конструктивные размеры зубчатой пары
- •Конструктивные размеры корпуса и крышки редуктора
- •Эскизная компоновка редуктора
- •Подбор подшипников и проверка их долговечности
- •Редуктора.
- •Редуктора.
- •Подбор шпонок и проверочный расчет
- •Смазка зацепления и подшипников редуктора
- •Оформление пояснительной записки
- •Приложение а. Электродвигатели асинхронные серии 4а, закрытые обдуваемые гост 19523–81
- •Приложение б. Электродвигатели серии 4а. Исполнение закрытое обдуваемое (по гост 19523 – 81).
- •Приложение в. Подшипники шариковые радиальные однорядные.
- •Приложение г. Подшипники роликовые радиальные с короткими цилиндрическими роликами (гост 8328-75).
- •Приложение д. Крышки врезные с отверстиями и глухие.
- •Приложение к. Значения допусков форм и расположения поверхностей.
- •Приложение л. Посадки основных деталей передач.
- •Приложение м. Шероховатость основных поверхностей.
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •5 . Проверка зубьев колёс по контактным напряжениям
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
- •Расчет цилиндрического одноступенчатого редуктора с косозубым зацеплением Ведомость проекта
- •1. Выбор электродвигателя, кинематический и силовой
- •2 . Выбор материала зубчатой пары
- •3 . Определение параметров передачи
- •4 . Усилия в зацеплении передачи
- •5 . Проверка зубьев колёс по контактным напряжениям
- •6 . Проектировочный Расчет валов редуктора
- •7 . Конструктивные размеры зубчатой пары
- •8 . Конструктивные размеры корпуса и крышки редуктора
- •9 . Подбор подшипников и проверка их долговечности
- •1 1. Смазка зацепления и подшипников редуктора
3 . Определение параметров передачи
И ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ КОЛЁС
Определяем межосевое расстояние закрытой передачи из условия контактной прочности, мм:
, (3.1)
где – коэффициент межосевого расстояния, для шевронных передач (стр. 11, /1/);
– передаточное число редуктора;
– вращающий момент на ведомом валу редуктора, Н м;
– коэффициент
неравномерности распределения нагрузки
по ширине венца,
 (стр. 12, /1/);
(стр. 12, /1/);
– коэффициент
ширины венца колеса, принимаем для
шевронной передачи
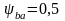 (стр. 11, /1/).
(стр. 11, /1/).
 мм.
мм.
Округляем до
ближайшего значения, используя ряд
нормальных линейных размеров ГОСТ
2185-66 (стр. 12, /1/):
 мм.
мм.
Определяем нормальный модуль зацепления, мм:
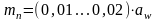 (3.2)
(3.2)
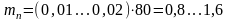 мм.
мм.
По ГОСТ 9563-60 (стр.
12, /1/) принимаем
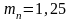 мм.
мм.
Предварительно
принимаем угол наклона зубьев
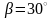 .
.
Определяем число зубьев шестерни:
 , (3.3)
, (3.3)
где – передаточное число редуктора;
 .
.
Принимаем
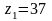 .
.
Определяем число зубьев колеса:
, (3.4)
где – передаточное число редуктора;
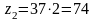 .
.
Уточняем угол наклона зубьев:
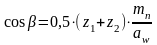 . (3.5)
. (3.5)
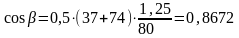 .
.

КП. 12. 2-74 06 01. 1. 112м. 03. ПЗ
11
Определяем делительный диаметр шестерни и колеса, мм:
 , (3.6)
, (3.6)
где – уточнённый угол наклона зубьев, град.
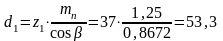 мм;
мм;
 мм.
мм.
Определяем фактическое межосевое расстояние, мм:
; (3.7)
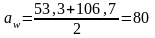 мм.
мм.
О пределяем
диаметр вершин зубьев шестерни и колеса,
мм:
пределяем
диаметр вершин зубьев шестерни и колеса,
мм:
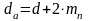 ; (3.8)
; (3.8)
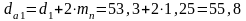 мм;
мм;
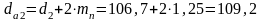 мм.
мм.
Определяем диаметр впадин зубьев шестерни и колеса, мм:
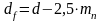 ; (3.9)
; (3.9)
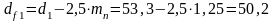 мм;
мм;
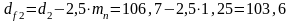 мм.
мм.
Определяем ширину венца колеса, мм:
; (3.10)
 мм.
мм.
Определяем ширину венца шестерни, мм:
; (3.11)
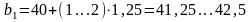 мм.
мм.
Принимаем
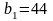 мм.
мм.
КП. 11. 2-74 06 01. 3. 31мп. 03. ПЗ
12
КП. 12. 2-74 06 01. 1. 112м. 03. ПЗ
12
4 . Усилия в зацеплении передачи
В зацеплении шевронной передачи действуют усилия:
– окружная сила, Н;
– радиальная сила, Н.
, (4.1)
где – вращающий момент на ведомом валу редуктора, Н м;
– делительный диаметр колеса, мм.
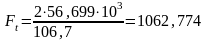 Н.
Н.
; (4.2)
где – угол эвольвентного зацепления, ;
– уточнённый угол наклона зубьев, град.
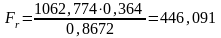 Н.
Н.

Рис. 4.1. Схема сил в зацеплении.
14
КП. 12. 2-74 06 01. 1. 112м. 04. ПЗ
КП. 12. 2-74 06 01. 1. 112м. 04. ПЗ
13
5 . Проверка зубьев колёс по контактным напряжениям
И НАПРЯЖЕНИЯМ ИЗГИБА
Определяем окружную скорость, м/с:
, (5.1)
где – угловая скорость ведомого вала редуктора, рад/с;
– делительный диаметр колеса, мм.
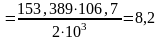 м/с.
м/с.
Определяем степень
точности. При окружной скорости
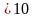 м/с
(для шевронных цилиндрических передач)
принимаем 8 степень точности (стр. 17,
/1/).
м/с
(для шевронных цилиндрических передач)
принимаем 8 степень точности (стр. 17,
/1/).
Определяем отношение
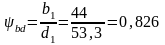 .
.
Определяем расчётные контактные напряжения, МПа:
, (5.2)
где – межосевое расстояние, мм;
– вращающий момент на ведомом валу редуктора, Н м;
– коэффициент нагрузки;
– передаточное число редуктора;
– ширина венца зубчатого колеса, мм.
Определяем коэффициент нагрузки:
, (5.3)
где
– коэффициент
учитывающий неравномерность распределения
нагрузки между зубьями,
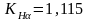 (стр. 18,
/1/);
(стр. 18,
/1/);
– коэффициент
неравномерности распределения нагрузки
по ширине венца,
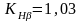 (стр. 18, /1/);
(стр. 18, /1/);
– динамический
коэффициент,
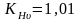 (стр. 19,
/1/).
(стр. 19,
/1/).
 .
.
 МПа
МПа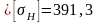 МПа.
МПа.
Определяем отклонение значения расчётного контактного напряжения от допускаемого по формуле:
. (5.4)
Е сли получится отрицательное значение, то имеет место недогрузка, а если положительное – перегрузка. Допускается недогрузка передачи до 10% и перегрузка – до 5% (стр. 65, /3/).
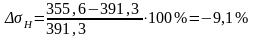 .
.
14
КП. 12. 2-74 06 01. 1. 112м. 05. ПЗ
О тклонение допустимо. Но в целях экономии материала целесообразно уменьшить ширину венца колеса редуктора.
Принимаем
 мм.
Тогда:
мм.
Тогда:
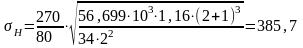 МПа
МПа.
МПа
МПа.
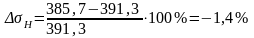 .
.
Отклонение допустимо.
Окончательно принимаем мм, тогда:
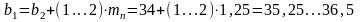 мм.
мм.
Принимаем
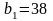 мм.
мм.
Определяем расчётные напряжения изгиба, МПа:
, (5.5)
где – окружная сила в зацеплении, Н;
– коэффициент нагрузки;
– коэффициент, учитывающий форму зуба;
– нормальный модуль зацепления, мм;
– ширина венца зубчатого колеса, которое будем проверять на изгиб, мм;
– коэффициент, учитывающий неравномерность распределения нагрузки между зубьями, (стр. 21, /1/);
– коэффициент для компенсации погрешности.
Определяем коэффициент нагрузки:
, (5.6)
где
– коэффициент, учитывающий неравномерность
распределения нагрузки по длине зуба,
 (стр. 20, /1/);
(стр. 20, /1/);
– динамический
коэффициент,
 (стр. 20, /1/).
(стр. 20, /1/).
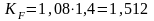 .
.
Определяем коэффициент компенсации погрешности:
, (5.7)
где – уточнённый угол наклона зубьев, град.
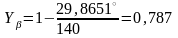 .
.
Определяем эквивалентное количество зубьев шестерни и колеса:
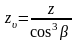 , (5.8)
, (5.8)
где – уточнённый угол наклона зубьев, град.
15
КП. 12. 2-74 06 01. 1. 112м. 05. ПЗ
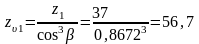 ;
;
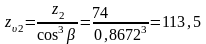 .
.
Коэффициент формы зуба определяем отдельно для шестерни и колеса (стр. 20, /1/):
 ;
; 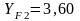 .
.
О пределяем отношение:
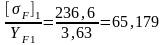 МПа;
МПа;
 МПа.
МПа.
Проверяем на изгиб зубья колеса, так как для них отношение меньше.
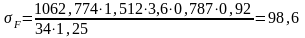 МПа
МПа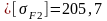 МПа.
МПа.
Расчётное напряжение на изгиб значительно меньше допускаемого – это допустимо, так как нагрузочная способность большинства передач ограничивается контактной прочностью.
Прочность зубьев обеспечена.
КП. 12. 2-74 06 01. 1. 112м. 05. ПЗ
16
