Зображення фігур у стереометрії

1. Зображенням фігури називається будь-яка фігура, подібна паралельній проекції даної фігури. При цьому маються на увазі невироджені проекції, які дають змогу однозначно визначити форму зображуваної фігури. Паралельною проекцією куба мо­же бути квадрат або прямокутник з двома відрізками. А такі зображення не наочні і незрозумілі. Адже існує безліч різних геометричних тіл, відмінних від куба, що мають такі самі про­екції.

Щоб зображення фігури було зрозумілішим, з усіх можли­вих її проекцій вибирають такі, на яких є зображення всіх її частин. При цьому «невидимі» лінії (розташовані за іншими частинами фігури) зображають штриховими лініями.

2. Щоб правильно виконувати зображення, бажано знати, якими можуть бути зображення найпоширеніших плоских фігур.

Зображення паралелограма може бути будь-який інший паралелограм, оскільки при паралельному проектуванні паралельні відрізки відображаються на паралельні відрізки. Зокрема, ромб, прямокутника, квадрат можна зображати будь-яким паралелограмом. І навпаки, будь – який паралелограм можна зображати у вигляді квадрата, ромба, прямокутника чи іншого паралелограма.

Зображенням трапеції може бути будь-яка інша трапеція з таким самим відношенням довжин основ, оскільки при пара­лельному проектуванні відношення довжин паралельних відрізків зберігаються.

Зображенням будь-якого трикутника може бути довільний трикутник. І будь-який трикутник може бути зображенням безлічі інших трикутників. Зокрема, будь-який трикутник можна зображати у вигляді трикутника правильного, рівнобедреного, прямокутного, тупокутного чи гострокутного.

Правильний шестикутник можна зо­бражати довільним шестикутником, кожна сторона якого паралельна проти­лежній стороні і одній з діагоналей, що проходить через центр шестикутника.

Проекція многокутника – многокутник або відрізок.

Проекція кола може бути коло, еліпс або відрізок. Проекція того самого кола може бути різною залежно від кута між площиною проекцій і площиною кола.

Тема: Ортогональне проектування

1. Якщо проектуючи прямі перпендикулярні до площини проекцій, то таке проектування називають прямокутним, або ортогональним.

Ортогональне проектування - окремий вид паралельного проектування, тому воно має всі властивості паралельного про­ектування. У кресленні воно - основне. І ми, говорячи далі про проекції, матимемо на увазі тільки ортогональні проекції. Тоб­то проекцією точки називатимемо основу перпендикуляра, опущеного з даної точки на площину. Якщо точка лежить на площині проекцій, то вона збігається зі своєю проекцією.

Проекцією фігури на площину називають множину проекцій усіх точок даної фігури на дану площину. Зокрема, проекцією n - кутника є n-кутник (якщо площини проекцій і многокутни­ка не перпендикулярні).

2. Теорема. Площа проекції многокутника дорівнює площі проектованого многокутника, помноженій на косинус кута між їх площинами.

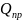3. Наслідок. Якщо S і Q – площі многокутників площини , а і – площі їх проекцій на площину , то : .

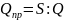Поняття проектування, паралельне проектування і ортогональне проектування пов'язані між собою.

Тобто ортогональне проектування – окремий вид паралельного проектування, а паралельне проектування - вид проектування. Інший вид останнього - центральне проек­тування (перспектива).

Зображати фігури при ортогональному проектуванні можна різними способами, докладно їх розглядають у кресленні і нарисній геометрії.