Мішаний добуток векторів

І. Нехай:

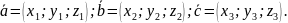
1. За означенням мішаного добутку: .

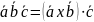2. Мішаний добуток векторів через координати:

3. Властивості мішаного добутку;

;

;

- компланарні.

4. Застосування мішаного добутку:

а) Знаходження об’єма паралелепіпеда: .

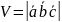б) Об’єм трикутної піраміди, побудованої на векторах

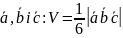
Тема: Аксіоми планіметрії

Основне в геометрії - її поняття і твердження. Для більшості понять формулюються означення, але існують поняття неозначувані. Це - точка, пряма, площи­на та деякі інші.

Переважну більшість геометричних тверджень доводять, тобто показують, що вони як логічні наслідки випливають з інших істинних тверджень. А як бути, коли на початку курсу ще немає «інших тверджень»? У цих випадках кілька твер­джень приймають за істинні без доведень. їх називають аксіо­мами. А твердження, що доводяться, - теоремами.

Для планіметрії можна обирати різні системи аксіом. Одна з них може бути такою:

1. Яка б не була пряма, існують точки, що належать цій, прямій, і точки, що їй не належать.

2. Через будь-які дві різні точки можна провести пряму і тільки одну.

3. З трьох точок прямої одна і тільки одна лежить між двома іншими.

4. Кожний відрізок має певну довжину.

5. Кожний кут має певну міру.

6. Пряма розбиває площину на дві півплощини.

7. На будь-якій прямій від заданої точки у заданому напря­мі можна відкласти відрізок даної довжини і тільки один.

8. Від будь-якого променя у даній півплощині можна від­класти даний кут з вершиною у початку променя і тіль­ки один.

9. Який би не був трикутник, існує рівний йому трикут­ник у заданому розміщенні відносно заданої прямої.

10. Через точку, що не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній прямій (аксіома Евкліда).

Тема: Паралельне проектування. Зображення фігур в стереометрії

1. Геометри для зображення просторових фігур на площині частіше користуються пара­лельним проектуванням. Наочне уявлення про нього дає утворення тіні від предмета, освітлюваного паралельними променями. Уявіть, що через кожну точку фігури К проведено прямі, паралельні якійсь прямій l до перетину з площиною . Множина К₁ точок перетину всіх таких прямих із площиною є паралельною проекцією фігури К на площині . Тут — площина проекцій, а прямі, па­ралельні l, - проектуючі прямі.

2. Властивості паралельного проектування випливають з такої теореми.

Теорема. Якщо відрізки, які проектуються, не паралельні проектуючій прямій, то при паралельному проектуванні:

1.відрізки фігури зображуються відрізками;

2. паралельні відрізки — паралельними відрізками або відрізками однієї прямої;

3.довжини проекцій паралельних відрізків або відрізків од­нієї прямої відносяться, як довжини проектованих відрізків.

3. Доведення цієї теореми досить громіздке, тому ми його не наводимо. Третю частину теореми (якщо А₁В₁ і С₁D₁ – проекції паралельних відрізків АВ і СD, то А₁В₁ : С₁D₁=АВ:СD) проілюстровано малюнками.

а) б)

4. Якщо хоч одна проектуючи пряма лежить у площині плоскої фігури, то проекцію такої фігури є точка, відрізок, промінь чи пряма. Зокрема, проекцію трикутника, довільного многокутника, кола і круга може бути відрізок.