Тема: Неперервність функції
1. Якщо функцію задано не деякому проміжку та його графік на ньому є нерозривною лінією, то функція називається неперервною на цьому проміжку.
2
.
Приклади неперервних функцій:
а) б) в)
3
.
Про функцію
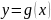кажуть що вона в т. х0
має розрив, тобто не є неперервною, або
розривна.
4. Точка розриву може належати до області визначення, але може і не належати:
а) п. 3 функція , точка розриву належить Д(у), та відповідає значенню а.
б) Приклади коли точка розриву не належить Д(у):
1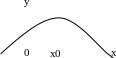
)
2)
5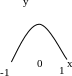
.
Дослідити на неперервність:
а) б) в) г)
Тема: Гармонічні коливання
1.
Величини, що змінюються за законом
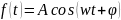або
.
Відіграють важливу роль у фізиці за таким законом змінюється координата кульки, прикріпленої до пружини. Говорять, що кулька здійснює гармонічні коливання.
2.
Параметри А, w,
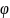мають спеціальні назви.
а) А – амплітуда коливання, яка характеризує величину найбільшого відхилення від положення рівноваги.
б) w –
кутова швидкість обертання точки,
кількість повних коливань за 2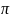
одиниць часу (за 1 оборот).
в) - початкова фаза коливання;
г) wt + φ - фаза коливання.
3. Час
протягом якого точка робить повний
оборот називається періодом гармонічного
коливання
.
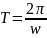4. Приклад: Визначте амплітуду, фазу, початкову фазу, кутову швидкість, період гармонічного коливання заданого формулою:
а)
Розв'язання:
А = 6; wt
+
=
;
;
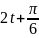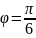w = 2; Т =
б)
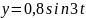
Розв'язання:
А=0,8;
;
;
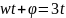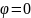w = 3;
.
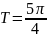Тема: Розв’язання рівнянь заміною невідомої
І. Методичні вказівки
Деякі алгебраїчні рівняння зводяться до квадратних або до рівнянь вищих степенів за допомогою заміни змінних .
Розглянемо на прикладах:
1. Біквадратне рівняння:
;
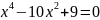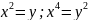робимо
підстановку
;
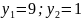далі:
;
.
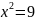
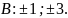
2. Показникові рівняння:
;
;
;
;
;
;
;
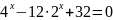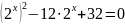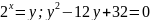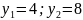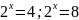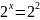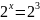х=2; х=3 В: (2;3).
3. Логарифмічне рівняння:
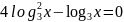
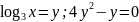
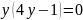
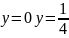
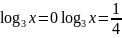
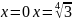В:
(0;
)
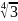4. Тригонометричні рівняння:
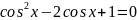
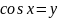
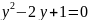
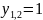
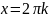В:
(2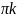
)
ІІ. Самостійне розв’язання рівнянь:
Розв’язати рівняння:
1.
;
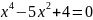
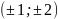2.
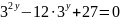(1; 2);
3.
;
4.
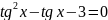
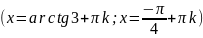
Тема: Розв’язання текстових задач
І. Методичні вказівки:
1. Вказівки до рішення текстових завдань
а) Як правило, за невідомих слід приймати шукані величини.
б) Набор невідомих має бути достатнім для перекладу умов завдання мовою математичних співвідношень.
в) Вибравши невідомі, в процесі переведення умов завдання в рівняння необхідно використовувати всі дані і умови завдання.
2. Алгоритм вирішення текстових задач:
а) Введення змінних, тобто позначення буквами х,в,z… величини, які потрібно знайти по умові завдання.
б) Переклад умов завдання мовою математичних співвідношень, тобто складання рівнянь.
в) Вирішення рівнянь.
г) Перевірка отриманих рішень на виконання умов завдання.
ІІ. Завдання:
Задача № 1
Час, що його витрачає автобус на подолання відстані 325 км, за новим розкладом руху автобусів скорочено на 40 хв. Знайдіть середню швидкість руху автобуса за новим розкладом, якщо вона на 10 км/год більша від середньої швидкості, передбаченої старим розкладом.
Задача № 2
Моторний
човен, швидкість якого в стоячій воді
становить 15 км/год, пройшов униз за
течією
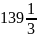км і повернувся назад. Визначте швидкість
течії річки, якщо на весь шлях витрачено
20 год.
Задача № 3
Поїзд мав пройти 220 км за певний час. Через 2 год після початку руху його було затримано на 10 хв і, щоб своєчасно прийти в пункт призначення, поїзд збільшив швидкість на 5 км/год. Знайдіть початкову швидкість поїзда.
Задача № 4
Після зустрічі двох теплоходів один з них пішов на південь, а другий — на захід. Через 2 год після зустрічі відстань між ними була 60 км. Знайдіть швидкість кожного теплохода, якщо відомо, що швидкість одного з них на
6 км/год більша від швидкості другого.
Задача № 5
Два тіла рухаються назустріч один одному з двох точок, відстань між якими 390 м. Одне тіло пройшло за першу секунду 6 м, а за кожну наступну проходило на 6 м більше ніж за попередню. Друге тіло рухалось рівномірно із швидкістю 12 м/с і почало рух через 5 с після першого. Через скільки секунд після того, як почало рухатись перше тіло, вони зустрінуться?
Задача № 6
На будівництві залізничної магістралі бригада будівельників за кілька днів повинна була за планом перемістити 2160 м3 ґрунту. Перші 3 дні бригада виконувала щодня встановлену норму, а потім щодня перевиконувала її на
80 м3; тому вже за день до строку бригада перемістила 2320 м3 ґрунту. Яка за
планом денна норма бригади?
Задача № 7
Дві бригади школярів, працюючи разом, закінчили садити дерева на навчально-дослідній ділянці за 4 дні. Скільки днів витратила б на виконання цієї роботи кожна бригада, якби одна з них могла закінчити садіння дерен на б днів швидше, ніж друга?
Задача № 8
Для перевезення 60 т вантажу викликали деяку кількість машин. У зв'язку з тим, що на кожну машину вантажили на 0,5 т менше від запланованого, додатково було викликано ще 4 машини. Скільки машин було заплановано спочатку?