3. Методичні рекомендації

3.1. Як працювати над книгою

1. Перед вивченням теми потрібно уважно ознайомитись із змістом навчальних завдань.

2. Рекомендуємо при вивченні матеріалу навчальних завдань дотримуватись такого порядку:

1. Ознайомитись з темою, метою завдання.

2. Вивчити основний матеріал за підручником.

3. Виконати практичні вправи.

3. Як читати підручник? Читання книго з метою вивчення дисципліни ніколи не обмежується одна розовим читанням.

Працюючи над підручником, рекомендується прочитати спочатку весь параграф книги. Потім слід читати раз, але по окремих частинах, вдумуючись в кожне питання, положення, щоб повністю зрозуміти прочитане.

Якщо зустрічаються незрозумілі слова, окремі твердження, малюнки, формули, треба за допомогою словників, довідників вияснити незрозуміле.

Глибоко і надовго можна засвоїти тільки те, що добре продумане і усвідомлене.

Вчиться читати швидко: надто повільне читання призводить до розриву зв’язків між прочитаним.

При повторному читанні рекомендується складати конспект.

3.2. Як складати конспект

1. Конспект являє собою короткий зв’язний переказ матеріалу, що вивчається, розчленований заголовками і підзаголовками за планом.

Конспект допомагає запам’ятати прочитане і в майбутньому відновити його в пам’яті.

Матеріал, який конспектується, треба добре продумати, а записи проводити старанно слідкуючи, щоб не спотворити думки.

2. При опрацюванні підручників, де є графіки, схеми, таблиці, слід добре в них розібратись і головне з них внести в конспект.

3. Не намагайтесь механічно, без глибокого розуміння, завчити формули, бо це не дає бажаних наслідків. Старайтесь формулу осмислити.

4. Конспектування не тільки сприяє запам’ятовування прочитаного, а й є найголовнішим прийомом самостійної роботи над підручником.

Щоб найдовше зберегти осмислений і вивчений матеріал у пам’яті, слід періодично його повторювати за складеним Вами конспектом.

Систематичне повторення приводить до економії часу, бо затрати часу на повторення будуть весь час зменшуватись.

Не покладайтесь на свою пам’ять, яка б вона добра не була. Конспектуйте матеріал, який вивчаєте самостійно за підручником, доповнюйте свої конспекти, читаючи додаткову літературу .

4. Опорні конспекти Тема: Відсоткові розрахунки

І. Означення: відсотком будь-якого числа називається сота частина цього числа.

ІІ. Типи перетворень з відсотками:

1. Подати у вигляді дробу задане число відсотків.

Завдання розв’язується приписуванням знаменника 100 до даного числа відсотків, число відсотків є чисельником. Наприклад,

; .

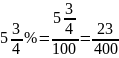2. Виразити у відсотках звичайний дріб.

Для цього звичайний дріб слід перетворити у десятковий з точністю до 0,01; цей дріб, помножений на 100, дорівнює кількості відсотків. Наприклад,

.

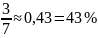ІІІ. Три типи задач на відсотки.

1. Знайти p% від числа .

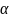Задача зводиться до знаходження дробу від числа і розв’язується множенням на цей дріб: х .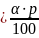

2. Знайти число, якщо p% від нього дорівнює b.

Задача зводиться до знаходження числа за даною величиною b його дробу . Задача розв’язується діленням на цей дріб: х .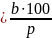

3. Знайти, скільки відсотків складає число b від числа .

Необхідно виразити у відсотках відношення числа b до : х .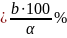

ІV. Прості і складні відсотки.

1. Прості відсотки

Відсотки називаються простими, якщо відсотки на відсотки не нараховуються.

2. Складні відсотки – їх нараховують не тільки на основну суму, а й нараховані раніше відсотки.

Формула складних відсотків:

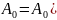
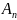- початковий капітал;

n – роки;

p – відсоток річних;

- нарощений капітал.