Лекции по АиГ / Alg_03

Многочлены.

Деление с остатком; корни и их кратности.

Как известно, выражение называется одночленом от неизвестных x₁,…,x_n. Здесь коэффициент a может быть любым элементом из некоторого фиксированного числового поля k. Число k₁+…+k_n называется степенью одночлена. Сумма нескольких таких одночленов называется многочленом p(x₁,…, x_n) от тех же неизвестных. Степенью многочлена deg p называется наибольшая из степеней одночленов, которые входят в него с ненулевым коэффициентом. Если же все коэффициенты многочлена равны 0, ему приписывается степень (-¥). Если считать, что справедливы равенства (-¥)+n = (-¥) и (-¥)+(-¥) = (-¥), то всегда выполняется сотношение deg (pq) = deg p+degq. Совокупность всех многочленов отнеизвестных x₁, …, x_n с коэффициентами из поля k обозначается k[x₁, …, x_n].

В дальнейшем, если не оговорено противное, будут рассматриваться многочлены от одного неизвестного.

В отличие от операций сложения (вычитания) и умножения, операция деления для многочленов определена не всегда. Запись p|q (p делит q) означает существование такого многочлена s, что q = ps. Зато (для многочленов от 1 неизвестного) всегда выполнимо деление с остатком.

Теорема.

Пусть q любой, а p ненулевой многочлен. Тогда существуют и определены однозначно такие многочлены s (неполное частное) и r (остаток), что:

1. q = ps+r

2. deg r<deg p.

Доказательство.

Если deg q = (-¥), то есть q º 0, то результат очевиден. Если deg q < deg p, то берем s = 0, r = q. Предположим, что для многочленов степени меньше n существование s и q уже доказано. Пусть n = deg q³deg p = m. По условию q = axⁿ +…, p = bx^m + …, причем b¹0. Возьмем q₁ = q-a/bx^n-mp. Тогда deg q₁<n и по предположению индукции q₁ = ps₁ + r,где deg r<deg p. Но, тогда q = q₁ + a/bx^n-mp = p(s₁ + a/bx^n-m) + r, что и требовалось.

Докажем единственность. Пусть q = ps₁ + r₁ = ps₂ + r₂. Отсюда вытекает, что

p(s₁-s₂) = r₂-r₁. Если многочлен в скобках не нулевой, то левая часть формулы имеет степень не меньше, чем deg p, в то время как правая – строго меньше того же числа. Следовательно, s₁ º s₂, а тогда и r₁ º r₂.

На практике нахождение неполного частного и остатка производится известным способом “деления углом”.

Следствие (формула Безу).

Для всякого многочлена p и любого aÎk существует такой многочлен s, что:

p(x) = p(a)+(x-a)s(x).

В самом деле, разделим p на (x-a) с остатком: p(x) = (x-a)s(x)+r. Тогда deg r £0. Положим x = a. Тогда находим r = p(a).

Из формулы Безу вытекает, что элемент aÎk является корнем многочлена p, то есть p(a) = 0, тогда и только тогда, когда (x-a)|p. Дадим определение кратности корня многочлена.

Определение.

Элемент aÎk называется корнем многочлена p кратности m, если (x-a)^m|p, но

. (Иногда удобно допускать m = 0; корень степени 0 характеризуется условием: p(a)¹0).

Теорема.

Пусть p = uv и u(a)¹0. Тогда кратности корня a у многочленов p и v совпадают.

Доказательство.

Пусть m – кратность корня a у многочлена p, а t – кратность того же корня у многочлена v. Имеем: p = (x-a)^mp₁, v = (x-a)^tv₁. Предположим, что m>t. Тогда

(x-a)^t((x-a)^m-tp₁-uv₁) = 0. Следовательно, многочлен, стоящий во второй скобке, равен 0. Положим в этом многочлене x = a. Тогда получаем: u(a)v₁(a) = 0, откуда следует, что v₁(a) = 0. По формуле Безу v₁ = (x-a)v₂. Но тогда v = (x-a)^t+1v₂, что противоречит определению кратности корня многочлена v. Точно также к противоречию приводит и предположение m<t. Теорема доказана.

Следствие

Если a₁, a₂, …, a_k – попарно различные корни многочлена p и m₁, m₂,…, m_k – их кратности, то .

В частности, m₁+m₂+…+m_k£deg p, что формулируют так: многочлен степени n³0 имеет не более n корней с учетом их кратностей.

Дифференцирование многочленов.

В математическом анализе производная от любой функции f(x) (в частности от многочлена) определяется как предел = . Операция перехода к пределу не относится к числу алгебраических и определена не для всех числовых полей. Однако нахождение производной от многочлена p и не требует предельного перехода. Выражение q(x, t) = p(x+t)-p(x) представляет собой многочлен от двух неизвестных x и t, который можно записать в виде:

q(x, t) = q₀(x)+q₁(x)t+…+q_n(x)tⁿ, где q_i(x)Îk[x]. Положив в этой формуле t = 0, получим, что q₀(x) = 0. Следовательно, q(x, t)/t = q₁(x)+…+q_n(x)t^n-1. Многочлен q₁(x) и называется производной от p(x). Можно записать: . Здесь важен порядок действий: в начале производится операция деления на t, а потом в полученном выражении полагаем t = 0. Такое определение производной пригодно уже для любого поля k и, в то же время, для поля действительных чисел получается тот же результат, что и в анализе. По этой причине сохраняются все известные из анализа “правила дифференцирования”, например, формула дифференцирования произведения, формула Тейлора для многочленов и т.д. Отметим еще, что такой “алгебраический” подход можно перенести с многочленов на рациональные функции.

Понятие призводной можно применить, например, к нахождению кратностей корней многочлена.

Теорема.

Всякий корень многочлена p кратности m>0, является корнем производной кратности (m-1).

Доказательство.

По условию p(x) = (x-a)^ms(x), причем s(a)¹0. Отсюда: = m(x-a)^m-1s(x)+(x-a)^m. Следовательно, (x-a)^m-1|, но , что и требовалось.

Следствие.

Число a является корнем многочлена p кратности m тогда и только тогда, когда .

Интерполирование.

Пусть фиксировано некоторое числовое поле k. Назовем спектром S произвольный набор попарно различных элементов a₁, …,a_p этого поля (узлы интерполяции) и положительных целых чисел m₁, …,m_p (кратности узлов).

Говорят, что для данного спектра поставлена задача интерполяции, если задана таблица значений T, то есть для каждого элемента a спектра кратности m указано m элементов b⁽⁰⁾, …,b^(m-1) из того же поля k.

Многочлен pÎk[x] решает поставленную задачу интерполяции, если для всякого aÎS выполняются условия: p(a) = b⁽⁰⁾, = b⁽¹⁾, …,p^(m-1)(a) = b^(m-1), что записывается в виде: p(S) = T. Такой многочлен называется интерполяционным.

Каждому спектру S поставим в соответствие многочлен p_S, равный . Этот многочлен удовлетворяет условиям p_S(S) = O и имеет степень m₁+m₂+…+m_p = |S|. Если любой интерполяционный многочлен p разделить на p_S с остатком p = qp_S+r, то многочлен r также будет интерполяционным. Следовательно, если задача интерполяции имеет решение, то существует и интерполяционный многочлен степени меньше, чем |S|. Если p₁ и p₂ два таких многочлена, то число корней их разности с учетом кратностей не меньше, чем |S| и потому p₁-p₂º0. Итак, если задача интерполяции имеет решение, то существует единственный интерполяционный многочлен степени не выше |S|-1. Он называется многочленом Лагранжа-Сильвестра.

Теорема.

Для всякой задачи интерполяции существует многочлен Лагранжа-Сильвестра.

Доказательство.

Положим L = , где x_i – неизвестные элементы из поля k. Тогда каждое из равенств L^(k)(a) = b^(k), k = 0, 1,…,(m-1); aÎS, представляет собой линейное уравнение с |S| неизвестными с правой частью b^(k). Общее число уравнений равно |S|, то есть совпадает с числом неизвестных. Если матрица системы невырождена, то решение системы существует и единственно. Рассмотрим соответствующую однородную систему L^(k)(a) = 0, k = 0, 1,…,(m-1); aÎS. Эти равенства означают, что многочлен L имеет с учетом кратностей не менее |S| корней, что возможно только при L = 0. Следовательно, однородная система имеет только тривиальное решение, а потому матрица системы невырождена.

Укажем некоторые “явные” формулы для интерполяционных многочленов.

1. Пусть S = {a^[m]}. В этом случае интерполяционный многочлен совпадает с многочленом Тейлора:

2. Пусть S = {a₁, a₂, …,a_p}, то есть кратности всех корней равны 1. Многочлен L в этом случае называется многочленом Лагранжа и строится следующим образом. Положим: L_i = p_S(x)/(x-a_i). Каждое из этих частных представляет собой многочлен степени |S| -1, который обращается в 0 во всех точках спектра, кроме точки a_i, в которой он отличен от нуля. Проверим, что В самом деле, во-первых, эта сумма представляет собой многочлен степени не выше |S|-1. Во-вторых, если положить x = a_k, то все слагаемые под знаком суммы обращаются в 0,за исключением слагаемого с номером i = k, которое равно b_k . Итак, действительно L(a_k) = b_k, что и требовалось.

3. В самом общем случае интерполяционный многочлен можно строить следующим способом. Пусть для каждого i = 1, 2,…, p построен многочлен Тейлора . Положим: 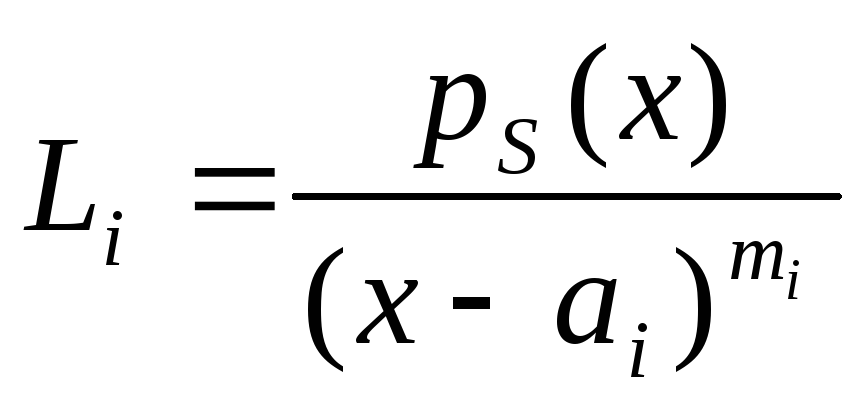. Для каждой рациональной функции R_i = T_i/L_i построим многочлен Тейлора . Тогда: . Доказательство мы оставляем читателю.