
Лекции по АиГ / Alg_09
.docВекторные пространства (продолжение).
Базис подпространства.
Обсудим вопрос о построении базиса подпространства конечномерного пространства V. Поскольку всякое такое пространство изоморфно координатному, можно с самого начала считать, что V = km. Подпространство WÌ km обычно задается либо как линейная оболочка некоторой системы векторов, либо как множество решений однородной системы линейных уравнений.
Базис линейной оболочки системы векторов.
Пусть задана упорядоченная система S = (v1, v2,…, vn) векторов координатного пространства km. Можно предложить правило, позволяющее однозначно выбрать подсистему e Ì S, составляющую базис подпространства <S> Ì km. В дальнейшем будем называть этот базис каноническим.
Правило выбора базисных векторов из системы S.
Вектор v1 входит в (e) тогда и только тогда, когда он ненулевой.
Вектор vp (p = 2, 3,…, n) входит в (e) тогда и только тогда, когда он не является линейной комбинацией предшествующих векторов v1, v2,…, vp-1.
Теорема 1.
Векторы
![]() ,
где 1£j1<…<jr£n,
выбранные в соответствии со сформулированным
правилом, составляют базис (e)
линейной оболочки <S>.
,
где 1£j1<…<jr£n,
выбранные в соответствии со сформулированным
правилом, составляют базис (e)
линейной оболочки <S>.
Прежде чем
доказывать теорему 1 установим ее связь
с приведением матрицы к главному
ступенчатому виду. Образуем матрицу A
Î Matm´n(k),
столбцами которой являются векторы-столбцы
системы S,
взятые в указанном порядке. Приведем
эту матрицу к главному ступенчатому
виду Г и выделим у нее ненулевые строки:
Г =
![]() .
Будем называть BÎ
Matr´n(k)
ненулевой частью ступенчатой матрицы
Г. Напомним, что r =
rkA.
Столбцы матрицы Г образуют систему T
= (u1, u2,…,
un)
из n
векторов пространства km.
.
Будем называть BÎ
Matr´n(k)
ненулевой частью ступенчатой матрицы
Г. Напомним, что r =
rkA.
Столбцы матрицы Г образуют систему T
= (u1, u2,…,
un)
из n
векторов пространства km.
Теорема 2.
Канонический базис f Ì T состоит в точности из главных столбцов матрицы Г. Вектор uiÎf тогда и только тогда, когда viÎe. Размерности подпространств <S> и <T> равны рангу матрицы A. Координаты векторов ui и vi в канонических базисах равны между собой и совпадают со столбцом ci(B) матрицы B.
Доказательство.
Доказательство теорем 1 и 2 будем проводить одновременно. Проверим, прежде всего, что (f) состоит из главных столбцов Г и является базисом <T>. В самом деле, если вектор ui является главным столбцом Г, то все его координаты равны 0, за исключением gqi = 1, которая является главным элементом строки lq(Г). Следовательно, все элементы gqj =0 при j<i и потому вектор ui нельзя представить в виде линейной комбинации предшествующих столбцов матрицы Г. Если же вектор ui не является главным столбцом и gqi ¹ 0, то, обозначая через jq<i номер главного столбца, содержащего единицу в строке с номером q, имеем:
![]() (1).
Это означает, что вектор ui
является линейной комбинацией
предшествующих главных столбцов матрицы
Г. Тем самым показано, что, во-первых,
правило построения канонического базиса
в рассматриваемом случае приводит к
системе главных столбцов ступенчатой
матрицы Г. Во вторых, каждый столбец Г
можно представить в виде линейной
комбинации столбцов системы (f),
а потому (f)
порождает подпространство <T>.
Так как главные столбцы линейно
независимы, то система (f)
– базис подпространства. Из соотношения
(1) вытекает, что ненулевые элементы
столбца ci(Г)
равны координатам вектора ui
в этом базисе. Тем самым установлены
все утверждения теорем 1 и 2, относящиеся
к системе <T>.
(1).
Это означает, что вектор ui
является линейной комбинацией
предшествующих главных столбцов матрицы
Г. Тем самым показано, что, во-первых,
правило построения канонического базиса
в рассматриваемом случае приводит к
системе главных столбцов ступенчатой
матрицы Г. Во вторых, каждый столбец Г
можно представить в виде линейной
комбинации столбцов системы (f),
а потому (f)
порождает подпространство <T>.
Так как главные столбцы линейно
независимы, то система (f)
– базис подпространства. Из соотношения
(1) вытекает, что ненулевые элементы
столбца ci(Г)
равны координатам вектора ui
в этом базисе. Тем самым установлены
все утверждения теорем 1 и 2, относящиеся
к системе <T>.
Напомним теперь, что при приведении к главному ступенчатому виду с помощью элементарных преобразований строк, матрица A умножается на некоторую обратимую матрицу P: Г = PA. Соответствие v « Pv = u является взаимно однозначным между столбцами матриц A и Г и сохраняет их порядок. Кроме того, это соответствие сохраняет линейные операции над векторами и потому определяет изоморфизм подпространств <S> и <T>. Поскольку правило построения канонического базиса сформулировано в общих терминах, этот изоморфизм приводит во взаимно однозначное соответствие системы векторов (e) и (f). Следовательно, все утверждения, доказанные выше для системы <T>, верны и для системы <S>, что и требовалось.
Следствие.
Главный ступенчатый вид матрицы определен однозначно.
Достаточно заметить, что столбцы ненулевой части главной ступенчатой матрицы эквивалентной A равны координатам соответствующих столбцов самой матрицы A в каноническом базисе подпространства <S>, а координаты вектора и канонический базис определены однозначно.
Базис подпространства решений однородной системы.
Каждая однородная
система линейных уравнений Ax
= O
, где AÎMatm´n(k),
определяет подпространство решений
VAÌ
kn.
Для построения базиса этого подпространства
приведем A
к главному ступенчатому виду Г. Пусть
J = (j1<j2<…<jr)
– номера главных столбцов матрицы Г, P
= (p1<p2<…<pn-r)
– номера остальных столбцов, так что
 -
набор главных, а
-
набор главных, а
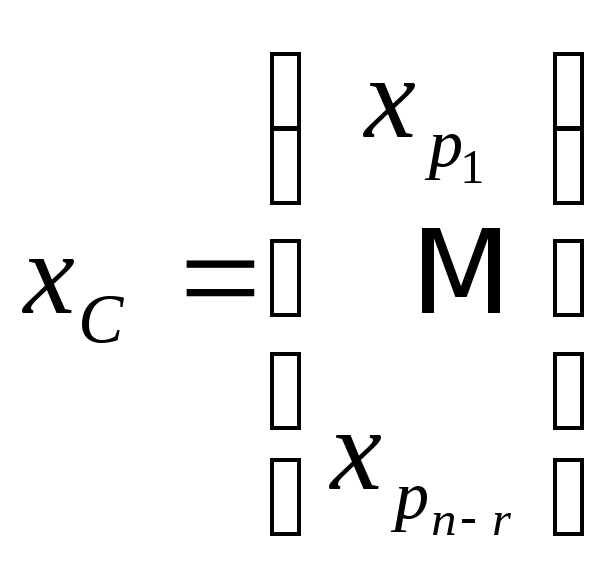 -
набор свободных неизвестных. Здесь r
= rkA.
Как известно, свободные неизвестные
могут принимать любые наперед заданные
значения, а главные неизвестные через
них однозначно выражаются. Введем
матрицу D
размера r´(n-r)
с элементами
-
набор свободных неизвестных. Здесь r
= rkA.
Как известно, свободные неизвестные
могут принимать любые наперед заданные
значения, а главные неизвестные через
них однозначно выражаются. Введем
матрицу D
размера r´(n-r)
с элементами
![]() (напомним, что gab
= 0 при a>r!).
Тогда, очевидно, xГ
= -DxC.
Пусть ei
= ci(En),
где En
– единичная матрица порядка n.
Образуем упорядоченные системы
векторов-столбцов EГ
=(ej,
jÎJ)
и EС
= (ep,
pÎP).
(напомним, что gab
= 0 при a>r!).
Тогда, очевидно, xГ
= -DxC.
Пусть ei
= ci(En),
где En
– единичная матрица порядка n.
Образуем упорядоченные системы
векторов-столбцов EГ
=(ej,
jÎJ)
и EС
= (ep,
pÎP).
Теорема.
DimVA = n-r. Базис этого подпространства составляет набор векторов-столбцов матрицы H =EС - EГD.
Доказательство.
Проверим, что
указанные векторы являются решениями
системы Гx = O,
равносильной первоначальной. Заметим,
что Гeq
= cq(ГЕ)
= cq(Г).
Поэтому ГEС
=
![]() ,
и ГEГD
=
,
и ГEГD
=
![]() (e1,…,
er)D
=
(e1,…,
er)D
=
![]() D
=
D
=
![]() .
Следовательно, ГH
= O,
что и требовалось. Поскольку JÇP
= Æ,
линейная независимость векторов системы
EС
влечет за собой линейную независимость
системы столбцов H.
Наконец, если x
– любое решение системы, то y
=
.
Следовательно, ГH
= O,
что и требовалось. Поскольку JÇP
= Æ,
линейная независимость векторов системы
EС
влечет за собой линейную независимость
системы столбцов H.
Наконец, если x
– любое решение системы, то y
=
![]() также
является решением и
также
является решением и
![]() .
Так как значения свободных неизвестных
определяют решение однозначно, x
= y
и потому система столбцов матрицы H
является порождающей, чем и завершается
доказательство.
.
Так как значения свободных неизвестных
определяют решение однозначно, x
= y
и потому система столбцов матрицы H
является порождающей, чем и завершается
доказательство.
Замечание.
Всякий базис подпространства VA называется фундаментальной системой решений (ФСР). Тот базис, который построен в настоящем параграфе, однозначно определяется матрицей системы. Будем в дальнейшем называть его стандартной ФСР. Матрица, столбцы которой составляют ФСР, называется фундаментальной матрицей. Отметим еще, что если все элементы матрицы системы лежат в поле k, то и стандартная фундаментальная матрица обладает этим свойством.
Способы задания подпространств конечномерного пространства.
В этом разделе мы не приводим доказательств, оставляя их читателю. Любое подпространство координатного m-мерного пространства можно задать и как линейную оболочку некоторой системы векторов и как пространство решений некоторой однородной системы линейных уравнений.
Теорема 1.
Пусть UÌkm задано как пространство решений системы Ax = 0, H - фундаментальная матрица этой системы. Тогда U совпадает с линейной оболочкой <H> столбцов этой матрицы.
Теорема 2
Пусть UÌkm задано как линейная оболочка некоторой системы векторов, которые рассматриваются как столбцы матрицы S. Обозначим через G фундаментальную матрицу системы Sty = 0. Тогда U совпадает с пространством решений системы Gtx = 0.
Теорема 3.
Пусть U и V – два конечномерных подпространства любого векторного пространства W. Тогда: dim(UÇV)+dim(U+V) = dimU+dimV.
В последующих теоремах речь идет об описании суммы (Sum) и пересечения
(Intersection) двух подпространств U и V, если каждое из них задано определенным образом. В теореме 4 U задается как линейная оболочка системы векторов S, а V – как линейная оболочка системы T. Каждую из этих систем можно рассматривать как матрицу из векторов-столбцов.
Теорема 4S.
Подпространство U+V совпадает с линейной оболочкой системы SÈT.
Теорема 4I.
Для составной
матрицы (S|T)
рассмотрим систему линейных уравнений
![]() .
Пусть
.
Пусть
![]() - фундаментальная матрица этой системы.
Тогда линейная оболочка <SHS>
или, что то же, <THT>
совпадает с подпространством UÇV.
- фундаментальная матрица этой системы.
Тогда линейная оболочка <SHS>
или, что то же, <THT>
совпадает с подпространством UÇV.
В теореме 5 считаем, что U задано как пространство решений системы Ax = 0, а V – как пространство решений системы Bx = 0.
Теорема 5S.
Рассмотрим систему
линейных уравнений
![]() .
Пусть
.
Пусть![]() фундаментальная матрица этой системы.
Тогда система линейных уравнений
фундаментальная матрица этой системы.
Тогда система линейных уравнений
![]() или, что то же,
или, что то же,
![]() задает подпространство U+V.
задает подпространство U+V.
Теорема 5I
Составная система
![]() задает подпространство UÇV.
задает подпространство UÇV.
В теореме 6 считаем, что U задано как линейная оболочка системы векторов S, а V – как пространство решений системы Bx = 0.
Теорема 6S.
Будем рассматривать S как матрицу из векторов-столбцов. Пусть H - фундментальная матрица системы Bx = 0. Линейная оболочка столбцов составной матрицы (S|H) совпадает с подпространством U+V.
Теорема 6I.
Пусть G - фундаментальная матрица системы (BA)y = 0. Линейная оболочка столбцов матрицы AG совпадает с пересечением UÇV.
Замена базиса.
Пусть в n-мерном
пространстве V
заданы 2 базиса e =
(e1,…, en)
– “старый” базис и
![]() - “новый” базис. Каждый вектор нового
базиса можно разложить по старому
базису:
- “новый” базис. Каждый вектор нового
базиса можно разложить по старому
базису:
![]() .
Числа aij
задают квадратную матрицу A
порядка n,
называемую матрицей
перехода к новому базису.
Можно записать:
.
Числа aij
задают квадратную матрицу A
порядка n,
называемую матрицей
перехода к новому базису.
Можно записать:
![]() ,
если рассматривать базисы как матрицы
с 1 строкой. Отметим, что матрица A
невырождена, так как обратная к ней
матрица является матрицей перехода от
нового базиса к старому:
,
если рассматривать базисы как матрицы
с 1 строкой. Отметим, что матрица A
невырождена, так как обратная к ней
матрица является матрицей перехода от
нового базиса к старому:
![]() .
.
Теорема.
Координаты вектора v в новом и старом базисах связаны соотношением:
![]() .
.
Доказательство.
Имеем:
![]() .
Поскольку координаты вектора определены
однозначно, отсюда и вытекает доказываемое
равенство.
.
Поскольку координаты вектора определены
однозначно, отсюда и вытекает доказываемое
равенство.
Замечание.
Очевидно, что
![]() .
.
