1. Статическая часть расчета

Учитывая особенность металлических конструкций (распределение температуры по их сечению принимается равномерным), для них можно, не определяя кривую снижения несущей способности, сразу вычислить критическую температуру в сечении, вызывающую потерю несущей способности.

Критическая температура определяется в зависимости от коэффициента , учитывающего снижение несущей способности конструкции под действием высокой температуры, который вычисляют:

- для изгибаемых элементов с учетом развития пластических деформаций:

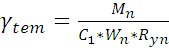, (1)

где M_n – изгибающий момент от нормативной нагрузки, Н*м ;

R_yn – нормативное сопротивление по пределу текучести, Па ;

W_n – момент сопротивления сечения, м3 ;

С₁ – коэффициент, учитывающий развитие пластических деформаций.

Величину коэффициента в зависимости от вида конструкции принимают :

для двутавров и швеллеров С₁=1,17 ;

для труб С₁=1,25 ;

для прямоугольного сечения С₁=1,5 ;

- для центрального растяжения:

, (2)

где N_n – нормативная (рабочая) нагрузка, Н ;

_А- площадь поперечного сечения, м2 ;

- для внецентренного растяжения:

, (3)

где е – эксцентриситет, м.

Сжатые элементы утрачивают несущую способность в результате потери прочности или за счет устойчивости.

Коэффициент снижения несущей способности по потери прочности определяют по формулам соответственно для центрального и внецентренного растяжения.

Вычислив коэффициент загружения конструкции , по графикам или по эмпирическим формулам определяют критическую температуру:

при

, (4)

при

, (5)

Кроме этого, для сжатых элементов по потери устойчивости, можно определить критическую температуру, используя график зависимости критической разности краевых деформаций ползучести от критической температуры и степени загружения . Этот график позволяет определить критическую температуру как для центрально-сжатых, так и внецентренно- сжатых стержней. При этом для центрально-сжатых стержней и находиться по формулам:

, (6)

где ; .

В случае внецентренного сжатия :

, (7)

где ; ; – гибкость стержня; – расчетная длина, м; – длина стержня, м; - коэффициент, зависящий от способа закрепления стержня; Е – модуль упругости стали, Па.

2. Теплотехническая часть расчета

Как известно, металл обладает огромным коэффициентом температуро-проводности, за счет чего выравнивание температуры по его толщине происходит весьма быстро. Это дает возможность принять равномерное распределение температуры. В этом случае можно утверждать, что количество тепла, поглощенное нагреваемой конструкцией за время Δτ через обогреваемую поверхность равно увеличению его теплосодержания, т.е.

, (8)

где α – коэффициент теплоотдачи, Вт/(м2*°С);

t_В – температура по стандартной кривой, °С;

t_cm – температура стержня, °С;

S_cm – обогреваемая поверхность стержня, м2;

Δτ – время, с;

С_cm – начальный коэффициент теплоемкости стали, Дж/(кг*°C);

D – коэффициент изменения теплоемкости стали при нагреве;

ρ_cm – плотность стали, кг/м3;

V – объем металла стержня, м3;

t_cm,Δτ – температура стержня через расчетный интервал времени.

Заменив ; ,где u - обогреваемый периметр стержня, м; А – площадь поперечного сечения, м² ; l- длина стержня, м, и решая уравнение (8) получим:

. (9)

Эта формула является алгоритмом для расчета температуры не защищенных металлических конструкций. Как следует из уравнения, температура конструкций в процессе нагрева зависит только от одного параметра – приведенной толщины металла tred . Приведенная толщина металла дает возможность привести стержни, имеющие любую конфигурацию поперечного сечения, к простой пластине. Значение приведенной толщины в общем случае определяется как отношение площади поперечного сечения к обогреваемому его периметру, т.е.

, (10)

где u – периметр рекомендуется определять:

- для двутавра и швеллера при обогреве с четырех сторон:

, (11)

где - высота сечения элемента; - ширина сечения (полки); - толщина стенки;

- для уголка:

. (12)

Для трубы приведенную толщину рекомендуется вычислять по формуле:

, (13)

где - соответственно наружный диаметр и толщина стенки трубы по сортаменту (приложение 2).

Используя алгоритм расчета, можно составить монограмму, с помощью которой можно определить температуру не защищенных конструкций любых сечений (приложение 5).

Определив критическую температуру, при которой наступает потеря несущей способности конструкции, и используя график зависимости температуры от времени и приведенной толщины металла, вычисляют время нагрева до наступления критической температуры, т.е. фактический предел огнестойкости конструкции.