1. Расчет температур в сплошных плоских конструкций

Нестационарное температурное поле, возникающее в полуограниченном теле от воздействия "стандартного пожара" рассчитывается по формуле:

, (24)

где у - расстояние по нормали от обогреваемой поверхности до расчетной точки тела, м,

Расчетная формула (24) может быть использована для определения температуры в плоских конструкциях конечной толщины. Поэтому данная формула является основной для расчетов температуры плит, панелей, настилов, перекрытий. Taк, формула для расчета температуры арматурных стержней, находящихся на расстоянии у=а₁ от обогреваемой поверхности имеет вид:

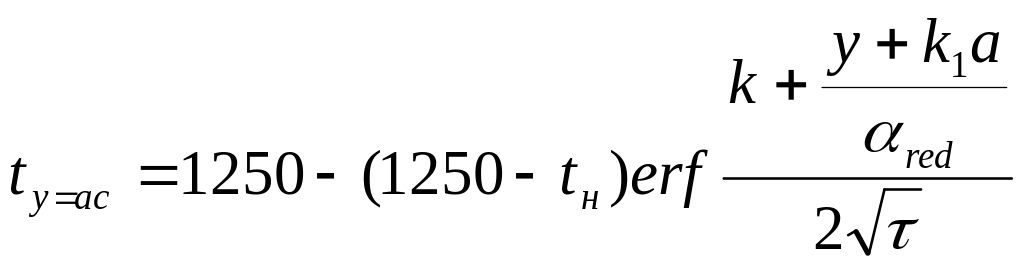, (25)

где у - расстояние от обогреваемой поверхности до края арматуры, м;

k₁ - коэффициент, для бетонов с ρ= 2000 кг/м³ равен 0,5.

Поскольку предел огнестойкости свободно опертых элементов зависит от прогрева растянутой рабочей арма­туры до критической температуры t_s,сr , зная ее величину, можно найти иx предел огнестойкости. Порядок опре­деления t _с,cr (см. статический расчет).

Затем используя формулу (24) при t_y,τ= t_s,сr ,находится аргумент x(А) в зависимости от значения функции Гаусса (Крампа):

, (26)

.

Предел огнестойкости τ = П_ф будет равен:

,(27)

где τ= П_ф,с.

Для определения температур в плоских конструкциях при двустороннем обогреве решают задачу о прогреве неограниченной пластины при симметричных граничных условиях.

Это решение имеет вид [11]

, (28)

где

;

x - расстояние от центра до расчетной точки по толщине пластины, м;

в - толщина пластины, м;

- критерий Фурье;

τ –время,с.

Таким образом, формулу (28) можно преобразовать к виду:

. (29)

Выражения в квадратных скобках формул (28) и (29) представляют относительную избыточную температуру θ, которую можно определить по графику в зависимости от F₀ и ξ (приложение 10). Тогда необходимую температуру находят по формуле:

. (30)

При расчетах огнестойкости (колонны, балки, ригели) необходимо найти температуру в середине толщины пластины, т.е. при x =0

,(31)

где θ_ц - относительная температура, определяемая по данным приложения 11 в зависимости от F₀/4.

2. Температура арматуры в стержневых конструкциях.

При прогреве балок, колонн, ферм и других стержневых элементов, обогреваемых в условиях пожара с трех или четырех граней боковых поверхностей, имеет место двухмерное температурное поле. Расчет температур в этих случаях может быть выполнен с достаточной точностью при помощи известного в теории теплопроводности соотношения относительных температур:

(32)

где t_в – по стандартной кривой (2.1);

t_x,y,τ – температура двухмерного поля, ⁰ C;

t_x, t_y – температура одномерных полей, ⁰С.

Из соотношения (32) находят:

(33)

Согласно [10] температуру в сечениях железобетонных элементов можно определять по графикам прогрева, полученных экспериментальным путем (приложение 18).

3. Расчет слоев бетона, прогретых до заданных температур.

При огневом воздействии сечение конструкций прогревается неравномерно. Поэтому в каждом слое (точке) сечения температура имеет определенное значение. Если в одном из этих слоев (точек) расположен несущий элемент, воспринимающий все сжимающие или растягивающие усилия, то температура его будет определять величину несущей способности всей конструкции. В тот момент, когда несущая способность этой конструкции снизится до величины рабочей нагрузки и наступит ее предел огнестойкости, температура является критической.

Такими несущими элементами являются растянутая арматура в изгибаемых железобетонных конструкциях. Предел огнестойкости этих конструкций рассчитывается путем вычисления времени прогрева их несущих элементов до критической температуры.

Таким образом, понятие критической температуры относится не к материалу конструкции, а к ее несущему элементу. Нельзя, например, в этом смысле говорить о критической температуре бетона, так как этот материал расположен по всему сечению в железобетонной конструкции, прогревается неравномерно и не имеет поэтому какой-то определенной температуры нагрева.

Иногда с целью упрощения расчета все же применяют термин «критическая температура» и к бетону.

Так, например, называют критической температуру на границе ядра сечения железобетонных колонн, которая условно отделяет бетон с нулевой прочностью от бетона с начальной прочностью. Однако в этом случае критическая температура имеет другой смысл, связанный с ограничением какой-то площади поперечного сечения, и является скорее приемом для упрощения расчета [8]. Этим приемом пользуются при расчете огнестойкости, например, колонн, статически не определимых изгибаемых конструкций. Иначе говоря, необходимо определять толщину бетонных слоев, прогревающихся до заданных критических температур. Прочность бетона в этих слоях считается равной нулю, а в оставшемся сечении (ядре) – нормативной.

Эта задача является обратной рассмотренным выше и решается на основе тех же уравнений и зависимостей.

Толщина слоя у плоской конструкции, прогретого выше t_cτ (изотерма t_cτ- граница слоя) определяет по уравнению (34):

, (34)

где x- аргумент функции Гаусса (Крампе) erf x (A) определяется:

, (35)

где t_в,cr - критическая, расчетная температура бетона:

• для тяжелого бетона на гранитном щебне-650°С;

• для тяжелого бетона на известняковом щебне -750°С.

При обогреве конструкции с четырех сторон:

(36)

где ξ_x - определяют по графику (приложение 10) в зависимости от величин θ_x и F_0x:

_{, (37)}

- определяется по формуле(31);

θ_ц принимают по данным приложения 11 в зависимости от F_ox/4:

, (38)

,

где ξ_y - находят из графика (приложение 10) в зависимости от θ_ц и F_oy

, (39)

t_x=0,τ =1250-(1250-t_н) θ_ц определяется по формуле (31), θ_ц - принимают по данным приложения 11 в зависимости от F_oуx/4:

.

Зная величину , и решая это неравенство относительно δ_tem,y , получаем уравнение (38).

В том случае, когда прямоугольное сечение обогревается с трех сторон толщину слоя δ_tem,y находят по формуле:

, (40)

где величина х является аргументом функции ошибок Гаусса

(приложение 9) , рассчитанной по формуле:

. (41)

Температуру t_x=0,τ определяют по формуле (31).

Координату δ_tem,x у необогреваемой грани сечения находят по формуле (36) с использованием выражения (37), в котором t_y=0,τ нужно заменить температурой t_y=h , определяемой по формуле(24) при y=h.

Таким образом:

- при четырехстороннем обогреве:

, ;

-при трехстороннем обогреве:

, .