4.2. Методичні засоби забезпечення єдності вимірювань

Важливою умовою забезпечення єдності вимірювань є відповідність (у межах установленої точності) розмірів величин, що вимірюються, розмірам фізичних одиниць, відтворюваних державними еталонами та зразковими засобами вимірювань. Для досягнення єдності вимірювань необхідно мати єдину уніфіковану методику вимірювань, що встановлює єдиний метод, однакову кількість вимірювань, однакові вимоги до умов вимірювань, до кваліфікації оператора тощо.

Коротко про єдність вимірювань можна сказати, що це характеристика якості вимірювань. У поняття якості вимірювання входять результати вимірювань, виражені в узаконених одиницях, розміри яких в установлених межах дорівнюють розмірам відтворених одиниць, а похибки результатів вимірювань відомі із заданою вірогідністю і не виходять за встановлені межі.

Поняття "єдність вимірювань" охоплює такі важливі напрями метрології, як уніфікація одиниць та визнання їх законними; розроблення системи відтворення одиниць та передачі їх розмірів робочим засобам вимірювань. Створення державних еталонів, що відтворюють одиниці з найвищою точністю, і розроблення методів передачі розмірів одиниць із установленою точністю є запорукою рівності розмірів одиниць при використанні робочих засобів вимірювання. Відповідність розмірів одиниць, що відтворюються державними чи міждержавними еталонами або еталонами інших країн, – основа єдності вимірювань на міждержавному рівні або на рівні декількох країн.

Таке визначення охоплює похибку вимірювань, яка складається з похибок засобів вимірювання та методу вимірювання і значно залежить від методики вимірів (умови, кількості вимірів тощо). Похибка вимірювань не повинна перевищувати установлену межу. Не встановивши межу похибки вимірювань, що випливає з конкретної вимірювальної задачі, не можна розв’язати питання про правильний вибір засобів вимірювання, дати правильну оцінку результатів вимірювання, що виконувалися у різних місцях, тобто важко дотриматись єдності вимірювань.

Для забезпечення єдності вимірювань розробляються загальні вимоги до засобів вимірювання, що випускаються (за точністю, діапазоном вимірювань). Таким чином, єдність вимірювань тісно пов'язана з їх точністю. Вона повинна витримуватись при будь–якій точності вимірювань, необхідній у практиці.

Забезпеченням єдності вимірювань займаються метрологічні та інші служби, діяльність яких націлена на досягнення єдності вимірювань при необхідній точності і регламентується стандартами й іншими нормативно–технічними документами державної системи забезпечення єдності вимірювань.

Лекція №5.

обробка результатів вимірювань

5.1. Випадкові величини та характеристики їх розподілу.

5.2. Статистична обробка результатів.

Література: [1], С.7-13,19-21; [2], С.433-442.

5.1. Випадкові величини та характеристики їх розподілу

Випадковою називають величину ‚ яка внаслідок досліду може набувати різних значень x‚ що лежать в інтервалі залежно від випадкового результату досліду. Ймовірнісні властивості випадкової величини описують за допомогою функції розподілу F(x)‚ яка за ознакою є зростаючою до одиниці‚ тобто F( -) = 0 і F()= 1 ( рис. 1).

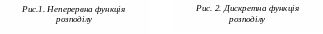
Функцією розподілу називають імовірність того‚ що випадкова величина X у результаті досліду набуде значення‚ менше ніж x‚ де x- будь-яке дійсне число

. (4)

Якщо випадкова величина X може набувати лише дискретних значень то розподіл називають дискретним. Функція розподілу в цьому разі дискретна‚ вона зростає східчасто за тих значень x‚ які є можливими значеннями випадкової величини X ( рис. 2).

Неперервна випадкова величина – це така величина‚ яка може набувати будь-яких значень в одному або кількох заданих інтервалах‚ або областях площини‚ або простору. Ці значення утворюють нескінченну множину‚ яку називають континіумом.

Для неперервної величини існує перша похідна від функції її розподілу‚ яка називається щільністю розподілу ймовірностей

. (5)

За допомогою функції (x) дістаємо ймовірність виявлення величини X у нескінченно малому інтервалі

‚ (6)

а ймовірність виявлення тієї самої величини в скінченному інтервалі

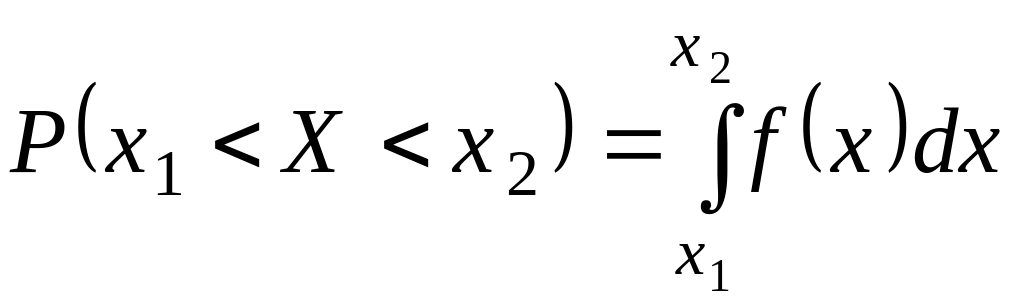. (7)

Імовірність того‚ що величина X лежатиме в інтервалі ‚ напевне дорівнює одиниці. Звідси дістаємо умову нормування

. (8)

При описі неперервного розподілу часто використовують так звані квантилі. Квантилем‚ що відповідає заданому рівню ймовірності p‚ називають таке значення x=x_p ‚ при якому функція розподілу набуває значення‚ що дорівнює p . Деякі квантилі мають особливу назву. Так‚ медіаною розподілу називається квантиль‚ що відповідає значенню p=1/2. Квантилі‚ що відповідають значенням p=1/4 і p=3/4‚ називають відповідно нижнім та верхнім квантилями.

Мода неперервного розподілу – значення аргументу‚ при якому щільність розподілу досягає максимуму (тобто найімовірніше її значення).

У деяких задачах знати функцію розподілу чи щільність імовірності необов’язково і досить визначити певні числові характеристики. Щоб обґрунтувати запровадження цих характеристик‚ потрібно повернутися до статистичного означення ймовірності.

Середнє арифметичне значення випадкової величини X за умови‚ що остання набуває n₁ разів значення x₁, n₂ - значення x₂ і т.д.

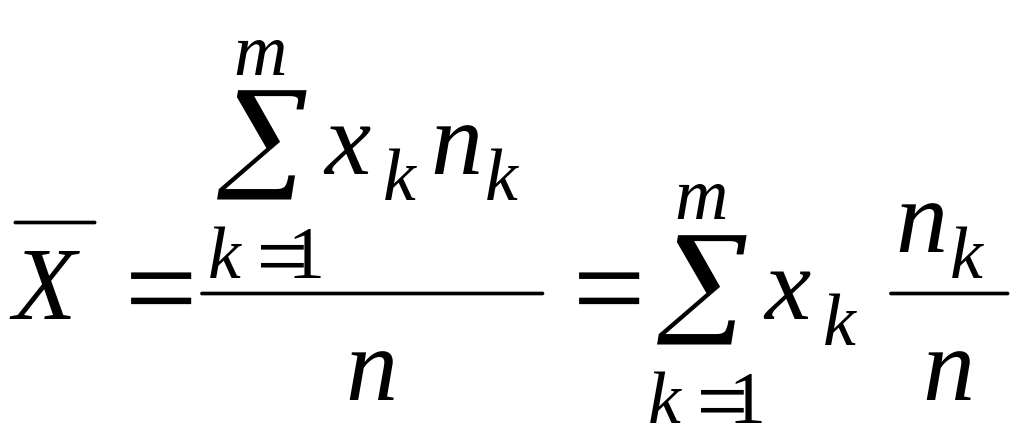. (9)

Якщо емпіричні частоти замінити ймовірностями p₁ , p₂ , . , p_n , то середньому арифметичному значенню може бути відповідною теоретична характеристика випадкової величини

‚ (10)

названа математичним сподіванням випадкової величини X. Переходячи до неперервного розподілу‚ маємо

. (11)

Згідно із законом великих чисел зі збільшенням кількості випробувань середнє емпіричне значення Х наближається до математичного сподівання М(Х).

Якщо розглянути довільну невипадкову функцію випадкової величини Х‚ то математичне сподівання функції буде мати вигляд

. (12)

Зокрема‚ якщо ‚ то отримуємо вираз для початкового моменту n-го розряду випадкової величини Х

. (13)

Момент першого порядку випадкової величини є її математичне сподівання.

Початковий момент другого порядку

. (14)

Квадратний корінь із ₂ називається середнім квадратичним значенням випадкової величини

‚ (15)

₁ і ₂ дають лише середнє значення випадкової величини і не відображають характеру розкиду навколо середнього значення.

Для оцінювання розкиду випадкової величини біля її математичного сподівання вводиться поняття дисперсії_{. .} Дисперсією дискретної випадкової величини Х‚ можливі значення якої з’являються з імовірностями ‚ називається сума додатків квадратів різниць можливих значень випадкової величини та її математичного сподівання на відповідні цим можливим значенням імовірності

. (16)

Крім того‚ D(X) можна тлумачити як математичне сподівання квадрата відхилень можливих значень випадкової величини від її математичного сподівання

. (17)

Для неперервно розподіленої випадкової величини

. (18)

Додатне значення квадратного кореня з дисперсії називають середнім квадратичним відхиленням, або стандартом,

. (19)

Дисперсія і стандарт – це міра розсіяння випадкової величини навколо середнього значення.

Коефіцієнт варіації – широко використовувана характеристика випадкової величини

. (20)

Із-поміж теоретичних розподілів випадкових величин велике значення має нормальний розподіл .

Якщо розподіл випадкової величини підпорядковується певному закону‚ щільністю

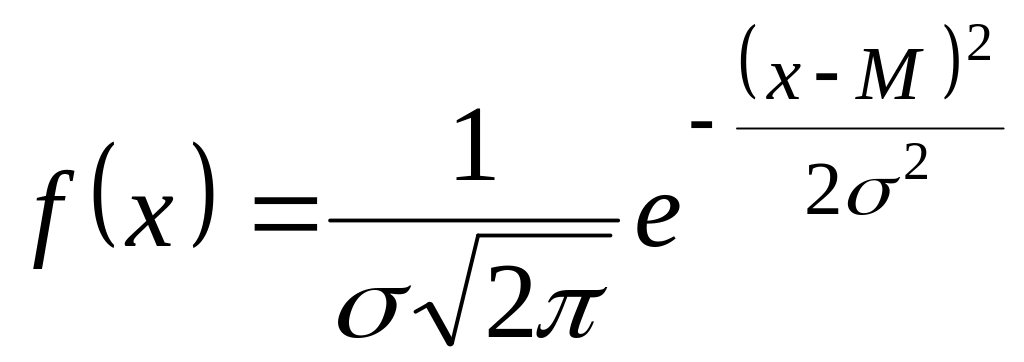‚ (21)

то такий розподіл називають нормальним і він вважається основою математичної статистики.

Щільність імовірності задовольняє умову нормування‚ а параметри М і  – відповідно математичне сподівання випадкової величини X та її стандарт.

Для щільності ймовірності нормального розподілу (рис. 1.3) чим більший стандарт  ‚ тим більший розкид випадкової величини навколо її середнього значення (математичне сподівання). Крива нормального розподілу симетрична відносно середнього значення.

Приблизно 2/3 усіх спостережень лежить у площі‚ що відсікається перпендикулярами до осі ОХ (М± ). При великому обсязі вибірки приблизно 90 % усіх спостережень лежить між -1‚64 і +1‚64. Границі 0‚675 та +0‚675 називають імовірнісними відхиленнями ‚ в цьому інтервалі знаходиться приблизно 50 % усіх спостережень.

Для нормального розподілу середнє значення‚ мода та медіана збігаються.

У багатьох випадках дослідні дані свідчать про значне відхилення випадкової величини від середнього значення. З огляду на це, теоретичні закони розподілу широко застосовуються для опису експериментальних даних і в практиці ймовірних розрахунків.

Методи опису й аналізу експериментальних даних є предметом математичної статистики. На відміну від теорії ймовірності‚ яка оперує характеристиками теоретичного розподілу випадкових величин‚ математична статистика має справу з правилами одержання‚ обробки і зображення емпіричних розподілів. Основне завдання статистики полягає у визначенні теоретичного розподілу за відомим розподілом емпіричних частот. Таку задачу зводять до наближеного знаходження невідомих параметрів розподілу та до оцінювання надійності одержаних значень.

Рис.3. Щільність нормального розподілу

Якщо внаслідок n вимірювань випадкової величини X одержано послідовність значень ‚ то первинна обробка полягає в групуванні знайдених значень за достатньо малими інтервалами‚ обчисленні середніх відносних частот для кожного інтервалу й графічному зображенні результатів у вигляді гістограми‚ полігону чи кумулятивної кривої (рис.4).

Р ис..4. а) Статистична функція розподілу, б) гістограма варіаційного ряду, в) полігон варіаційного ряду

Гістограми та полігон відповідають кривій теоретичної щільності ймовірності‚ а кумулятивна крива (статистична функція розподілу) – кривій теоретичної функції розподілу.

Основними характеристиками емпіричного розподілу є середнє арифметичне значення

(22)

і середнє квадратичне відхилення для генеральної сукупності ² ‚ для вибірки - S²

. (23)

Вибірковою сукупністю (вибіркою) називається відібрана для вивчення частина об’єктів. Генеральною сукупністю називається вихідна сукупність об’єктів‚ із яких робиться вибірка.

Відповідні параметри теоретичного розподілу - математичне сподівання M(X) та дисперсія D(X). Проте характеристики емпіричного розподілу - випадкові величини. Зробивши дві серії спостережень над випадковою величиною X‚ можна в загальному випадку дістати різні значення середніх величин і середніх квадратичних відхилень. Чим більша кількість дослідів‚ тим точніше можна оцінити параметри емпіричного розподілу.

Відношення

(24)

називають коефіцієнтом мінливості (коефіцієнт варіації для теоретичного розподілу).

Для опису емпіричних розподілів застосовують й інші безрозмірні параметри‚ зокрема коефіцієнти асиметрії

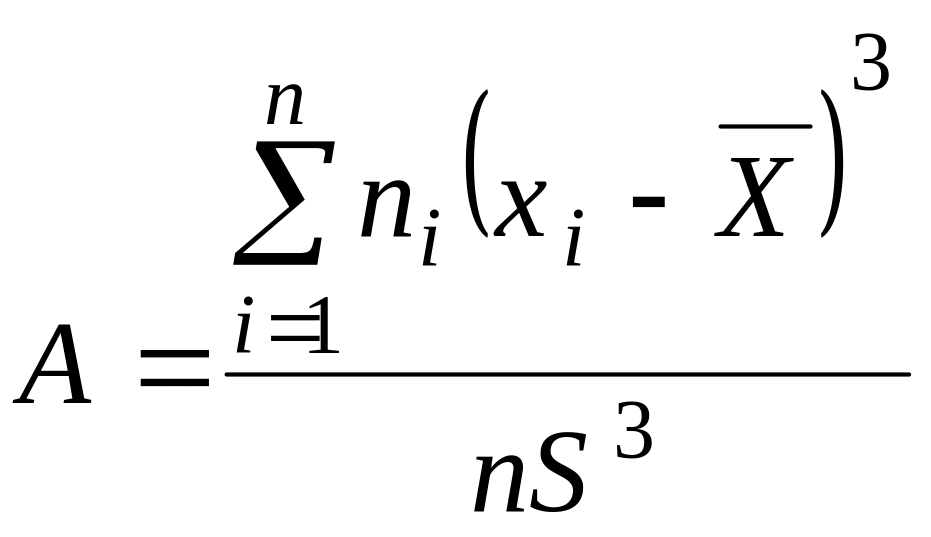(25)

та ексцесу

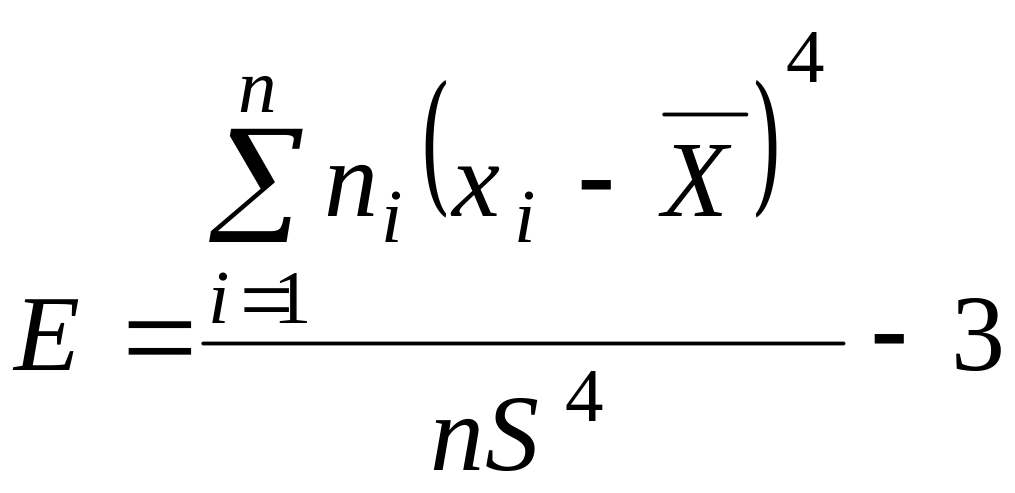. (26)