Қоғамдық денсаулық сақтау және информатика кафедрасы

АҚПАРАТТЫ-ДИДАКТИКАЛЫҚ ҚҰРАЛ

Пән: «Биостатистика»

Бірінші сабақ

Статистикалық жиынтық. Бас жиынтық

Статистикалық жиынтық деп – белгілі сапалық және сандық қасиеттермен берілетін барлық қарастырып отырған объектілер жиынын айтамыз.

Барлық объектілерінен құрылатын жиынтықты жалпы жиынтық дейміз.

Бас жиынтықтың объектілер санын жиынтық көлемі дейміз және «N» әрпімен белгілейміз.

Бас жиынтықтан іріктеп алынған объектілер – іріктелген немесе таңдамалы жиынтық деп аталады және оның көлемі «n» белгіленеді.

Варианттардан және олардың жиілігінен не салыстырмалы жиілігінен құралатын қатарды статистикалық дискреттік қатар дейміз.

Зерттейтін белгі (х)

Белгі жиілігі (m)

(х) =m

∑ m= n Жиіліктің қосындысытаңдаманың көлеміне тең. Жиіліктің (m) таңдама көлеміне (n) қарым-қатынасы салыстырмалы жиілік дейміз (P).

P= m/ n

Интервал мәндерінен және олардың жиілігінен не салыстырмалы жиілігінен құралатын қатарды интервалдық дискреттік қатар дейміз.

Полигон және гистограмма.

Статистикалық тарату графика жүзінде полигон және гистограмма арқылы көрсетуге болады. Варианттың саны шамалы болғанда полигонды қолданады, ал вариантардың саны көп болса және белгілің таралуы үздіксіз болса гистограмманы қолданады. О_х осі бойынша варианттардың деректерін орналастырады, ал О_у осі бойынша жиіліктің не салыстырмалы жиіліктің мәліметтерін орналастырады.

0,4

0,3

0,2

0,1

1 2 3 4 5 5 10 15 20 25 30 40

П о л и г о н г и с т о г р а м м а

Бас жиынтық сипаттамасы.

Таңдамлы орташаны есептеу:

=

х – зерттейтін белгі (оның сандық мәні)

n – таңдаудың көлемі

m – сандық белгінің жиілігі

Х1	19	20	21	22	23
m1	2	1	6	8	2

= ∑m= n=19

Х = = = ; Х=21,3

Бас жиынтықтың сандық белгісін таңдамалы орташа айналасындағы бытыраңқылығын анықтау үшін бас дисперсия деген сипаттаманы қолдау қажет

1. Бас дисперсия Д_r

Д_r =

2. Таңдамалы жиынтықтың сандық белгісінің таңдамалы орташа айналасындағы бытыраңқылығын анықтау үшін таңдамалы дисперсия деген сипаттаманы қарау қажет Д _b.

Д _b – таңдамалы дисперсия

Д_b= Х_b=21,3

Д_b= = Д_b= 0,55

Орташа квадраттық ауытқу белгінің әр түрлілігін сипаттайды.

σ - орташа квадраттық ауытқу

σ_r =√ Д_r (жалпы квадраттық ауытқу)

σ_b =√ Д_b (таңдамалы квадратттық ауытқу).

Есептің жалғасы

Таңдамалы квадраттық ауытқу

σ_b =

Сенім аралық статистикалық қателік. Белгісіз мәләметті табатын ықтималды – сенімділік ықтималы – дейміз.

Сенімділік ықтималы – γ

(γ) тең 0,9; 0,95; 0,99; 0,999

Есептің жалғасы

γ ═

t – кесте бойынша табамыз = 2,10

Сенімдік аралық:

21,3- 0,36= 21,60

21,3+ 0,36= 20,9

Е С Е П Т Е Р:

1.Таралу кестесі

х1	1	2	3	4	5	6
m	10	20	15	10	12	5
р

Есептеу қажет:

1. Таңдамалы орташаны

2. Таңдамалы дисперсияны

3. Орташа квадраттық ауытқуды

4. Стандарттық қатені

5. Сенімдік шегін

6. Салыстырмалы жиілік

7. Полигон арқылы бейнелеу

2. 8 жасар ер баланың бойы. (см)

х1	115	116	117	118	119	120	121
m	1	2	6	10	15	20	30
р

Есептеу қажет:

1. Таңдамалы орташаны

2. Таңдамалы дисперсияны

3. Орташа квадраттық ауытқуды

4. Стандарттық қатені

5. Сенімдік шегін

6. Салыстырмалы жиілік

7. Полигон арқылы бейнелеу

3. Перезенттердің салмағы (кг)

х1 (см)	1,900	2,200	2,500	2,900	3,00	3,500	4,000	4,500
m	1	2	5	14	18	20	8	5
р

Есептеу қажет:

1. Таңдамалы орташаны

2. Таңдамалы дисперсияны

3. Орташа квадраттық ауытқуды

4. Стандарттық қатені

5. Сенімдік шегін

6. Салыстырмалы жиілік

7. Полигон арқылы бейнелеу

Әдебиеттер:

1. И.И.Баврин 279 бет

2. О.М.Жолымбаев. Жоғарғы математика – 279 б.

Сұрақтар

1. Бас жиынтық

2. Таңдамалы жиынтық

3. Статистикалық дискреттік қатар

4. Интервалдық дискреттік қатар

5. Полигон, гистограмма

6. Таңдамалы орташа

7. Таңдамалы дисперсия

8. Орташа квадраттық ауытқу

Т Е С Т Т Е Р

1. Бас және таңдамалы жиынтық қандай жиынтықты құрайды?

1. Статистикалық жиынтық

2. Өлшем жиынтық

3. Таралу жиынтық

4. Интервалдық жиынтық

5. Эмпириалдық жиынтық

2. Жиынтықтағы объекті сандарын қалай атаймыз?

1. Белгі

2. Вариант

3. Жиілік

4. Көлемі

5. Дисперсия

3. Берілген формула ∑ m= n нені анықтайды? ?

1. Салыстырмалы шаманы

2. Таңдама көлемін

3. Орташа таңдаманы

4. Орташа дисперсияны

5. Квадраттық ауытқу

4. При небольшом количестве вариант какое графическое изображение используют?

1. Секторную

2. Столбиковую

3. Полигон

4. Гистограмму

5. Внутристолбиковую

5. Таңдама дискретті вариациялық қатар берілген:

Х1	1	2	3	4
m	20	15	10	5

Таңдама көлемін табамыз:

1. 20

2. 25

3. 5

4. 10

5. 50

6. Егер вариантты жиіліктің көбейтілген қосындысы 520 тең , таңдама көлемі n =27.

Орташа таңдама нешеге тең?

1. 2,3

2. 22,3

3. 19,2

4. 18,5

5. 21,3

7. Таңдама орташа дисперсия σ = 0,57. Орташа квадраттық ауытқу нешеге тең?

1. 0,61

2. 0,32

3. 0,33

4. 0,75

5. 0,12

8. Бас дисперсия нені сипаттайды?

1. Белгінің әртүрлілігі

2. Белгінің бытыраңқылығы

3. Белгінің жиілігі

4. Белгінің саны

5. Белгінің көлемі

9. Берілген σ_b =√ Д_b формула арқылы нені есептейміз?

1. Квадраттық орташа ауытқуы

2. Бас дисперсияны

3. Таңдама дисперсияны

4. Таңдама орташаны

5. Бас орташаны

10. Белгісіз мәліметті табатын ықтималды қалай атаймыз?

1. Жиынтық

2. Орташа орта

3. Бас дисперсия

4. Жиілік

5. Сенімдік ықтимал

Екінші сабақ

Екі бас жиынтықты Х пен У және таңдама жиынтық нәтижелері бойынша Н₀ жорамалды тексеруін талап етеді.

Жорамалды тексеру 5 кезеңнен құралады:

1. Зерделеуде нольдік не алтернативті жорамалдарды

2. Таңдамадан қажетті мәліметтерді алу

3. Н₀ жауапты статикалық критерияны есептеу

4. Статистикалық критерия мәліметтерін, тарау ықтимал мәліметтермен салыстыру

5. Айқындық (Р) деңгейін және нәтижесін дәлелдеу

Н₀ – жорамалды, орташа дисперсия және орташа таңдаманы анықтау қажет.

Келесі статистикалық критерийді анықтаймыз «Z»

Z

N_y –таңдама көлемі

1 курс студенттері

X1	165	168	170	175	178	180
m	2	3	3	7	9	6

2 курс студенттері

Y1	165	168	170	175	178	180
m	1	5	7	6	5	6

Болжау деңгейі Р=0,05 І, ІІ курс студенттерінің орташа мәнінің арасында айқын айырмашылығын анықта:

1. Таңдама орташаны анықтау:

Х₁=175

II.Эксперименттік не статистикалық критерийді анықтау.

Z=

ІІІ. Критерии Z_кр анықтаймыз

Z_кр

ІV. Z_экс , Z_кр мәндерін салыстыру

Егер, Z_экс > Z_кр болса, нолдік жорамалды теріске шығару керек.

Егер, Z_экс < Z_кр болса, нолдік болжамды қабылдайды.

Біздің мысал есебіміз бойынша:

Z_экс=3,3 Z_экс > Z_кр жоғары,сол себептен нөлдік жорамалды теріс дейміз

Z_кр =1,99

Е С Е П Т Е Р

1 есеп

Х	50	52	54	55	59
m	1	4	7	8	10

У1	50	52	54	55	59
m	-	3	8	12	13

Болжау деңгейі P=0,05 . Екі перезентханада туған перезенттердің бойларының арасындағы айқын айырмашылықты анықта:

1. Таңдама орташа

2. таңдама дисперсия

3. эксперименталдық (бақылау) критерий Z_экс

4. қауіпті критерий Z_кр

5. айқын айырмашылықты анықтау

2 есеп

Х1	68	78	80	90	95
m	5	7	10	15	3

Xy	68	78	80	90	95
n	3	8	15	12	2

Болжау деңгейі P=0,05 . Екі топқа функциялық жаттығудан кейін 1 минут жүрек соғысының айқын айырмашылығын анықта

1. Таңдама орташа

2. таңдама дисперсия

3. эксперименталдық (бақылау) критерий Z_экс

4. қауіпті критерий Z_кр

5. айқын айырмашылықты анықтау

3 есеп

Х1	1,900	2,300	2,500	2,900	3,00
m	1	2	5	7	15

У1	1,900	2,300	2,500	2,900	3,00
n	1	5	4	10	10

Болжау деңгейі P=0,05 . Екі перезентханада туған перезенттердің салмақтарының арасындағы айқын айырмашылықты анықта:

1. Таңдама орташа

2. таңдама дисперсия

3. эксперименталдық (бақылау) критерий Z_экс

4. қауіпті критерий Z_кр

5. айқын айырмашылықты анықтау

Т Е С Т Т Е Р

1. Ситуациялық жорамалды тексеру неше кезеңнен құралады?

1. 5

2. 3

3. 4

4. 6

5. 2

2. Егер Z_экс < Z_кр болса, екі салыстырып отырған жиынтықтың арасында айқын айырмашылық бар ма, жоқпа?

1. Н₀ жорамалды қабылдамайды

2. Алтернативті жорамалды қабылдайды

3. Н₀ жорамалды қабылдайды

4. Алтернативті жорамалды қабылдамайды

5. Н₀ жорамалдың әділдігін кейбір болжау деңгейінде қабылдайды

3. Статистикалық жорамалды тексеруде 1-ші кезеңнің мақсаты

1. Интервалдың көлемін анықтау

2. Нөлдік не алтернативті жорамалды анықтау

3. Салыстырмалы жиілікті анықтау

4. Таңдама орташаны анықтау

5. Орташа квадраттық ауытқуды анықтау

4. Нөлдік жорамалды анықтау үшін қандай мәліметтер қажет?

1. Таңдама орташаны және диперсияны

2. Таңдама дисперсияны және орташа қателік

3. Статистикалық қателік және дисперсия

4. Математикалық күту және таңдама орташа

5. Орташа квадраттық ауытқу және стандарттық қателік

5. Z_кр қауіпті нүктені не үшін анықтайды?

1. Таңдама орташамен салыстыру үшін

2. Орташа дисперсиямен салыстыру үшін

3. Z_экс мәнімен салыстыру үшін

4. Статистикалық қателікпен салыстыру үшін

5. Математикалық күтумен салыстыру үшін

6. Жиынтық арасындағы айқын айырмашылығы бар деген қортынды шығару үшін нені білу қажет?

1. Х және У мәндерін

2. Z_{экс және Д}² мәндерін

3. Z_кр және Х мәндерін

4. Z_{экс және} Z_кр мәндерін

5. _Д² және σ мәндерін

3 Сабақ

Экспериментальдық зерттеуде алынған сандық мәліметтер ретсіз болады. Сол себептен бұл мәліметтер арқылы қортынды шығармаймыз. Сондықтан алғашқы деректерді өңдеу және топтастыру қажет.

Мәліметтерден керек ақпарат алу мақсатымен, алғашқы деректерді жүйелеу процессін топтастыру дейміз.

Интервалдардың санын және енін талдау келесі әдістер арқылы анықталады:

1. Стерджес формуласы: 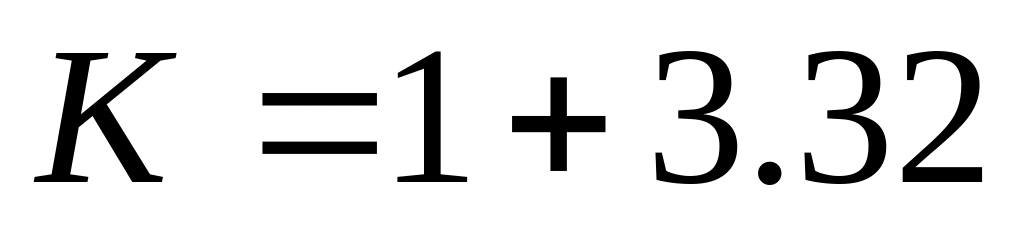lgn

2. N 1 кесте арқылы

3. Топтың интервал санын таңдау.

Таңдама көлемі n	Интервал саны, К
25-40 40-60 60-100 100-200 > 200	5-6 6-8 7-10 8-12 10-15

Интервал енін анықтаймыз

Интервал ені (есеп бойынша)

Ұсақ интервалдан және олардың жиілігінен не салыстырма жиілігінен құралатын қатарды интервалдық қатар дейміз. Интервалдлың бір мөлшеріне келетін жиілікті, жиілік тығыздығы дейміз.

Тік төртбұрыштан құралатын баспалдақ тәрізді фигураны гистограмма дейміз. Кездейсоқ шамалардың таралу сызығының симметриялығын және сүйір ұшының түрін ассиметрия және экцесс коэффициенттері көрсетеді:

Егер = 0 таралу симметрия тәрізді болады.

Егер < 0 таралу кері болады

Таралудың сүйір бұрышының түріне экцесс коэффициенті сипаттама береді.

=

Егер > 0 таралудың сүйір ұшы үшкір болады.

Егер < 0 таралудың сүйір ұшы тегіс тәрізді болады.

№ 1жағдайлық есеп

Интервалдық тарау қатарының мәліметтері бойынша салыстырмалы жиілікті есепте,салыстырма жиіліктің гистограммасын бейнеле.

Х	150-154	154-158	158-162	162-166	166-170	170-174	174-178	178-182	182-186
m	1	2	11	23	25	22	11	3	1
p

№ 2 жағдайлық есеп

Х	25-40	40-60	60-8	80-100	100-120	120-140	140<
m	1	4	20	40	10	5	1
p

Кестеде берілген мәліметтер бойынша салыстырма жиілігін есепте. Салыстырмалы жиіліктің гистограммасын бейнеле.

№ 3 жағдайлық есеп

Емдеу ұзақтығы (күні)Х	3-5	5-8	8-11	11-14	14-17	17-20
m	5	8	15	9	5	3
р

Статистикалық таралу қатарының мәліметтері бойынша салыстырмалы жиілікті есепте. Науқастарды ауруханада емдеу қозғалысы ұзақтығының салыстырмалы жиілігінің гистограммасын бейнеле.

№ 4 жағдайлық есеп

Холециститпен кенеттен ауырғанынан бастап операцияға дейінгі уақыт және операциядан кейінгі асқыну

Уақыты сағатпен Х	До 3	3-5	5-8	8-11	11-14	14-17	17-18	18-20	20-23	23<
Асқыну саны	6	8	12	19	20	24	28	34	38	7-46
р

Интервалдық таралу қатарының мәліметтері бойынша салыстырмалы жиілікті есепте. Салыстырмалы жиіліктің гистограммасын бейнеле.

№5 жағдайлық есеп

Кешенді медициналық қарау өткізгендегі әртүрлі жастағы адамдардың арасындағы созылмалы сырқаттанудың саны.

Х жасы	0-4	4-9	9-14	14-19	19-24	24-29	29-39
m	70	90	98	100	120	150	170
p

Интервалдық таралу қатарының мәліметтері бойынша салыстырмалы жиілікті есепте. Салыстырмалы жиіліктің гистограммасын бейнеле.

№6 жағдайлық есеп

Жарақаттану бойынша әртүрлі жастағы адамдардың дәрігерге қаралу саны.

Жасы Х	0-1	1-3	3-14	14-20	20<
Қаралуға келгендер саны m	10	300	3000	4200	2700
p

Статистикалық таралу қатарының мәліметтері бойынша салыстырмалы жиілікті есепте. Салыстырмалы жиіліктің гистограммасын бейнеле.

Төртінші сабақ

Стьюдент критерий

Тандаманы көлемі аз шамада болса, қалыпты таралған кезделсоқ шамалардың екі бас орташасың салыстыру үшін Стьюдент критерииің қолданады

Тандама бақлауыың нәтижесі бойынша таңдама орташалар Х_в,У_в және дисперсия бағаларың анықталады,сонан кейін t эксперименталдық мәнін формула арқылы есептейміз.

t_экс =

n_x, n_у -X,және У шамалардың тандама көлемдері

t_экс шыққан мәннің t қауапті (Р₁ t)

Стьюдент таралуымен салыстырамыз f = n_x + nу -2

Р айқындылық деңгейі = 0,05

Егер t _экс < t_қау - Н_о қабылдаймыз

Егер t _экс > t_қау - Н_о қабылдамаймыз

Мысал. Бір нақты процедурадан кейінгі 15 науқастың жүрек соғу жиілігі

х	60	65	68	70	72	75	78	80
m	1	1	2	5	3	1	1	1

∑ _m = n =15

X _в =

Бақылау тобына кіретін 15 науқастардың жүрек соғу жиілігі. Бұл топқа ем процедурасы жүргізілмеген

У	60	65	68	70	72	75	78	80
m	1	1	2	5	3	1	1	1

∑ m = n =15

У _в =

Дисперсия бағалар

t_экс=

t_қау

t_экс>t_қау= Н₀ жорамалдарды қабылдамаймыз

Есеп 1

ШҚО туратың 8 жасар 17 балалардың бойларының ұзындығы (см)

116	117	119	120	121	122	123	124
1	1	2	2	4	5	2	1

ОҚО туратын 8 жасар 17 балалардың, бойларының ұзындығы (См)

у	116	117	119	120	121	122	123	124
m	1	2	4	5	3	1	1

Екі салыстырып отырған жиынтықтың арасындағы айқын айырмашылығын аңықта Болжау денгейі Р= 0,05

Есеп 2

25 жастағы 11 жүкті әйелдердің дем алу жиілігі

х	18	19	21	22	23	24	25	26
m	1	1	3	1	2	1	1	1

25 жастағы 11 әйелдердің демалу жиілігі

у	18	19	20	22	23	24	25	26
m	1	1	3	2	1	1	1	1

Екі салыстырып отырған жиынтықтын арасындағы айқын айырмашылығын аңықта. Болжау денгейі Р= 0,0,5

Есеп 3

12 ай ішінде ет комбинаты жұмысшылардың арасындағы өндірістік жарақат саны

х	29	31	37	19	27	41	43	21	35	33	28	36
m	1	1	1	1	1	1	1	1	1	1		1

Тері –жүн комбинатындағы жұмысшылар арасындағы 12 ай ішінде өндірістік жарақат саны.

у	30	32	35	27	25	45	42	43	33	30	28	32
m	1	1	1		1	1	1	1	1	1	1	1

Екі салыстырып отырған жиынтықтын арасындағы айқын айырмашылығын анықта Болжау денгейі Р= 0,05