Алматы энергетика және байланыс институты
Инженерлік кибернетика кафдрасы
БАСҚАРУ НЫСАНДАРДЫ ҮЛГІЛЕУ ЖӘНЕ ИДЕНТИФИКАЦИЯЛАУ
050702 – Автоматтандыру және басқару мамандығы бойынша оқитын студенттер үшін зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар
ҚҰРАСТЫРУШЫ: Ибраева Л.К. Басқару нысандарды үлгілеу және идентификациялау. 050702 – Автоматтандыру және басқару мамандығы бойынша оқитын студенттер үшін зертханалық жұмыстарды орындауға арналған әдістемелік нұсқаулар.– Алматы: АЭжБИ, 2008. – 38 б.
Әдістемелік нұсқаулар «Басқару нысандарды үлгілеу және идентификациялау» пәні бойынша зертханалық жұмыстарды орындауға негізделген. Олар басқару нысандарды үлгілеудің екі негізгі: аналитикалық және тәжірибелік (идентификация) амалдарын қамтиды. Әдістемелік нұсқаулар 7 жұмыстан тұрады. Жұмыстарды орындау үшін (5 жұмыстан басқаларын) MatLab бағдарламалық жүйенің әр түрлі құралдары қолданылады. Бұл жүйе динамикалық жүйелерді практикалық үлгілеуке негізделген жәнеде оның осындай жүйелерді үлгілеп зерттеуге көп деген визуалды құралдары бар. 5 зертханалық жұмыста тәжірибелік нәтижелерді өңдеу үшін «Инженерлік кибернетика» кафедрасында өңделген бағдарлама қолданылады.
Мазмұны
|
|
Кіріспе |
|
1 № 1 зертханалық жұмыс. Сызықты стационарлы жүйелерді зерттеу |
|
1.1 Сызықты динамикалық нысандардың үлгілерінің негізгі түрлері |
|
1.2 Сызықты стационарлы жүйелерді зерттеу |
|
1.3 Зертханалық жұмысты орындауға тапсырма |
|
1.4 Есеп беруге қойылатын талаптар |
|
1.5 Тапсырма варианттары |
|
1.6 Бақылау сұрақтары |
|
2 № 2 зертханалық жұмыс. Жинақталған параметрлері бар нысанды аналитикалық әдістерімен үлгілеу |
|
2.1 Үрдіс бейнелеуі |
|
2.2 Simulink пакетінде жүйелерді үлгілеу |
|
2.3 Үрдіс үлгісін іске асыру |
|
2.4 Зертханалық жұмысты орындауға тапсырма |
|
2.5 Есеп беруге қойылатын талаптар |
|
2.6 Тапсырма варианттары |
|
2.7 Бақылау сұрақтары |
|
3 № 3 зертханалық жұмыс. Резервуардағы сұйықтық деңгейін реттеу нысанның үлгісі |
|
3.1 Нысан бейнелеуі |
|
3.2 Statefiow жүйесі |
|
3.3 Зертханалық жұмысты орындауға тапсырма |
|
3.4 Есеп беруге қойылатын талаптар |
|
3.5 Тапсырма варианттары |
|
3.6 Бақылау сұрақтары |
|
4 № 4 зертханалық жұмыс. Өтпелі функция көмегімен нысанды идентификациялау |
|
4.1 Өтпелі функция көмегімен графикалық идентификациялау әдісі |
|
4.2 Зертханалық жұмысты орындауға тапсырма |
|
4.3 Есеп беруге қойылатын талаптар |
|
4.4 Тапсырма варианттары |
|
4.5 Бақылау сұрақтары |
|
5 №5 зертханалық жұмыс. Сызықты нысанды жиілік сипаттама көмегімен идентификациялау |
|
5.1 Жиілік сипаттама көмегімен беріліс функцияның коэффициенттерін анықтау |
|
5. 2 Өлшеу нәтижелерді өңдеудің бағдарламасы |
|
5.3 Зертханалық жұмысты орындауға тапсырма |
|
5.4 Есеп беруге қойылатын талаптар |
|
5.5 Тапсырма варианттары |
|
5.6 Бақылау сұрақтары |
|
6 № 6 зертханалық жұмыс. Сызықты жүйелерді параметрлік идентификациялау |
|
6.1 Есеп қойылуы |
|
6.2 Параметрлерді идентификациялау |
|
6.3 Үлгіні верификациялау |
|
6.4 Зертханалық жұмысты орындауға тапсырма |
|
6.5 Есеп беруге қойылатын талаптар |
|
6.6 Тапсырма варианттары |
|
6.7 Бақылау сұрақтары |
|
7 № 7 зертханалық жұмыс. Динамиккалық нысандарды параметрлі емес идентификациялау |
|
7.1 Есептің қойылуы |
|
7.2 Дискретті импульсті өтпелі функцияны аппроксимациялау |
|
7.3 Қисықтарды қиыстырып келтіру Curve Fitting Toolbox пакеті |
|
7.4 Зертханалық жұмысты орындауға тапсырма |
|
7.5 Жұмысты орындаудың тәртібі |
|
7.6 Есеп беруге қойылатын талаптар |
|
7.7 Тапсырма варианттары |
|
7.8 Бақылау сұрақтары |
|
Әдебиеттер тізімі |
|
Кіріспе
Математикалық үлгілеу - әр түрлі жүйелер мен құрылғыларда өтетін үрдістерді оларды “нақтылықта” жасамай зертттеудің құралы. Математикалық үлгілерді құрудың екі принципиалды әртүрлі амалдары бар.
Бірінші амал үлгіні таңдағанда зерттелетін процестің жүріс-тұрысын анықтайтын физика-химия заңдарды есепке алуда негізделген. Осындай үлгілер аналитикалық үлгілер деп аталады. Осындай үлгілерді құрастыру табиғаттың фундаменталды заңдарының саны шектелген жәнеде ұқсастық принципі орындалады деген пікірде негізделген, басқа сөзбен айтқанда әр түрлі физикалық маңызы бар өқиғаларды бірдей математикалық тәуелділіктермен бейнелеуге болады. Реттеу нысандардың сипаттамаларын аналитикалық жолмен анықтау олардың дифференциалдық теңдеулерін құрастырумен орындалады. Осы дифференциалды теңдеулер негізгі физикалық заңдылықтарды: масса, энергия және қозғалыс мөлшерлерін сақтау заңдылықтарын қолдану жолмен құрастырылады. Әдетте осы әдіспен нысанның сызықты емес теңдеуін алуға болады, оның аналитикалық шешімі жалпы кезде табылмайды. Келесі қадам – алынған теңдеуді сызықтандыру яғни нысанның сызықты математикалық теңдеуіне көшу. Сызықтандыру белгілі әдіс бойынша бастапқы стационарлы режим аймағында сызықты емес тәуелділіктерді Тейлор қатарына жіктеу жолымен орындалады; жіктеудің тек қана сызықты мүшелері қалдырылып, содан соң статика теңдеуінен алынған теңдеу алынып тасталады. Осы жолмен пайда болған теңдеу бастапқы стационарлы режимнен тек қана кішкене ауытқулар аймағында орындалады.
Екінші амал "қара жәшік" концепциясында негізделген, яғни басқару объектінің ішкі құрамы белгісіз сонымен бірге зерттеушіге керекте емес деп есептелінеді. Барлық ақпарат тек қана нысанды активті немесе пассивті тәжірибеде бақылау жолымен анықталады деп есептейді. Осы жолмен табылған үлгілер эмпирикалық (тәжірибелік) деп аталады. Тәжірибелік үлгілерді құрастырғанда нысанның кірісіндегі және шығысындағы айнымалыларының өндірулері пайдаланылады. Осындай үлгілерді жасау есептері идентификациялау теориясында қарастырылады. Динамикалық сипатамаларды анықтаудың тәжірибелік әдістері үш негізгі топқа бөлінеді: идентификациялаудың тура әдістері, параметрлі және параметрлі емес идентификация.
«Басқару нысандарды үлгілеу және идентификациялау» пәні бойынша ұсынылып отырған зертханалық жұмыстарды орындауға негізделген әдістемелік нұсқаулар 7 жұмыстан тұрады. Осы жұмыстарды орындау үшін MatLab бағдарламалық жүйенің әр түрлі құралдары қолданылады (5 жұмыстан басқалары). Басқа компьютерлік үлгілеу жүйелеріне қарағанда бұл жүйе өзгеше болып табылады. Математикалық есептеулерді автоматтандыру жүйелерінің ішіндегі ең ыңғайлы жүйе және матрицалық операцияларды кеңітіп көрсету мен қолдануда негізделген; осы жағыдай жүйенің атауында да көрінеді MATrix LABoratory (матрицалық лаборатория).
Зертханалық жұмыстарды орындағанда MatLab жүйесінің қажетті болатын құралдарын атап кетейік.
Кез-келген (кейде өте күрделі) есептеулерді тура есептеу режимінде орындауға болады (бұйрық режимінде), басқа сөзбен айтқанда бағдарламаны жазбай. Сондықтан MatLab тек қана қарапайым есептеулерді емес, сонымен бірге векторлармен, матрицалармен, комплексті сандармен, қатарлар және полиномдармен есептеулерді орындайтын өте қуатты ғылыми калькулятор болып табылады. Осы режимдегі жұмыс диалог ортасында орындалады. Сонымен бірге бұйрық терезе MatLab жүйесінің басқа пакеттерінде жұмыс жасағанда қолданылады. Мысалы, әр түрлі пакеттер арасында мәліметтер тікелей емес тек қана бұйрық терезе арқылы тасымалданады. Калькулятор режимінің көп деген мүмкіншілігі болғанмен, күрделі есептерді шешу үшін оларға бағдарламаны өңдеу керек. Процедураларды қолдану үшін пайдаланушы бағдарлама редакторының арнайы терезесінде М-файл-ды жасайды. MatLab жүйенің бұйрық терезесінде жұмыс жасауды және бағдарламалаудың негізгі амалдарын үйрену үшін студент [7] келтірілген 1 және 2 п.п.-ғы жаттығуларды орындауы керек.
1 зерханалық жұмыста сызықты стационарлы жүйелердің үлгілерін жасап анализдеу үшін MatLab жүйесінің бұйрық терезесімен Control System Toolbox пакеті қолданылады. Control Toolbox пакеті автоматты басқару жүйені әр түрлі көз қарас жағынан анализдеуге мүмкіндік береді, соның ішінде біріншіден уақыт және жиілік кеңістіктерінде сыртқы әсерлерге жүйенің реакциясын.
MatLab жүйенің көпшілікке белгілі болушылығына оның қуатты Simulink кеңейтілуі себеп болды. Бұл пакет сызықты және сызықты емес динамикалық жүйелерді блоктық үлгілеу үшін пайдаланушыға ыңғайлы және қарапайым құралдарды ұсынады, соның ішінде визуалды нысанды-бағытталған бағдарламалау құралдарын. 2 және 3 зертханалық жұмыстарда зерттелетін үрдістердің үлгілері Simulink пакетінің блок-диаграммалары ретінде іске асырылып, үлгіні зерттеу визуалды режимде өткізіледі. 4 зертханалық жұмыстада нысанды графикалық әдісімен идентификациялау үшін осы пакет қолданылады.
Жүріс-тұрыстары сыртқы оқиғадан тәуелді жүйелерді үлгілеу MatLab + Simulink жүйесінде Stateflow арнайы кеңейтілуі көмегімен орындалады. Осы пакет 3 зертханалық жұмысты орындағанда қолданылады.
5 зертханалық жұмыста нысанның идентификациясы жиілік сипаттамалар көмегімен «Инженерлік кибернетика» кафедрасында өңделген бағдарлама ортасында орындалады.
Жүйелерді параметрлі идентификациялау үшін (6 зертханалық жұмыс) MatLab бағдарламалық өнімінің графикалық ident ортасы қолданылады.
Жүйелерді параметрлі емес идентификациялау есепетері 7 зертханалық жұмыста қарастырылған. Параметрлі емес идентификациялау есебін сандық шешу үшін жүйенің бұйрық терезесі қолданылады. Ізделінетін импульсті өтпелі функцияның дискретті мәндерін аппроксимациялау үшін қисықтарды қалпына келтіретін Curve Fitting Toolbox пакеті қолданылады.
1 №1 зертханалық жұмыс. Сызықты стационарлы жүйелерді зерттеу
Жұмыс мақсаты: MatLab жүйесінің бұйрық терезесінде динамикалық жүйелердің үлгілерін жасау; үлгілерді Control System Toolbox пакетінің құралдары көмегімен зерттеу.
1.1 Сызықты динамикалық нысандардың үлгілерінің негізгі түрлері
Көп деген жағдайларда сызықты стационарлы жүйенің қарапайым әсерлерге реакциясы оның теориялық сипаттамаларымен анықталады. Солардың негіздері келесілер болып табылады:
- W(p) беріліс функциясы Лаплас L{∙} түрлендіру көмегімен анықталады;
- g(t) импульсты сипаттама – нысанның δ-функция түріндегі кіріс сигналына реакциясы.
Нөлдік бастапқы шарттарда кірудегі және шығудағы сигналдар арасындағы байланыс келесі жыйма интегралымен бейнеленеді
- h(t) өтпелі функциясы – нысанның сатылы функция түріндегі кіріс сигналына реакциясы.
Басқару теориясынан осы сипаттамалар арасында келесідей қатынастар белгілі
L{w(t)}
= W(p), g(t)= h’(t),
;
- нысанның жиілік сипаттамалары, олар комплексті беру коэффициентімен анықталады W(jω)= W(p)|p=jω.
Белгілі түрде көрсетілген нысанның маңызды қасиеттері туралы ақпаратты үлгі деп атаймыз.
Сызықты үздіксіз стационарлы динамикалық нысандардың үлгілерінің негізгі түрлерін келтірейік.
1. Дифференциалды теңдеулер.
Дифференциалды теңдеулерде негізделген ең универсалды үлгі келесі өрнекпен анықталады
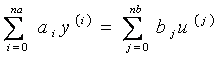
мұнда na – үлгі реті (na >nb);
ai және bj – тұрақты коэффициенттер (үлгі параметрлері);
u(j)(t) және y(i)(t) – кірудегі және шығудағы сигналдарының туындылары.
2. Күй айнымалыларының теңдеулері.
Егер де жүйенің (нысанның) n координаталары xi(t), i=1,2,...,n ретінде оның күйінің айнымалылары таңдалынса (осындай координаталар ретінде, мысалы, шығудағы сигнал y(t) және оның n-1 туындылары болуы мүмкін) берілген жүйені күй айнымалыларының теңдеулерімен келесідей бейнелеуге болады
,
мұнда X(t) = [x1(t), x1(t),..., xn(t)]T - күй айнымалыларының векторы;
скалярлы u(t) және y(t) алдындағы A,B,C және D – nxn өлшемді матрица, nx1x1 өлшемді векторлар және скаляр (u(t) және y(t) векторлар болған кезде, олар – сәйкес өлшемді матрицалар болады).
Келтірілген үлгілер эквивалентті болып табылады, басқа сөзбен айтқанда, біреуін біле отырып қалған барлығын алуға болады.
3. Айырымдық теңдеулер.
Жұмысы дискретті tk=kT уақытта (бұл жерде T – дискреттеу интервалы) өтетін нысандар яғни дискретті нысандар үшін бейнелудің ең жалпы түрі келесі айырымдық теңдеу болады (дифференциалды теңдеудің аналогы)
yk + a1yk-1 + ... + amyk-na = b1uk + b2uk-1 + b3uk-2 + ... + bnbuk-nb+1
мұнда yk-i = y[(k – i)T], uk-j = u[(k – j)T].
4. Z-түрлендіру.
Сигналдар арасындағы байланыс келесі функциялармен көрсетілуі мүмкін:
- дискретті жыйма арқылы
мұнда gi – нысанның салмақ торлы функциясының ординаталары;
- Z-түрлендіруі аппаратын қолданып
мұнда z = e pT;
- дискретті беріліс функция арқылы
,
бұл беріліс функция айрымдық
(1 + a1z-1 + a2z-2 + …+ anaz-na)Y(z) = (b1 + b2z-1 + b3z-2 + …+ bnbz—nb+1)U(z)
теңдеу арқылы, оның екі жағының өрнектеріне Z-түрлендіруді қолданып анықталады.
z-1 = e-pT операторы кідіру операторы болып табылады, яғни
z -1uk = uk-1, z -2uk = uk-2 и т.д.
Практикада көбінесе үздіксіз сигналдарды өлшеу дискретті уақыт моменттерінде өткізілетінін айтып кеткен жөн, ол бір жағынан келешекте мәліметтерді компьютерде өңдеуге ыңғайлы болады. Үздіксіз нысандарды жуықтап дискретті үлгілермен бейнелеуге болады. Сонымен бірге, үздіксіз үлгілерден дискретті үлгілерге көшу үшін Z-түрлендіруді қолданумен, немесе үздіксіз нысанды бейнелейтін дифференциалды теңдеудің туындыларын айырымдық өрнектермен орын басу (бұл жолмен дискреттеу интервалының кіші шамаларында және теңдеудің реті кіші болса ғана керекті дәлдікті алуға болады) жолмен өткізуге болады.
Төменде дискретті нысандардың бір неше көп тараған бақылау шуларын есепке алатын уақыт аймағындағы дискретті үлгілері келтірілген (дискретті уақыттың t моменттері үздіксіз уақыттың белгісімен белгіленген t = 0, 1, 2…).