Определени вторичных и первичных параметров из опытов холостого хода и короткого замыкания
Дана линия, о которой ничего не известно. Нам предоставлены зажимы, известно, что
(2.13)
Отсюда можно найти волновое сопротивление линии
(2.14)
и коэффициент распространения
(2.15)
Считаем, что известна частота и длина линии, тогда можно записать
,
.
Отсюда можно найти первичные параметры линии
.
(2.16)
При определении возникает неоднозначность.
13. Свойства отрезка линии длиной /4
Рассмотрим линию длиной кратной четверти длины волны /4. Ее длина равна
(*)
Запишем волновое сопротивление линии в следующем виде:
.
(2.17)
Будем предполагать, что выбранный нами отрезок обладает малым затуханием, то есть l – мало, тогда
Подставим l в выражение и получим
(2.18)
Отрезок линии длиной /4 обладает трансформирующим свойством (пересчитывает нагрузку к выходу).
В исходной линии волновое сопротивление не равно сопротивлению нагрузки ZB ZH.
Поэтому
чтобы согласовать линию, включаем новую
линию длиной /4,
подбирая конструктивно
.
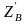Трансформирующая линия должна иметь волновое сопротивление
(2.19)
Рис. 1.1.13 Трансформирующая линия
Более подробно рассмотрим свойства линии длиной /4, обратимся к выражению.
Короткозамкнутая четверть волновая линия.
Рис. 1.1.14 Схема короткозамкнутой линии длиной /4
Сопротивление
нагрузки равно нулю
,
тогда
,
т.е. четвертьволновый, замкнутый на
конце отрезок действует как «металлический
изолятор». Он эквивалентен параллельному
колебательному контуру с очень высокой
добротностью порядка
.
Т
олько
в отличие от настоящего резонансного
контура он имеет не одну, а много
резонансных частот. Резонанс наступает
каждый раз, как только выполняется
соотношение (*).
Рис. 1.1.15 Практическое использование свойств четвертьволновой линии
Практически все это можно использовать при длине волны в дециметровом, сантиметровом и миллиметровом диапазоне.
Свойства полуволновых отрезков линии
Рассмотрим линию длиной кратной половине длины волны /2. Ее длина равна
Для такой линии справедливы следующие соотношения:
Входное сопротивление полуволновой линии будет равно
(2.14)
У такой линии на входе видим то, что включено на выходе. Такой отрезок ведет себя как последовательный колебательный контур с добротностью (многорезонансный) .