1. Искажения в линиях передачи.

Для того, чтобы не было амплитудно-частотных искажений необходимо, чтобы коэффициент не зависел от частоты.

Рис 1.1.1 График изменения  от частоты

Вспомним, что коэффициент распространения равен

(1.1)

Чтобы не было фазо-частотных искажений необходимо, чтобы время запаздывания не зависели от частоты, т.е

где β – линейная функция частоты

(1.2)

Докажем, что если выполнено условие Хевисайда, то искажений не будет.

Из условия Хевисайда имеем

.

Подставив значение индуктивности L в выражение, получим

или

, (1.3)

отсюда, видим, что , а

Таким образом, при соблюдении условия Хевисайда коэффициент  от частоты  не зависит, а коэффициент  является линейной функцией частоты  . Время запаздывания равное

.

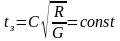Возникает вопрос: выполняется ли условие Хевисайда для реальной линии? Ответ на этот вопрос – нет.

Это на самом деле так, так как для реальной линии

(1.4)

Чтобы выполнить условие Хевисайда можно включить дополнительные индуктивности в разрыв линии через определенные расстояния.

(1.5)

Выполнение условия Хевисайда не только устраняет искажения, но и минимизирует затухания.

Включение дополнительных катушек с целью уменьшения затухания и устранения искажений называется пупинизацией.

В настоящие время оно используется редко.

2. Волновое сопротивление линии

К вторичным параметрам линии относится также волновое сопротивление, которое может быть найдено по закону Ома, как отношение волны напряжения в любой точке линии к току

.

Запишем условие согласования линии

(1.6)

Характер волнового сопротивления Z_В говорит о характере энергии, переносимой вдоль линии:

.

Изменение модуля волнового сопротивления не характеризует прямо изменение потерь энергии в линии. Волновое сопротивление может повысится, как при увеличении Z_пр, так и при уменьшении Y_из.

.

, (1.7)

(1.8) Нарисуем зависимости

Рис. 1.1.2 Графики зависимостей

3. Коэффициент отражения

При проведении расчетов линии удобно пользоваться коэффициентом отражения , который равен отношению отраженной волны напряжения (или тока) к падающей волне напряжения (или тока, соответственно).

(1.9)

Рассмотрим несколько ситуаций.

1. Отраженной волны нет, линия включена согласованно (z_Н= z_В).

2. Волна напряжения в конце линии отражается в той же фазе. Волна тока – в противофазе. Результирующее напряжение в конце линии удваивается, а результирующий ток равен нулю. Имеем опыт холостого хода (z_н ).

3. Волна напряжения в конце линии отражается в противофазе. Волна тока – в фазе. Результирующий ток в конце линии удваивается, а результирующее напряжение равно нулю. Имеем опыт короткого замыкания (z_н = 0).

Коэффициент отражения показывает соотношение между параметрами линии и нагрузки.

(1.10)

Формулу можно доказать, используя систему:

Пусть x = l , тогда имеем

.

Выражая напряжение через токи и сопротивления нагрузки и волновое соответственно, получаем

Если из первого уравнения вычесть второе, то можно получить формулу, то есть

,

что и требовалось доказать.