- •4.3. Указание к выбору коэффициентов управления
- •4.4. Указания к выбору начальных условий
- •4.5. Указания к составлению уравнений, описывающих изменение углов поворота и угловых скоростей звеньев
- •4.6. Указания к численному решению задачи
- •4.7. Контроль решения
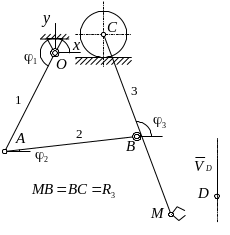
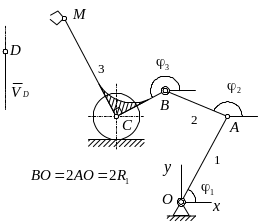
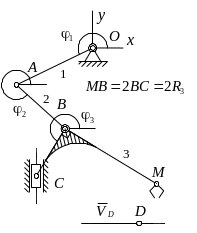
- •5. Пример выполнения задания (Вариант 37, , )
- •5.1. Составление уравнений движения
- •5.2. Определение параметра управления
- •5.2. Решение задачи на эвм и обработка результатов
- •5.3. Контроль решения
- •6. Содержание отчета о работе
- •7. Контрольные вопросы:
- •8. Литература
6. Содержание отчета о работе
Отчет должен содержать;
- титульный лист с указанием названия работы, фамилии исполнителей и преподавателя;
- номер варианта и содержание задания;
- листинг программы решения задания;
- выводы по работе.
7. Контрольные вопросы:
1. Как изменится решение задачи, если точка М будет двигаться по произвольно заданной кривой?
2. Почему множитель имеет размерность времени?
3. Как следует выбирать величину при изменении требований на точность сближения точек M и D.
4. Дайте характеристику различным способам управления траекторией движения рабочих органов робота: управление па вектору скорости, по вектору силы, управление по методам последовательных корректировок положения, линейного программирования движения, динамического программирования и др.
Листинг 1
function kinematik
R1 = 0.953; R2 = 0.847; R3 = 0.457; Vd = 0.304; dt = 0.057; Tc = 0.297;
delta = 0.01; fi10 = 1.63; fi20 = 3.37; fi30 = 2.87;
Xd0 = -2.15; Yd0 = 1.18; alf = 4.35;
Xd = Xd0; Yd = Yd0; fi1 = fi10; fi2 = fi20; fi3 = fi30;
[Xm0,Ym0] = get_Xm_Ym(R1,R2,R3,fi10,fi20,fi30);
Xm = Xm0; Ym = Ym0; Vdx = Vd*cos(alf); Vdy = Vd*sin(alf); dR = 1; i=1; t=0;
while (dR > delta),
[Vmx,Vmy] = get_Vmx_Vmy(Xm,Ym,Xd0,Yd0,Vdx,Vdy,Tc,t);
[w1,w2,w3,Vcx] = get_w1_w2_w3_Vcx(R1,R2,R3,fi1,fi2,fi3,Vmx,Vmy);
XmV(i) = Xm; YmV(i) = Ym; XdV(i) = Xd; YdV(i) = Yd;
VcxV(i) = Vcx; VmxV(i) = Vmx; VmyV(i) = Vmy;
tV(i) = t; w1V(i) = w1; w2V(i) = w2; w3V(i) = w3;
fi1V(i) = fi1; fi2V(i) = fi2; fi3V(i) = fi3;
Xm = Xm + Vmx*dt; Ym = Ym + Vmy*dt; Xd = Xd + Vdx*dt; Yd = Yd + Vdy*dt;
fi1 = fi1 + w1*dt; fi2 = fi2 + w2*dt; fi3 = fi3 + w3*dt;
t = t + dt; i=i+1; dR = sqrt((Xm - Xd)^2+(Ym - Yd)^2);
end;
plot(tV,VcxV,'k'); plot(tV,w1V,'k--',tV,fi1V,'k');
plot(tV,w2V,'k--',tV,fi2V,'k'); plot(tV,w3V,'k--',tV,fi3V,'k');
plot(XmV,YmV,'k:',XdV,YdV,'k-.',Xd0 ,Yd0,'kv',XmV(1),YmV(1),'ko', XmV(length(YmV)),YmV(length(YmV)),'ko',XdV(length(XdV)),YdV(length(XdV)),'kv');
function [Xm, Ym] = get_Xm_Ym(R1,R2,R3,fi1,fi2,fi3)
Xm = R1*cos(fi1) + R2*cos(fi2) + 2*R3*cos(fi3);
Ym = R1*sin(fi1) + R2*sin(fi2) + 2*R3*sin(fi3);
function [Vmx,Vmy] = get_Vmx_Vmy(Xm,Ym,Xd0,Yd0,Vdx,Vdy,Tc,t)
Vmx = Vdx + (Xd0 + Vdx*t - Xm)/Tc;
Vmy = Vdy + (Yd0 + Vdy*t - Ym)/Tc;
function [w1,w2,w3,Vcx] = get_w1_w2_w3_Vcx(r1,r2,r3,fi1,fi2,fi3,Vmx,Vmy)
w3 = Vmy/(r3*( 2*cos(fi3) + sin(fi3) ));
Vcx = Vmx + w3*r3*( 2*sin(fi3) - cos(fi3));
w1 = (Vcx*cos(fi2) + w3*r3*cos(fi3-fi2))/(r1*sin(fi2-fi1));
w2 = (w3*r3*sin(fi3) - w1*r1*cos(fi1))/(r2*cos(fi2));
8. Литература
Основная
Промышленная робототехника / Л.С .Ямпольский, В.А. Якимович, Е.Г. Вайсман и др.; Под. ред. Л.С .Ямпольского. – Киев: Техника, 1984.
Робототехника и гибкие автоматизированные производства/ Под. ред. И.М. Макарова. Кн.3. Управление робототехническими системами и ГАП. – М.: ВШ, 1986.
Медведев В.С., Лесков А.Г., Ющенко А.С. Системы управления манипуляционными роботами. – М.: Наука, 1978.
Дополнительная
Яблонский А.А., Никифорова В.М. Курс теоретической механики. – Ч.I,: М.: Наука, 1984.
Васильева А.В., Бутузов В.Ф. Асимптотическое разложение решений сингулярно-возмущенных уравнений.- М.: Наука, 1973.
Приложение 1
Вариант |
|
|
|
|
|
|
|
|
|
|
1 |
0.82 |
0.68 |
0.46 |
2.9 |
1.1 |
0.5 |
0.508 |
-0.15 |
1.85 |
0.011 |
2 |
0.81 |
0.47 |
0.91 |
1.3 |
2.2 |
3.6 |
0.308 |
-0.94 |
1.71 |
0.012 |
3 |
0.43 |
0.91 |
0.84 |
0.3 |
3.8 |
4.2 |
0.512 |
-0.42 |
0.25 |
0.013 |
4 |
0.42 |
0.97 |
0.88 |
2.8 |
0.2 |
5.7 |
0.462 |
-0.21 |
1.22 |
0.014 |
5 |
0.78 |
0.45 |
0.81 |
1.7 |
0.1 |
5.8 |
0.385 |
1.35 |
1.51 |
0.015 |
6 |
0.71 |
0.89 |
0.76 |
4.6 |
0.1 |
1.6 |
0.312 |
1.33 |
-1.20 |
0.016 |
7 |
0.46 |
0.97 |
0.74 |
1.3 |
4.3 |
5.6 |
0.421 |
-0.61 |
-0.24 |
0.017 |
8 |
0.81 |
0.72 |
0.48 |
1.1 |
3.0 |
3.3 |
0.472 |
-1.38 |
1.61 |
0.018 |
9 |
0.76 |
0.79 |
0.45 |
0.3 |
2.4 |
1.8 |
0.465 |
0.54 |
1.02 |
0.019 |
10 |
0.72 |
0.49 |
0.78 |
0.5 |
4.2 |
3.6 |
0.375 |
1.61 |
-0.55 |
0.020 |
11 |
0.83 |
0.57 |
0.49 |
0.5 |
1.6 |
3.0 |
0.525 |
-0.92 |
1.78 |
0.021 |
12 |
0.68 |
0.46 |
0.83 |
3.9 |
4.9 |
0.3 |
0.310 |
0.46 |
-2.04 |
0.022 |
13 |
0.78 |
0.85 |
0.49 |
2.1 |
1.0 |
0.1 |
0.460 |
0.51 |
1.65 |
0.023 |
14 |
0.48 |
0.97 |
0.73 |
0.3 |
1.8 |
3.7 |
0.402 |
0.26 |
1.30 |
0.024 |
15 |
0.42 |
0.97 |
0.78 |
0.3 |
2.9 |
0.4 |
0.455 |
0.45 |
1.12 |
0.025 |
16 |
0.51 |
0.82 |
0.79 |
3.2 |
4.1 |
3.0 |
0.288 |
-1.57 |
0.13 |
0.026 |
17 |
0.41 |
0.83 |
0.98 |
2.0 |
4.3 |
1.4 |
0.451 |
-1.18 |
0.56 |
0.027 |
18 |
0.82 |
0.45 |
0.78 |
1.6 |
2.9 |
0.4 |
0.312 |
-0.99 |
0.52 |
0.028 |
19 |
0.92 |
0.98 |
0.81 |
1.5 |
2.7 |
1.7 |
0.294 |
-1.43 |
1.95 |
0.029 |
20 |
0.79 |
0.68 |
0.48 |
4.1 |
5.8 |
1.1 |
0.306 |
0.41 |
-1.43 |
0.030 |
21 |
0.76 |
0.42 |
0.85 |
5.2 |
0.4 |
2.3 |
0.380 |
0.84 |
0.26 |
0.031 |
22 |
0.75 |
0.78 |
0.47 |
1.1 |
2.8 |
2.0 |
0.515 |
-1.66 |
0.42 |
0.032 |
23 |
0.71 |
0.49 |
0.82 |
4.9 |
0.1 |
1.9 |
0.385 |
0.62 |
0.12 |
0.033 |
24 |
0.75 |
0.6 |
0.78 |
0.3 |
1.9 |
0.1 |
0.398 |
1.11 |
1.32 |
0.034 |
25 |
0.68 |
0.79 |
0.82 |
2.3 |
0.7 |
0.5 |
0.392 |
1.40 |
1.67 |
0.035 |
26 |
0.81 |
0.72 |
0.49 |
3.7 |
5.4 |
4.2 |
0.371 |
0.13 |
-1.98 |
0.036 |
27 |
0.78 |
0.65 |
0.48 |
1.6 |
0.1 |
1.5 |
0.275 |
0.31 |
1.62 |
0.037 |
28 |
0.45 |
0.97 |
0.78 |
0.9 |
0.5 |
3.9 |
0.290 |
1.22 |
0.78 |
0.038 |
29 |
0.49 |
0.98 |
0.77 |
2.1 |
0.4 |
3.7 |
0.305 |
0.21 |
0.72 |
0.039 |
30 |
0.72 |
0.75 |
0.49 |
3.9 |
5.4 |
0.3 |
0.340 |
1.14 |
-1.25 |
0.040 |
Приложение 2
1
2 |
|
3 |
|
4 |
5
8 |
6 |
|
7
|
|
9 |
|
10
11 |
|
12 |
|
13 |
14
15 |
|
|
16
17 |
|
18 |
|
|
19
20 |
21 |
|
22
|
23 |
24 |
|
25 |
26 |
27 |
|
28 |
29 |
30 |
|
Приложение 3
Некоторые функции визуализации двумерной и трехмерной графики системы Matlab.
Двумерные графики |
|
PLOT |
график в линейном масштабе |
LOGLOG |
график в логарифмическом масштабе |
SEMILOGX |
график в полулогарифмическом масштабе |
Трехмерные графики |
|
PLOT3 |
построение линий и точек в трехмерном пространстве |
MESHGRID |
формирование двумерных массивов X и Y |
MESH, MESHC, MESHZ |
трехмерная сетчатая поверхность |
SURF, SURFC |
затененная сетчатая поверхность |
SURFL |
затененная поверхность с подсветкой |
AXIS |
масштабирование осей и вывод на экран |
GRID |
нанесение сетки |
HOLD |
управление режимом сохранения текущего графического окна |
SUBPLOT |
разбиение графического окна |
ZOOM |
управление масштабом графика |
SHADING |
затенение поверхностей |
CONTOURC |
формирование массива описания линий уровня |
CONTOUR |
изображение линий уровня для трехмерной поверхности |
CONTOUR3 |
изображение трехмерных линий уровня |
Надписи и пояснения к графикам |
|
TITLE |
заголовки для двух- и трехмерных графиков |
XLABEL, YLABEL |
обозначение осей |
LEGEND |
пояснение к графику |
TEXT |
добавление к текущему графику текста |